The Principle of Least Action
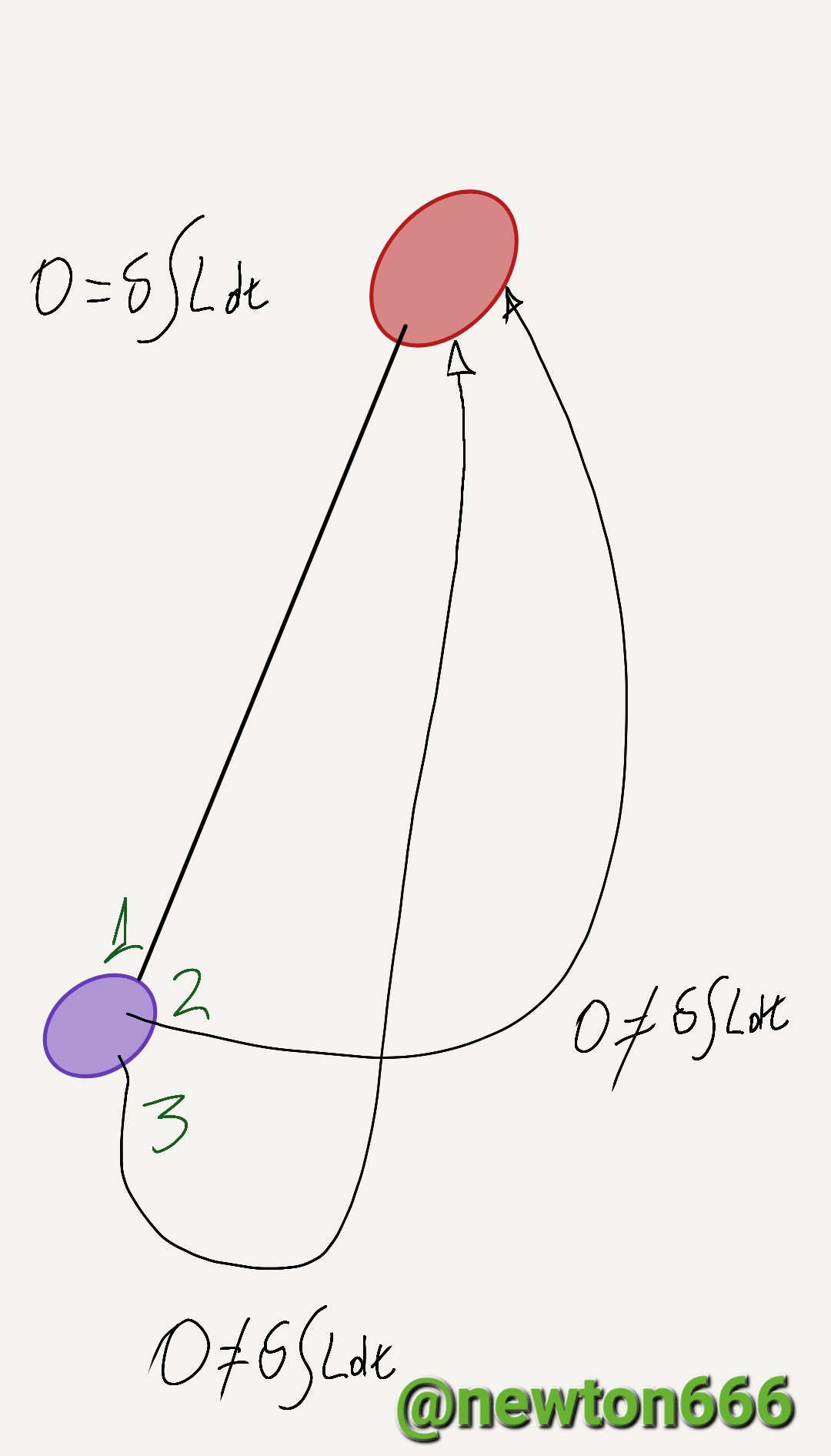
Red electrons are costs, blue electrons are free, all paths are visible because the strategy guarantees that path 1 (the best path) is chosen.
The origins of the principle of inferiority date back to the 17th century, when Pierre de Fermat developed the least important method of analysis and the concept of analysis. Fermat said that light travels along a path that minimizes its travel time. This is the first way of thinking that nature follows a path that minimizes the amount of other things. However, it was Leonhard Euler who, in the 18th century, began to develop a more general formulation of the principle. Euler introduced the concept of "action", which is a quantity that combines energy and time, and postulated that the path followed by a physical system is one for which the action is stationary. This idea lay dormant for many years until it was reformulated and refined by other notable physicists such as Joseph-Louis Lagrange and William Rowan Hamilton.
The mathematical formulation of the minimum operating principle is beautiful and powerful. This depends on the reaction, represented by the letter S, which is important in the space-time direction. The action of a particle is defined as the Lagrangian integral (L), along its path from an initial point (t1), to an end point (t2):
S = ∫ t1t2 L(q, q´, t) dt
Where:
- S is the action.
- L is the Lagrangian, which is a function that depends on the generalized coordinates (q) of the particle, its derivatives with respect to time q', and time (t).
- ∫ t1t2 denotes the integral along the path from t1 to t2.
According to the principle of minimum work, the direct path that physical activity follows is the path of constant or lesser work, expressed mathematically as:
δS = 0
From this equation the Lagrangian is derived. Equations of motion, which describe the behavior of a system in terms of coordinates and their derivatives.
Importance and applications
The principle of inertia is important in physics because it connects and unifies various physical phenomena. Some of the most common are:
1. Classical Mechanics: In classical mechanics, the reduction principle is used to derive Lagrange's equations, which are a very powerful and illustrative approximation to Newton's laws.
2. Optics: Fermat's principle is a special case of the principle of least action and is used to explain the propagation of light in various media.
3. Quantum Mechanics: In quantum mechanics, this function is used to create the minimum of the Schrödinger wave function, which describes the evolution of quantum particles.
4. Field Theory: In field theory, the principle of least action is used to find the equations of motion of a moving field, such as an electric field.
.
The zero principle is a key concept in physics that has proven to be very powerful and effective in explaining and predicting various physical phenomena. Its beauty lies in its ability to combine and simplify the laws of nature through beautiful design and mathematics, thus becoming an important pillar in our understanding of nature and our environment.
Bibliographic Reference
Classical field theory by L. D. Landau, E. M. Lifshitz, V. B. Berestetskii, 2021.
Electromagnetic Interaction. Classical Theory by Joan Costa Quintana, Fernando López Aguilar, 2007.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.