A particle moving along a straight line

Suppose you have a particle moving along a straight line, and its position in time is given by the function s(t) = 2t^2 - 3t + 1, where s(t) represents the position in meters and (t) is the time in seconds.

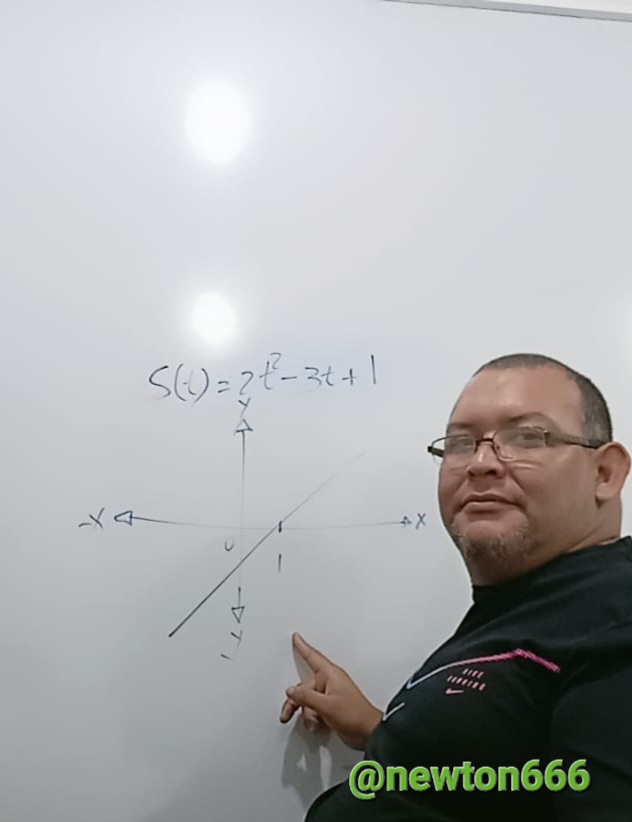
1. Find the speed of the particle as a function of time.

2. Calculate the average speed of the particle in the time interval 1 ≤ t ≤ 3.

3. Determine the acceleration of the particle as a function of time.

Solution:

1. To find the speed of the particle, we take the derivative of the function s(t), with respect to time (t):

v(t) = ds/dt = ds/dt(2t^2 - 3t + 1)

v(t) = 4t - 3

So the speed of the particle as a function of time is v(t) = 4t - 3 meters per second.

2. To calculate the average speed in the time interval 1≤ t ≤3 we can use the formula:

Vavg = Δs/Δt

Where Δs is the change in position and Δt is the change in time. In this case:

Δs = s(3) - s(1) = (2(3)^2 - 3(3) + 1) - (2(1)^2 - 3(1) + 1) = (18 - 9 + 1 ) - (2 - 3 + 1) = 10 - 0 = 10 meters

Δt = 3 - 1 = 2 seconds

Vaverage = 10/2 = 5 meters/second

Therefore, the average speed in the time interval 1 ≤ t ≤ 3 is 5 meters/second.

3. The acceleration of the particle is obtained by taking the derivative of the velocity with respect to time:

a(t) = dv/dt = d/dt (4t - 3)

a(t) = 4

The speed of the particles as a function of time is (t) = 4) meters per second. This means that the speed of the particle in the positive direction is 4 m/s².

Scientific analysis:

This exercise shows how mathematics is used in physics to describe and analyze the movement of particles over time. The following is a scientific analysis of each phase function:

Velocity of the particle: The velocity of the particle is determined by differentiating the function s(t) with respect to time (t) and giving the instantaneous velocity v. (t). In this case the speed is a function of (t) with the symbol v (t) = 4t - 3.

This means that the speed of the particle changes with time and the coefficient 4 represents the speed. With an increase of 4 m/s for each passing second, the real term (-3) means that the initial velocity of the particle at time (t = 0) is (-3) m/s.

Average velocity: The average velocity during time 1 ≤ t ≤ 3 is calculated as the change in position Δs during that time divided by the change in time Δt. In this case, the average speed is 5 meters per minute. This means that during this period the particles move at an average speed of 5 m/s.

Acceleration of particles: Acceleration of particles is obtained by taking the percentage of velocity v (t) and time (t), i.e. acceleration of (t). In this case the speed is the same with a value of 4 meters per second squared and (t) = 4 which means that the particle moves faster which means that its speed increases by 4 m/s.

How to use calculus to analyze the motion of particles, that is, changes in position, velocity, and acceleration over time. These principles are important in physics for understanding and predicting motion, and they are also important for solving real-life motion problems.

Bibliographic Reference

General physics by Santiago Burbano de Ercilla, 2003.

Engineering Mechanics: Dynamics by R. C. Hibbeler, 2004.