Finding The Length Of an Angle Bisector of a Triangle (2nd part)

Hello math bugs(🐞) and hivers(🐝)
Well come to my math blog

Today I have come up with the second part of Finding Angle Bisector of Triangle when three sdies of a triangle are given. But if you want to get it using sine rule we need to the angle also.

In my previous post I did prove that AD in the following figure can be given by [AB × AC - BD × CD]. Check it here.

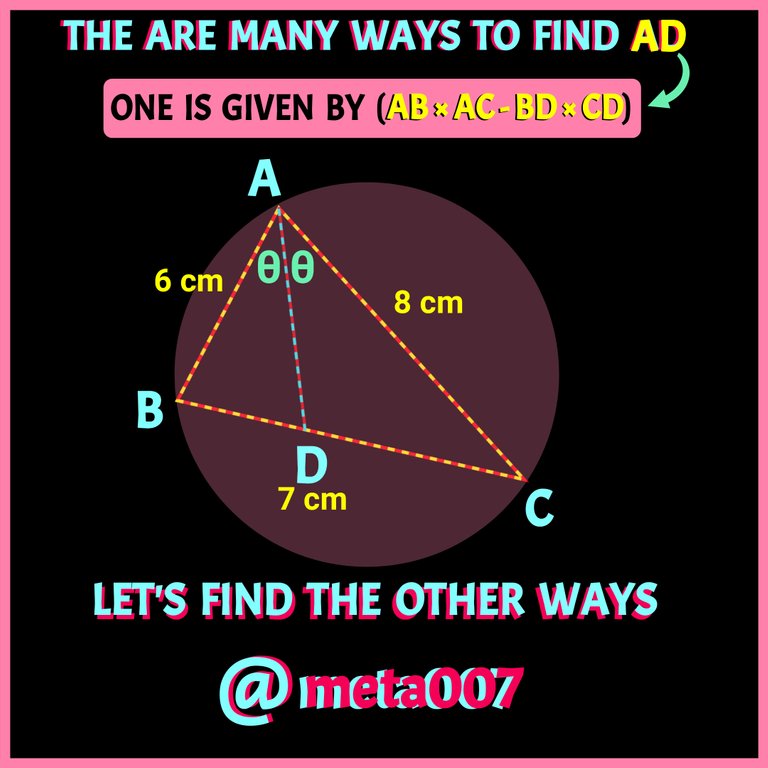
Previously we found AD = 6 cm. Now, let's try to find the other apporaches.

Using Sine Rule:

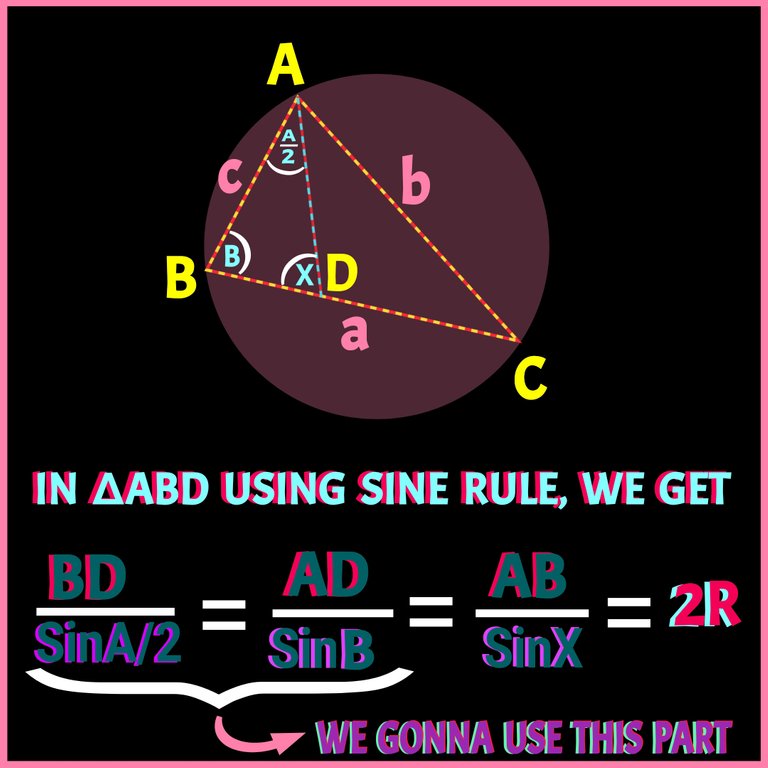
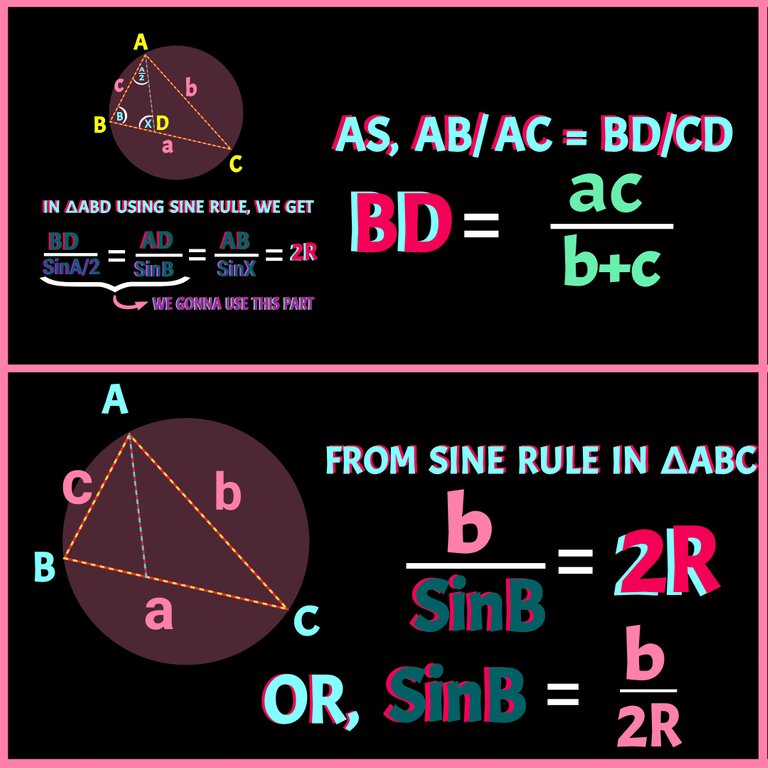
Check details of Sine Rule

A trogonometeic formulla is used to make ∠A half. This is given by Sin(2A) = 2SinACosA or
SinA = 2Sin(A/2).Cos(A/2).
You can search on Google "Sin2A".

To Use this method we should have given Two sides & the angle between them and we can find the length of the bisector of the given angles.

Using Cosine Rule:

You can check details of Cosine Rule in my previous post. This time, it will be easier once you got the cosine rule. Check the figure below 👇

Now using cosine rule in ∆ABD and ∆ADC , we can write as follows.

We already know BD = m = ac/(b+c) =3 cm and CD =n = ab/(b+c) = 4 cm If we put value of b, c, m and n im the above equation, we can have x²= 36. So, x = AD = 6 [cm]

Finding AD using Stewart's Theoream:

The gemetric formullae I used before, had aleadey been proved except the trigonometric one. Now I am gonna proof stewart's law which is written as follows CD(AB)² + BD(AC)² = BC(AD² +BD×CD).

For easier calculation I'll consider the following figure.

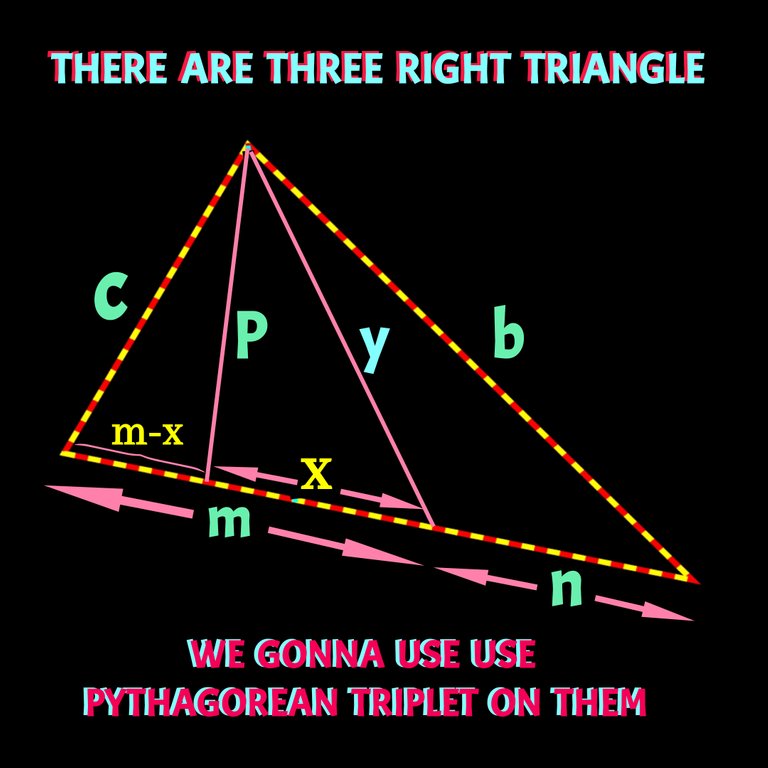
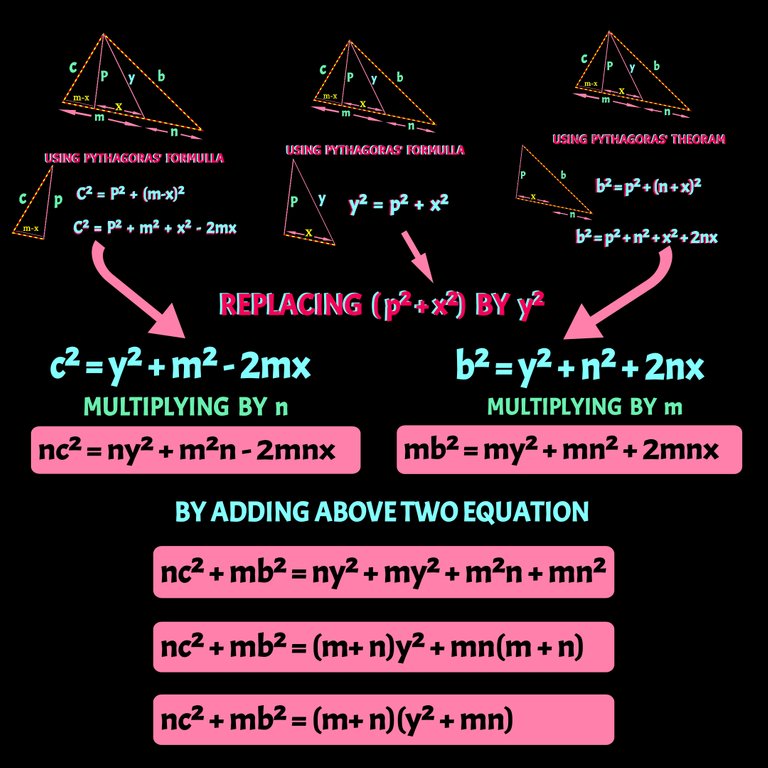
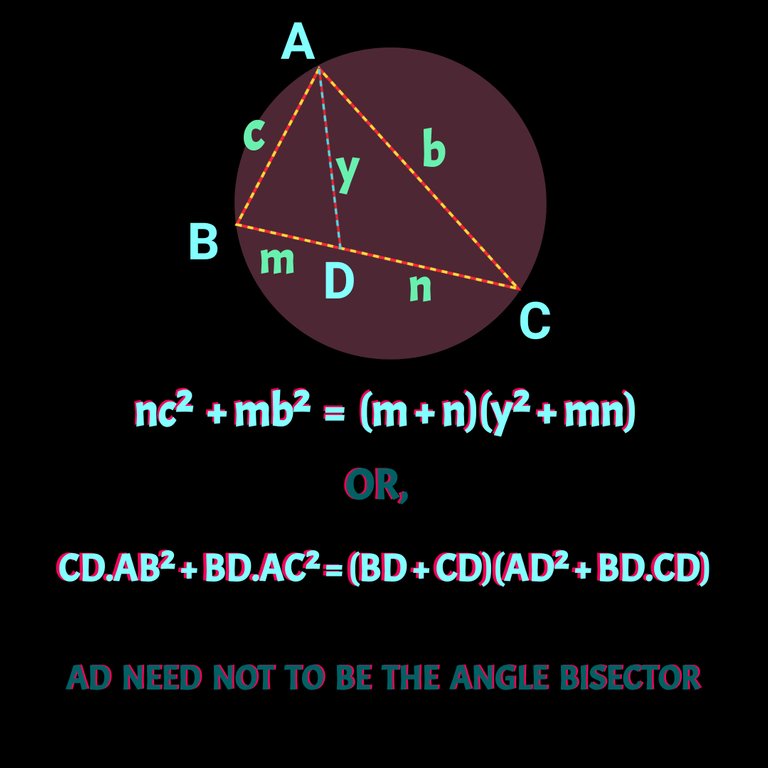
We know all the values except, the bisector AD. If put all the values in stewart theoream proved above, we can easily find out AD. You may be worried about the value of BD and CD. I have mentioned about it earlier right before started proving this theoram.

I have a very hard time framing all those figures. If there be any silly mistakes, please try to ignore it.I hope you like my work.

Thank you so much for stoping by.

Have a nice day.

All is well.

@enforcer48 , here are the other ways.

Regards: @meta007