Another interesting problem related to circle and triangle

Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout and doing good in life

You can see a ∆ABC circumscribed by a circle. CD and BE , the bisectors of ∠ABC do touch the cir-cum-circle at D and E respectively. If ∠BAC be 50° and ∠BED be 30°, you need to find ∠CDE. Check the figure 👇

As there is a cir-cum-circle touches the three vertices of the ∆ABC, it might seem that we have to deal with concept of circ-cum-cricle but Let me tell you , there is mothing to do with cir-cum-cicle. It's just to get the points D and E on it.

The problem becomes rather simple if you konw about in-cricle of a triangle and its relation Between angle(s) of the triangle on whcih it is circumscribed. This was a little hint. Now you can try it once.

The concepts/ postulates/ axioms needed to solve it:

✅ When two or three angle bisectors of a triangle are drawn vertices of a triangle, they always meet at point called incentre. Here bisectors CD and BE meet at a point whcih is called incentre. Let's call the poin I. We need to find ∠BIC. And ∠BIC is given by (90° + half∠BAC).Check it below

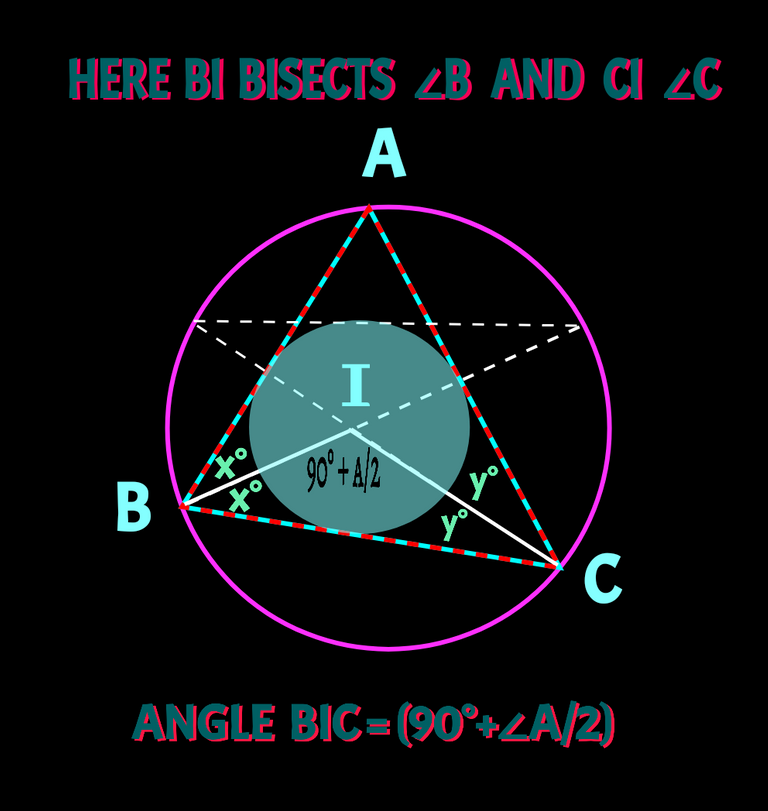
I am not going to discuss how it comes. I did it in my previous posts. Check details of in-circle / in-centre and how ∠BIC equal to (90°-A/2) is here

✅✅ Secondly we need to know that when two line segments touch each other, the vertically opposite angle become equal. Check 👇

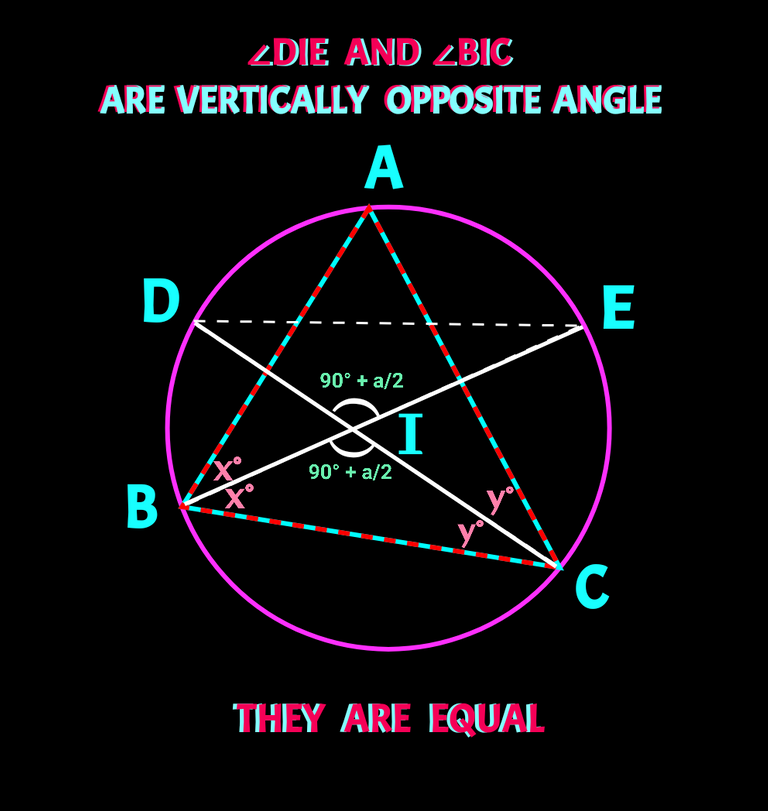
✅✅✅ We need to know that sum of three angles of a triangle is equal to 180°. The most simple one!! I think there is no need to draw a picture.

Solution:

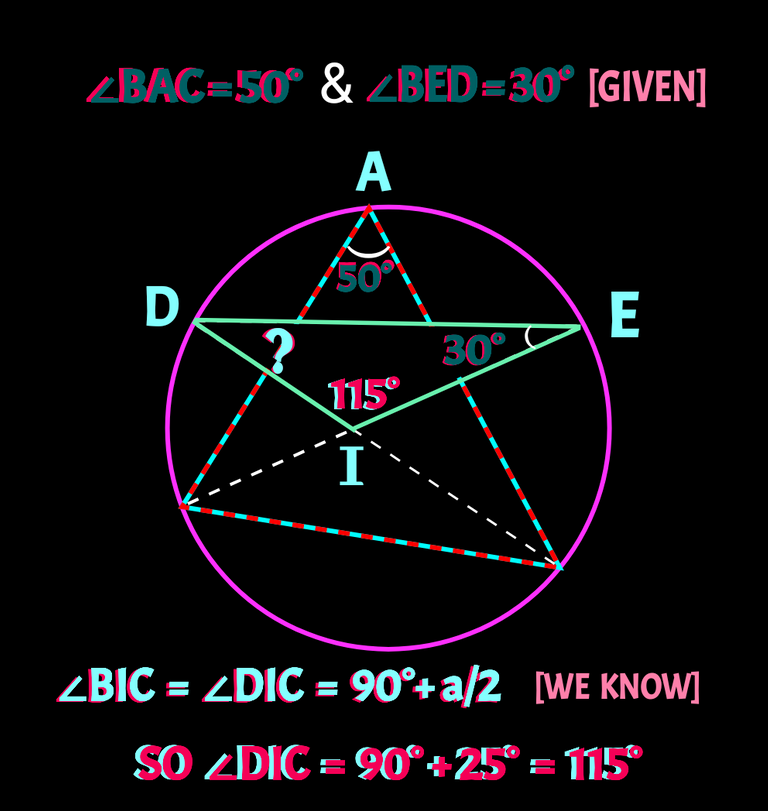
We have been given ∠BAC = 50° and ∠BED = 30° and we have calculated the value of ∠DIE = 115°

          So, ∠CDE or ∠IDE   

         = 180° - (30° + 115°)

         = (180° - 145°) 

         = 35°

All the figures are made by me using android application. Please try avouding silly simtakes and try to consider the given data only.

I hope you liked my today's work.

Thanks for visiting

All is well

Regards: @meta007