Infinite Sequences and Series: The Integral Test and Estimate of Sums
In this video, I go over further into Infinite Sequences and Series and this time look at The Integral Test and Estimating Sums. Often times it is not easy or even possible to formulate a simple function for the n-th partial sum, thus making it very difficult to directly compute the total sum of the series. Thus, other methods are required to first determine if a given series will converge or diverge but without having to do deal directly with the series. I go over one such method, The Integral Test, which geometrically shows that if a series can be written as a function of x and it is decreasing and continuous as x gets large, then the divergence or convergence of the integral of the function itself (i.e. the area under the curve) correlates to the divergence or convergence of the series. A similar approach is shown for estimating the value of a convergent sum and involves considering the minimum and maximum bounds of the remainder in terms of the area or integral of the function as well. This is another in-depth dive into infinite sequences and series so hope you enjoy!
The topics and sections covered in this video are listed below with their timestamps:
- @ 1:30 - Introduction to The Integral Test and Estimate of Sums
- @ 22:20 - The Integral Test
- @ 27:39 - Example 1
- @ 37-20 - Example 2: P-Series
- @44:06 - Theorem 1: P-Series
- @44:35 - Example 3
- @ 46:56 - Example 4
- @ 1:00:27 - Estimating the Sum of a Series
- @ 1:06:46 - Theorem 2: Remainder Estimate for the Integral Test
- @1:08:58 - Example 5
- @1:20:12 - Theorem 3
- @ 1:21:59 - Example 6
- @ 1:29:31 - Proof of the Integral Test
- 3Speak: https://3speak.tv/watch?v=mes/vzgfttzl
- Odysee: https://odysee.com/@mes:8/infinite-sequences-and-series-the:9
- BitChute: https://www.bitchute.com/video/4e41L1QWqvI5/
- Rumble: https://rumble.com/v1znbb8-infinite-sequences-and-series-the-integral-test-and-estimate-of-sums.html
- DTube: https://d.tube/#!/v/mes/QmSPsLMSipMJe2rRrP9bx5kFBzinBnVy6tNr2HZds3Btx2
- YouTube: https://youtu.be/geCSM3vm6eI
Download Video Notes:
- PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIh-81BgKD2GACAGwsDA
- Excel File: https://1drv.ms/x/s!As32ynv0LoaIh-wyl_SMrkmlNx1E2Q
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://peakd.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
- See Part 6 for my Self Appointed PhD and #MESDuality Breakthrough Concept!
Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist>
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this Browser Extension Recommendation: https://mes.fm/volume-extension
The Integral Test and Estimate of Sums
Topics to Cover
- Introduction to The Integral Test and Estimate of Sums
- The Integral Test
- Example 1
- Example 2: P-Series
- Theorem 1: P-Series
- Example 3
- Example 4
- Estimating the Sum of a Series
- Theorem 2: Remainder Estimate for the Integral Test
- Example 5
- Theorem 3
- Example 6
- Proof of the Integral Test
Introduction to The Integral Test and Estimate of Sums
In general, it is difficult to find the exact sum of a series.
We were able to accomplish this for geometric series and the series ∑1/[n(n+1)] because in each of those cases we could find a simple formula for the n-th partial sum sn.
But usually it isn't easy to compute lim n→∞ sn.
Therefore, in the next few sections, we develop several tests that enable us to determine whether a series is convergent or divergent without explicitly finding its sum.
In some cases, however, our methods will enable us to find good estimates of the sum.
Our first test involves improper integrals.
We begin by investigating the series whose terms are the reciprocals (i.e. multiplicative inverse; for example: 1/2 is a reciprocal of 2 since 1/2*2 = 1) of the squares of the positive integers:
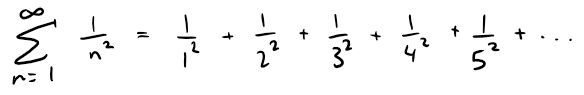
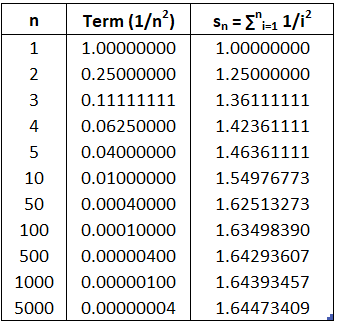
There's no simple formula for the sum sn of the first n terms, but the computer-generated table of values given below suggests that the partial sums are approaching a number near 1.64 as n→∞ and so it looks as if the series is convergent.
MES Note: The Excel file in the link below will be used throughout this document so make sure to download it and play around with it!
https://1drv.ms/x/s!As32ynv0LoaIh-wyZOENWgjV1cKeLA
Retrieved: 25 June 2019
Archive: Not Available
We can confirm this impression with a geometric argument.
The figure below shows that the curve y = 1/x2 and rectangles that lie below the curve.
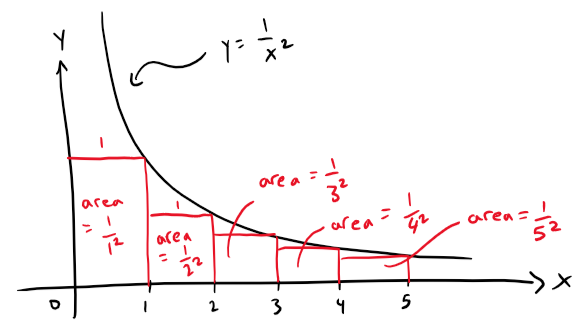
The base of each rectangle is an interval of length 1; the height is equal to the value of the function y = 1/x2 at the right endpoint of the interval.
So the sum of the areas of the rectangles is:
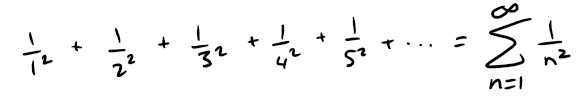
If we exclude the first rectangle (since f(x) goes to ∞ as x → 0), the total area of the remaining rectangles is smaller than the area under the curve y = 1/x2 for x ≥ 1, which is the value of the integral ∫∞1 1/x2 dx.
Recall in my earlier video on improper integrals that this improper integral is convergent and has a value 1:
https://peakd.com/mathematics/@mes/improper-integrals-type-1-infinite-intervals
Retrieved: 25 June 2019
Archive: http://archive.fo/HznuB

So the picture shows that all the partial sums (including the first rectangle) are less than:
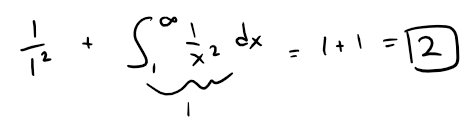
Thus the partial sums are bounded.
We also know that the partial sums are increasing (because all the terms are positive).
Therefore the partial sums converge (by the Monotonic Sequence Theorem) and so the series is convergent.
Thus the sum of the series (the limit of the partial sums) is also less than 2:
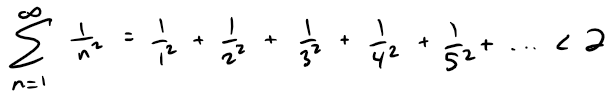
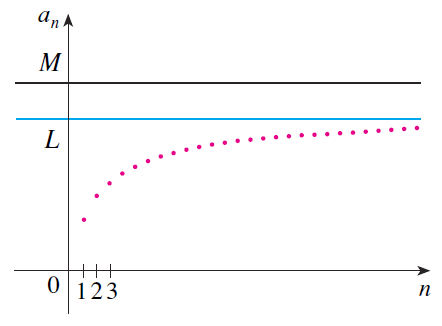
Recall the Monotonic Sequence Theorem from my earlier video on Infinite Sequences.
Retrieved: 25 June 2019
Archive: Not Available

Essentially, if a sequence is always increases (or decreasing), hence monotonic, and is bounded above (or below) then it will approach a number or limit L ≤ M (or L ≥ m if the sequence is decreasing).
Note that the exact sum of this series was found by the Swiss mathematician Leonhard Euler (1707-1783) to be π2/6, but the proof of this fact is quite difficult so I will have to prove it in a later video.
Now let's look at the series:
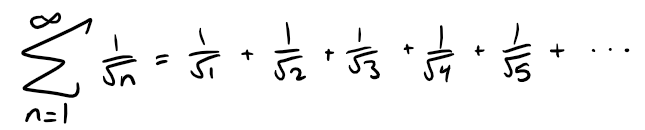
The table of values of sn suggests that the partial sums aren't approaching a finite number, so we suspect that the given series may be divergent.
Again we use a picture for confirmation.
The below figure shows the curve y = 1/x1/2, but this time we use rectangles whose tops lie above the curve.
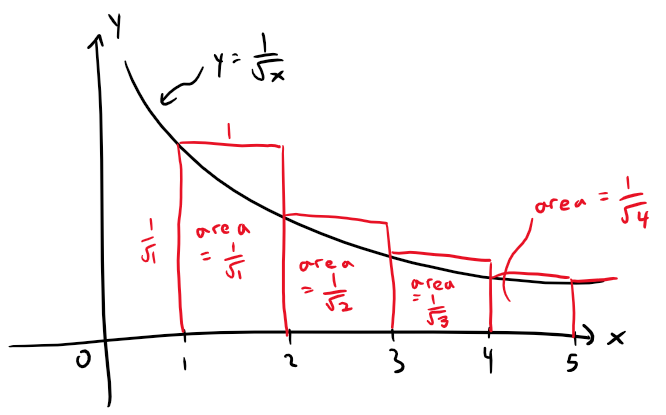
The base of each rectangle is an interval of length 1.
The height is equal to the value of the function y = 1/x1/2 at the left endpoint of the interval.
So the sum of the areas of all the rectangles is:
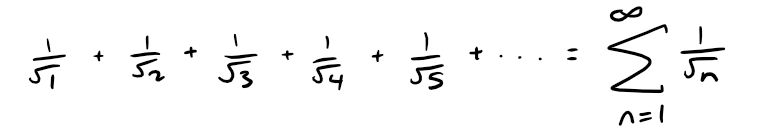
This total area is greater than the area under the curve y = 1/x1/2 for x ≥ 1, which is equal to the integral:
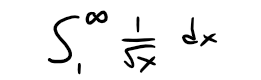
But we know from my earlier video that this improper integral is divergent.
https://peakd.com/mathematics/@mes/improper-integrals-example-4-1-x-p
Retrieved: 14 July 2019
Archive: http://archive.fo/YHnXJ

In other words, the area under the curve is infinite.
So the sum of the series must be infinite; that is, the series is divergent.
The same sort of geometric reasoning that we used for these two series can be used to prove the following test; the proof is given at the end of this section.
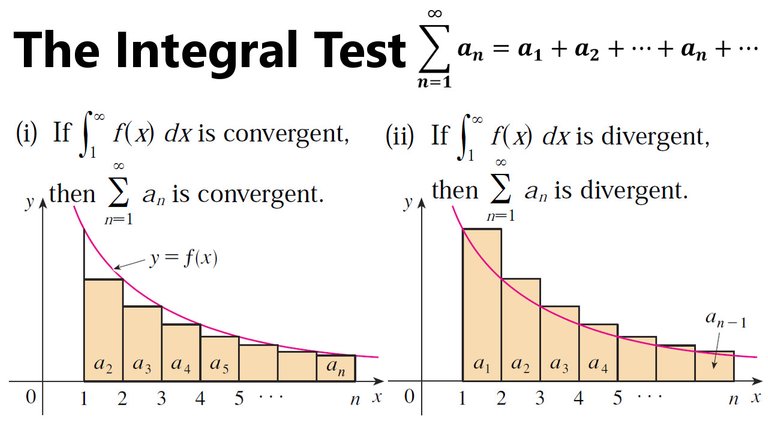
The Integral Test
Suppose f is a continuous, positive, decreasing function on [1, ∞) and let an = f(n).
Then the series ∑∞n=1 an is convergent if and only if the improper integral:
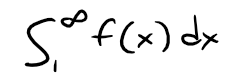
is convergent.
In other words:
(i) If ∫1∞ f(x) dx is convergent, then ∑∞n=1 an is convergent.
(ii) If ∫1∞ f(x) dx is divergent, then ∑∞n=1 an is divergent.
Note that when we use the Integral Test, it is not necessary to start the series or the integral at n = 1.
For instance, in testing the series:
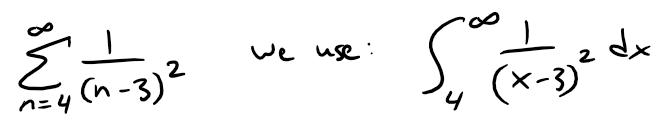
Also, it is not necessary that f be always decreasing.
What is important is that f be ultimately decreasing, that is, decreasing for x larger than some number N.
Then ∑∞n=N an is convergent, so ∑∞n=1 an is convergent by Note 4 in my previous video on Infinite Series.
Retrieved: 14 July 2019
Archive: Not Available

Example 1
Test the following series for convergence or divergence.
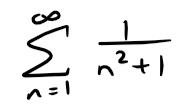
Solution:
The function f(x) = 1/(x2 + 1) is continuous, positive, and decreasing on [1, ∞) so we use the Integral Test:
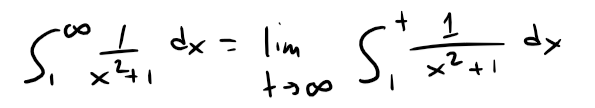
Recall that the derivative of tan-1x from my earlier video:
Retrieved: 16 July 2019
Archive: http://archive.fo/c5VBV


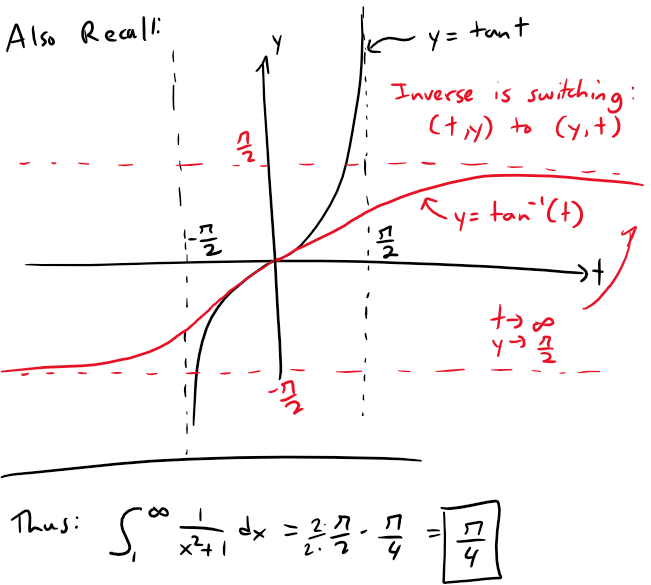
Thus ∫1∞ 1/(x2 + 1) dx is a convergent integral and so, by the Integral Test, the series ∑ 1/(n2 + 1) is convergent.
Example 2: P-Series
For what values of p is the following series convergent?
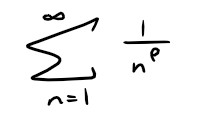
Solution:
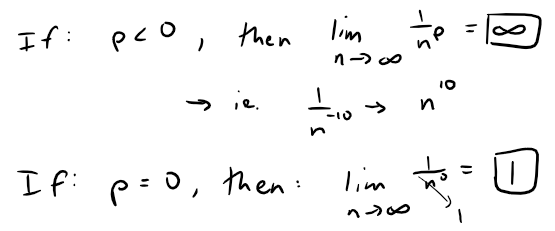
In either case, lim n→∞ (1/np) ≠ 0, so the given series diverges by the Test for Divergence also from my earlier video on Infinite Series.

If p > 0, then the function f(x) = 1/xp is clearly continuous, positive, and decreasing on [1, ∞).
Recall again from my earlier video on improper integrals which I mentioned above that:
https://peakd.com/mathematics/@mes/improper-integrals-example-4-1-x-p

It follows from the Integral Test that the series ∑ 1/np converges if p > 1 and diverges if 0 < p ≤ 1.
Note that for p = 1, this series is the Harmonic Series and which I discussed in my previous Infinite Series video as well.

Note that in order to use the Integral Test we need to be able to evaluate ∫1∞ f(x) dx and therefore we have to be able to find an antiderivative of f.
Frequently this is difficult or impossible, so we need other tests for convergence too.
The series in Example 2 is called the p-series.
It is important in the rest of this and later videos so we summarize the results of Example 2 for future reference as follows:
Theorem 1: P-Series
The p-series ∑∞n=1 1/np is convergent if p > 1 and divergent if p ≤ 1.
Example 3
(a) The series:
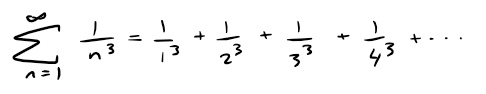
is convergent because it is a p-series with p = 3 > 1.
(b) The series:
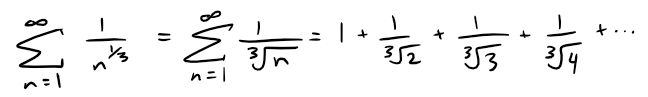
is divergent because it is a p-series with p = 1/3 < 1.
Note: We should not infer from the Integral Test that the sum of the series is equal to the value of the integral.
In fact:

Therefore, in general:
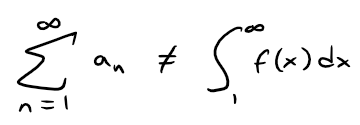
Example 4
Determine whether the following series converges or diverges:
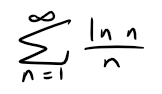
Solution:
The function f(x) = (ln x)/x is positive and continuous for x > 1 because the logarithm function is continuous.
But it is not obvious whether or not f is decreasing, so we compute its derivative:
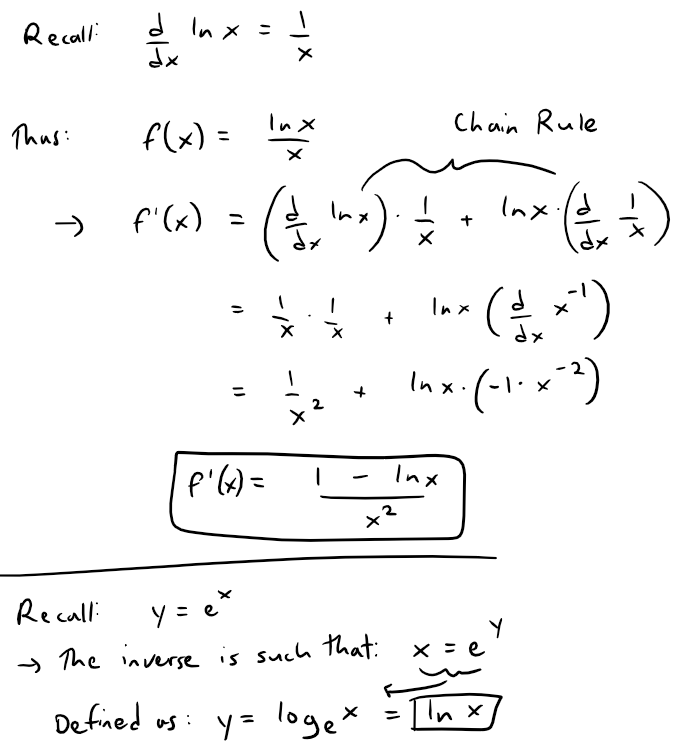
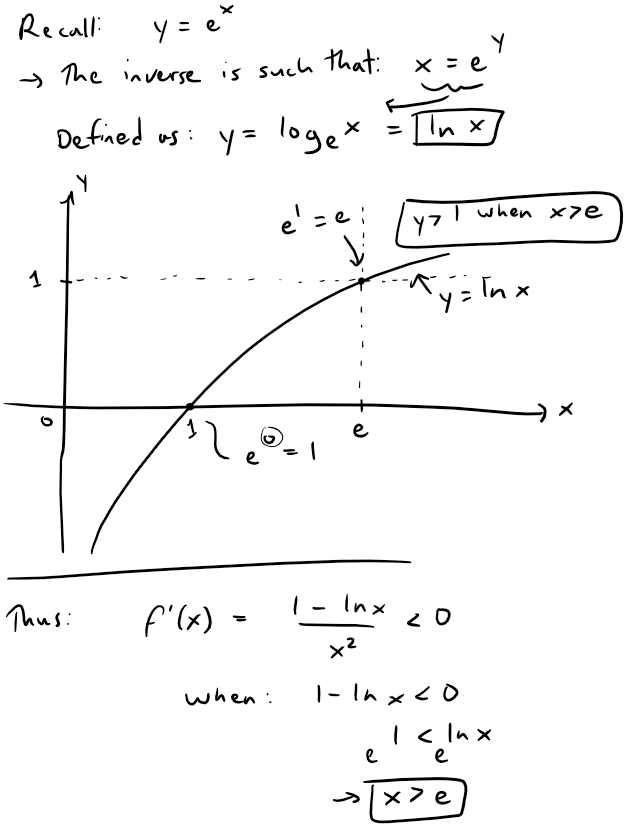
It follows that f is decreasing when x > e and so we can apply the Integral Test:
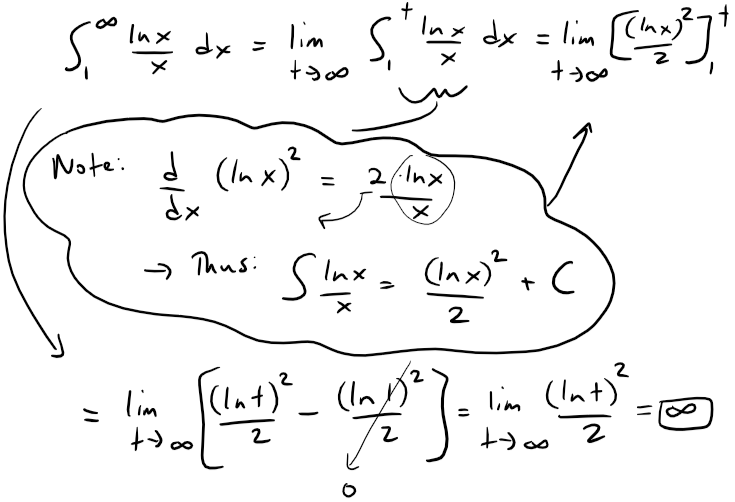
Since this improper integral is divergent, the series ∑ (ln n)/n is also divergent by the Integral Test.
Estimating the Sum of a Series
Suppose we have been able to use the Integral Test to show that a series ∑an is convergent and we now want to find an approximation to the sum s of the series.
Of course, any partial sum sn is an approximation to s because lim n→∞ sn = s.
But how good is such an approximation?
To find out, we need to estimate the size of the remainder:
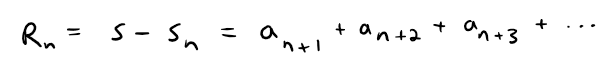
The remainder Rn is the error made when sn, the sum of the first n terms, is used as an approximation to the total sum.
We use the same notation and ideas as in the Integral Test, assuming that f is decreasing on [n, ∞).
Comparing the areas of the rectangles with the area under y = f(x) for x > n in the figure below, we see that:
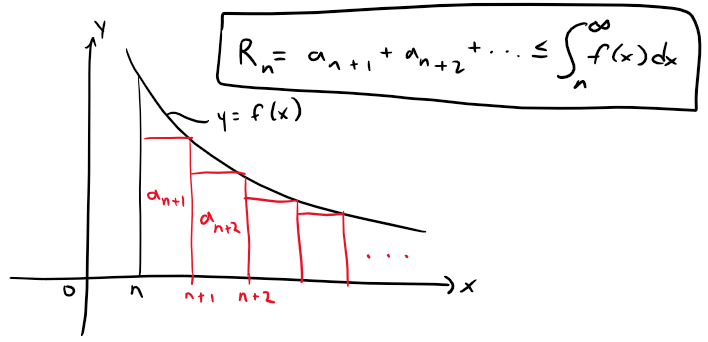
Similarly, we see from the following figure that:
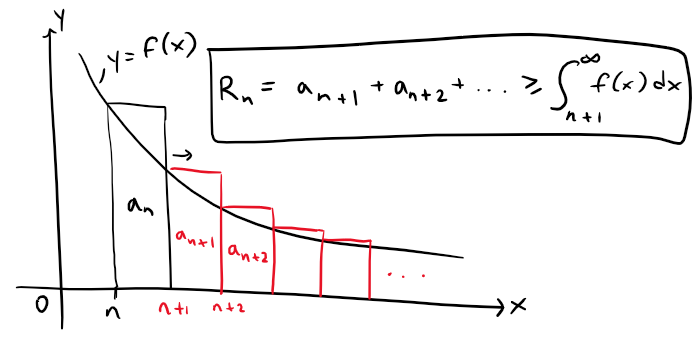
So we have proved the following error estimate:
Theorem 2: Remainder Estimate for the Integral Test
Suppose f(k) = ak , where f is a continuous, positive, decreasing function for x ≥ n and ∑ an is convergent.
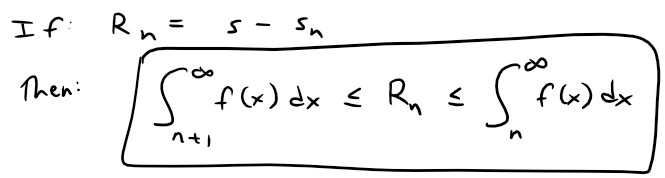
Example 5
(a) Approximate the sum of the series ∑ 1/n3 by using the sum of the first 10 terms.
Estimate the error involved in this approximation.
(b) How many terms are required to ensure that the sum is accurate to within 0.0005?
Solution:
In both parts (a) and (b) we need to know ∫n∞ f(x) dx.
With f(x) = 1/x3, which satisfies the conditions of the Integral Test, we have:
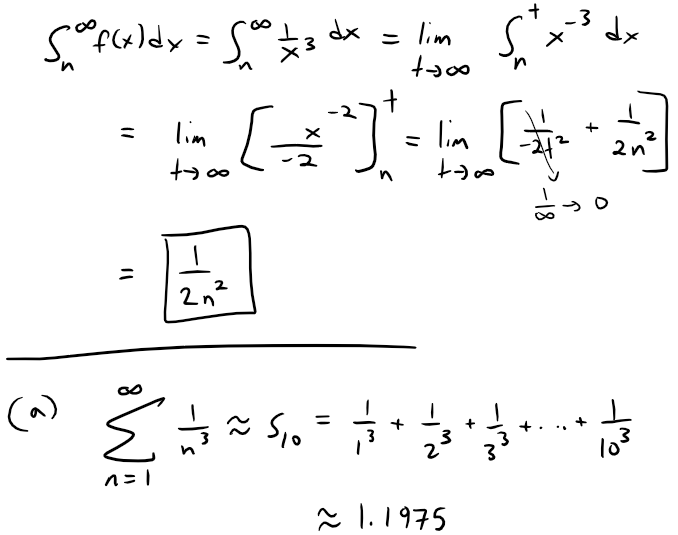
Calculation Check: s10 = 1/1^3 + 1/2^3 + 1/3^3 + 1/4^3 + 1/5^3 + 1/6^3 + 1/7^3 + 1/8^3 + 1/9^3 + 1/10^3 = 1.1975.
According to the remainder estimate in Theorem 2, we have:
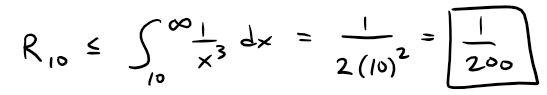
So the size of the error is at most 1/200 = 0.005.
(b) Accuracy to within 0.0005 means that we have to find a value of n such that Rn ≤ 0.0005.
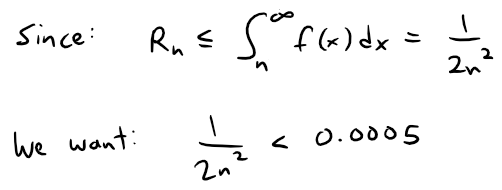
Solving this inequality, we get:
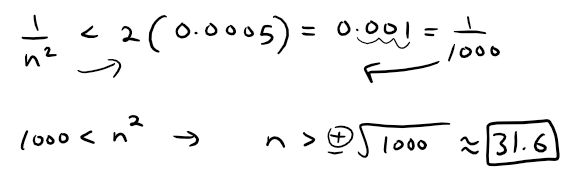
Calculation Check: 1000^(1/2) = 31.6228.
We need 32 terms to ensure accuracy to within 0.0005.
Theorem 3
If we add sn to each side of the inequalities in Theorem 2, we get:
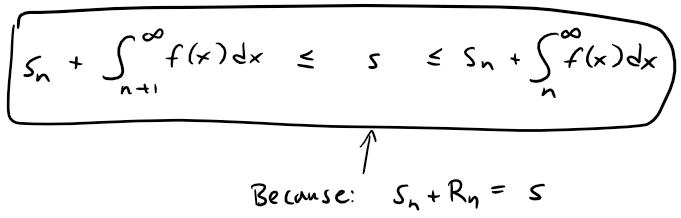
The inequalities in Theorem 3 give a lower bound and an upper bound for s.
They provide a more accurate approximation to the sum of the series than the partial sum sn does.
Example 6:
Use Theorem 3 with n = 10 to estimate the sum of the following series:
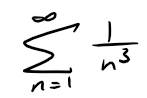
Solution:
The inequalities in Theorem 3 become:
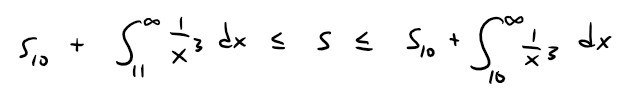
From Example 5 we know that:
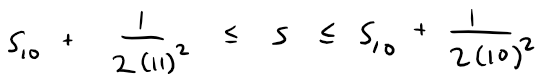
Using s10 ≈ 1.197532 (note the extra 32 is just a more fine tuned calculation my calculus book uses which my OneNote automatic calculator cuts off), we get:
1.201664 ≤ s ≤ 1.202532
Calculation Check:
- 1.197532 + 1/(2*11^2) = 1.201664
- 1.197532 + 1/(2*10^2) = 1.202532
If we approximate s by the midpoint of this interval, then the error is at most half the length of the interval.
The interval length is: 1.202532 - 1.201664 = 0.000868.
The midpoint or average value is (1.201664+1.202532)/2 = 1.202098 ≈ 1.2021.
Thus, the max error is half the interval length: 0.000868/2 = 0.000434 < 0.0005.
So:
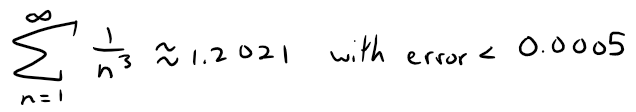
If we compare Example 6 with Example 5, we see that the improved estimate in Theorem 3 can be much better than the estimate s ≈ sn.
To make the error smaller than 0.0005 we had to use 32 terms in Example 5 but only 10 terms in Example 6.
Proof of the Integral Test
We have already seen the basic idea behind the proof of the Integral Test in earlier figures for the series ∑ 1/n2 and ∑ 1/n1/2.
For a general series ∑ an, look at the following figures.
The area of the first rectangle in Figure 1 is the value of f at the right endpoint of [1, 2], that is, f(2) = a2.
So, comparing the areas of the rectangles with the area under y = f(x) from 1 to n, we see that:
Figure 1: Rectangles below f(x)
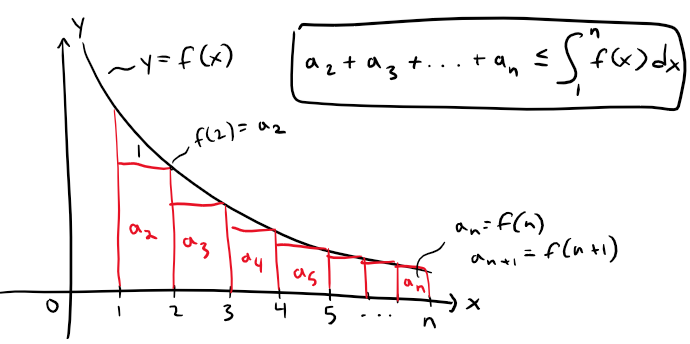
Notice that this inequality depends on the fact that f is decreasing.
Likewise Figure 2 shows that:
Figure 2: Rectangles above f(x)
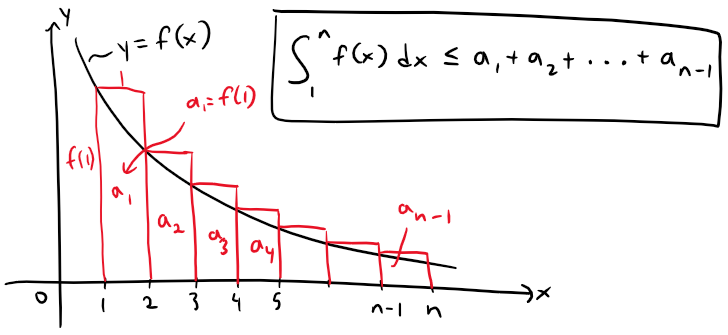
Thus we have two scenarios:
(i) If ∫1∞ f(x) dx is convergent, then Figure 1 gives:
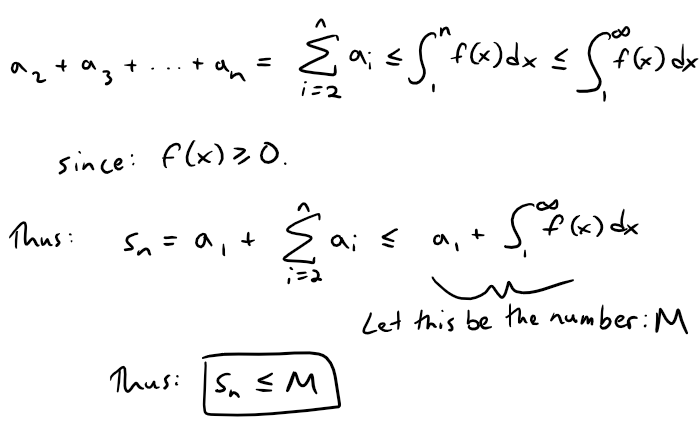
Since sn ≤ M for all n, the sequence {sn} is bounded above.
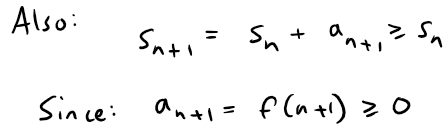
Thus {sn} is an increasing bounded sequence and so it is convergent by the Monotonic Sequence Theorem, mentioned earlier above from my Infinite Sequences video.
This means that ∑ an is convergent.
(ii) If ∫1∞ f(x) dx is divergent, then ∫1n f(x) dx → ∞ as n→∞ because f(x) ≥ 0.
But Figure 2 gives:

This implies that sn → ∞ and so ∑ an diverges.
Thanks for the post! I didn't have time for the whole video, but I read through the notes, and listened to part of the video while I was doing it. It is useful information for anyone with an interest in learning more about mathematics.
I included a link to your article in my recent post, Science and technology micro-summaries for July 20, 2019, and set a beneficiary reward so that you'll receive 5% of the rewards.
Sweet thanks for sharing my post and sharing some of the rewards! :)