Quadratic Formula by Completing the Square
In this video I solve the quadratic equation by completing the square to obtain the famous quadratic formula. I had done a similar video 13 years ago so I thought it was time to do an updated one. Completing the square involves working backwards from the quadratic equation to obtain a form that has a square, that is of the form (x + d)2. From here we can take the square root and rearrange to solve for x, which obtains 2 values because of the nature of the square root.
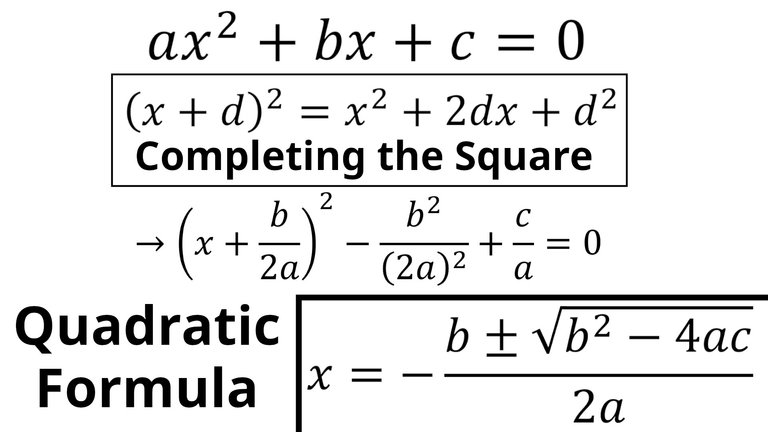
Time stamps
- Recap on Quadratic Formula: 0:00
- Derivation by completing the square: 0:30
- Completing the square: 1:16
- Quadratic equation as a square: 2:46
- Obtaining a common denominator: 4:25
- Quadratic formula: 5:58
Notes and playlists
- Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EF05ExjzLbB64NgUjoV1hl
- Notes: https://peakd.com/hive-128780/@mes/dzekfnxh
- PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIjYlhWw4dLq59fn0Xwg .
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: [email protected]
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
▶️ 3Speak
!summarize
Part 1/5:
Understanding the Quadratic Formula
In the world of algebra, few equations are as pivotal as the quadratic equation. It takes the form of ( ax^2 + bx + c = 0 ), where ( a ), ( b ), and ( c ) are constants, and ( x ) represents the unknown variable we want to solve for.
The overarching goal is to determine the values of ( x ) that satisfy this equation. By using the quadratic formula, the roots (or solutions) of the quadratic equation can be succinctly expressed as:
[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
This formula is derived through a method known as completing the square.
Revisiting the Derivation
Part 2/5:
The speaker begins by acknowledging their previous work on this topic, which dates back over a decade. With a desire for clarity and completeness in understanding the quadratic formula, a fresh derivation is proposed, aligning with the principles of completing the square.
To start, they restate the quadratic equation:
[
ax^2 + bx + c = 0
]
Next, to simplify, the equation is divided by ( a ), eliminating the leading coefficient:
[
x^2 + \frac{b}{a}x + \frac{c}{a} = 0
]
Now, the structure is amenable to completing the square. The plan is to express the quadratic in a form that allows for easier manipulation.
Completing the Square
The speaker suggests defining a new term ( d ), where ( 2d = \frac{b}{a} ). Solving for ( d ) yields:
[
d = \frac{b}{2a}
]
Part 3/5:
Using ( d ), the equation can be rewritten, leading to the expression ( (x + d)^2 ). Expanding this square reveals:
[
(x + d)^2 = x^2 + 2dx + d^2
]
This transformation is significant as it allows for the consolidation of terms, providing a path towards expressing everything in one elegant equation.
After some manipulation, the aim is to rearrange the equation. The speaker guides the audience through moving some terms around, leading to a more manageable equation:
[
(x + \frac{b}{2a})^2 = \frac{b^2}{4a^2} - \frac{c}{a}
]
Further simplification and togetherness of fractions result in:
[
(x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2}
]
Now at a critical point, squaring both sides leads us towards the solutions for ( x ).
Solve for ( x )
Part 4/5:
Taking the square root on both sides gives:
[
x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a}
]
Rearranging this equation to isolate ( x ) finally leads to the final derivation of the quadratic formula:
[
x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a}
]
This can be combined into a single fraction, revealing the complete quadratic formula once more:
[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
Conclusion
The speaker successfully derives the quadratic formula anew, reinforcing the value of understanding mathematical concepts through different methodologies. By revisiting the completing the square method, they demonstrate how foundational techniques in algebra continue to hold relevance and clarity for learners today.
Part 5/5:
With this fresh perspective, the quadratic formula remains an essential tool in tackling various equations across different fields of study, unlocking the mysteries of parabolic relationships inherent in mathematics.