Vectors and the Geometry of Space: Cylinders and Quadric Surfaces
▶️Watch on 3Speak - Odysee - BitChute - Rumble - DTube - YouTube - PDF notes
In this video I explore the wonderful world of cylinders and quadric surfaces. Cylinders are defined as a 3D surface that consists of all lines (called rulings) that are parallel to a given line and pass through a given plane curve. Quadric surfaces are the graphs of a second-degree equation in three variables x, y, and z. Unlike quadric surfaces, cylinders have 1 of the x, y, or z variables missing from its equation. This makes the cylinder extend outwards along the missing variable. I also go over some exercises and show that the Earth can be more accurately modeled as an ellipsoid, which is a type of quadric surface. This section is part of the Vectors and Geometry of Space chapter in my Calculus book.
The topics covered as well as their timestamps are listed below.
- Intro: 0:00
- Calculus Book Reference: 0:50
- Sections in Calculus Book Chapter: 1:03
- Topics to Cover: 1:49
- Cylinders and Quadric Surfaces: 3:22
- Cylinders: 5:10
- Example 1: Parabolic Cylinder: 5:28
- Example 2: Circular Cylinders: 10:31
- (a) Vertical Cylinder: 10:44
- (b) Horizontal Cylinder: 14:45
- Note: 3D Surfaces vs 2D Traces: 17:40
- Quadric Surfaces: 18:54
- Example 3: Ellipsoid: 24:23
- Example 4: Elliptic Paraboloid: 37:25
- Example 5: Hyperbolic Paraboloid: 45:01
- Example 6: Hyperboloid of One Sheet: 1:06:03
- Computer-Drawn Graphs of Quadric Surfaces: 1:12:19
- Table 1: Graphs of Quadric Surfaces: 1:12:57
- Example 7: Hyperboloid of Two Sheets: 1:18:13
- Example 8: Elliptic Paraboloid: 1:29:36
- Applications of Quadric Surfaces: 1:41:25
- Exercises
- Exercise 1: Modeling Earth as an Ellipsoid: 1:46:54
- (a) Earth's Ellipsoid Equation: 1:48:06
- (b) Parallels or Circular Lines of Equal Latitude: 1:53:24
- (c) Meridians or Elliptical Lines of Equal Longitude: 1:58:56
- Exercise 2: Hyperbolic Paraboloid Generated from Lines: 2:05:51
- Exercise 1: Modeling Earth as an Ellipsoid: 1:46:54
- Outro: 2:21:43
Playlists
Video sections - Vectors and the Geometry of Space
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Vectors and the Geometry of Space: Cylinders and Quadric Surfaces
Calculus Book Reference
Note that I mainly follow along the following calculus book:
- Calculus: Early Transcendentals 7th Edition by James Stewart
- Note: In the earlier videos I used the 6th edition.
Sections in Calculus Book Chapter
I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.
Note that I have started splitting each long video into sections and made a playlist for each.
- 3-D Coordinate Systems
- Vectors
- The Dot Product - Playlist
- The Cross Product - Playlist
- Equations of Lines and Planes - Playlist
- Cylinders and Quadric Surfaces - playlist - Current Video
- Review
- True-False Quiz
- Problems Plus
Topics to Cover
Note that the timestamps will be included in the video description for each topic listed below.
- Cylinders and Quadric Surfaces
- Cylinders
- Example 1: Parabolic Cylinder
- Example 2: Circular Cylinders
- (a) Vertical Cylinder
- (b) Horizontal Cylinder
- Note: 3D Surfaces vs 2D Traces
- Quadric Surfaces
- Example 3: Ellipsoid
- Example 4: Elliptic Paraboloid
- Example 5: Hyperbolic Paraboloid
- Example 6: Hyperboloid of One Sheet
- Computer-Drawn Graphs of Quadric Surfaces
- Table 1: Graphs of Quadric Surfaces
- Example 7: Hyperboloid of Two Sheets
- Example 8: Elliptic Paraboloid
- Applications of Quadric Surfaces
- Exercises
- Exercise 1: Modeling Earth as an Ellipsoid
- (a) Earth's Ellipsoid Equation
- (b) Parallels or Circular Lines of Equal Latitude
- (c) Meridians or Elliptical Lines of Equal Longitude
- Exercise 2: Hyperbolic Paraboloid Generated from Lines
- Exercise 1: Modeling Earth as an Ellipsoid
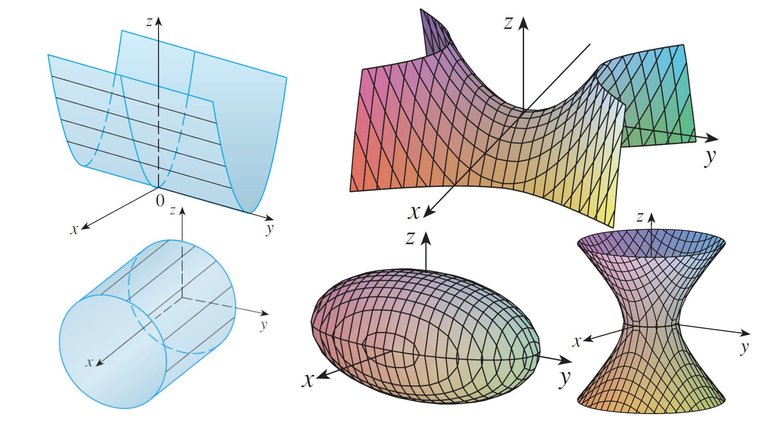
Cylinders and Quadric Surfaces
We have already looked at two special types of surfaces: planes and spheres.
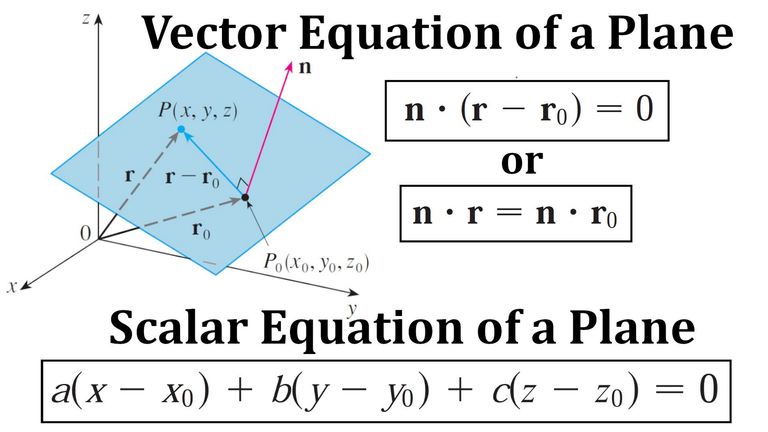

Here we investigate two other types of surfaces: cylinders and quadric surfaces.
In order to sketch the graph of a surface it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes.
These curves are called traces (or cross-sections) of the surface.
Cylinders
A cylinder is a surface that consists of all lines (called rulings) that are parallel to a given line and pass through a given plane curve.
Example 1: Parabolic Cylinder
Sketch the graph of the surface z = x2.
Solution:
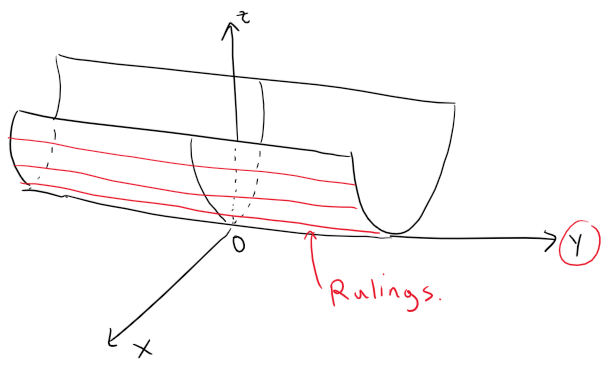
Notice that the equation of the graph, z = x2, doesn't involve y.
This means that any vertical plane with equation y = k (parallel to the xz-plane) intersects the graph in a curve with equation z = x2.
So these vertical traces are parabolas.
The figure below shows how the graph is formed by taking the parabola z = x2 in the xz-plane and moving it in the direction of the y-axis.
Here is the graph in GeoGebra's 3D graphing calculator: https://www.geogebra.org/3d/tabys4ec
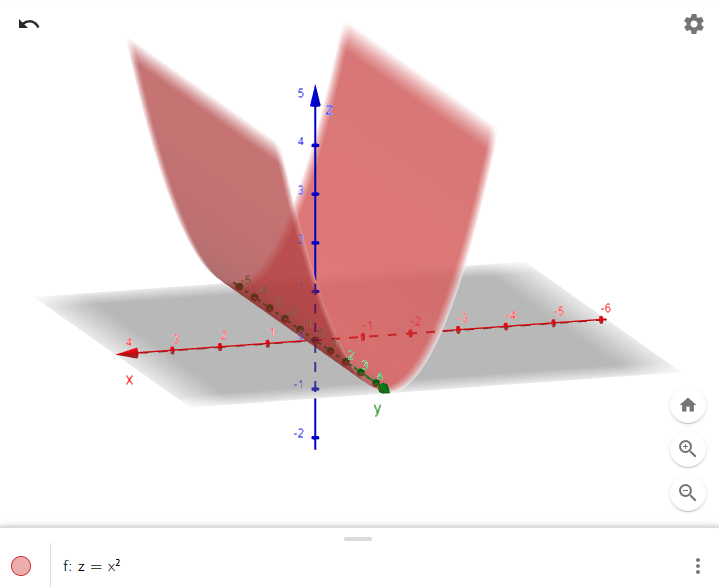
The graph is a surface, called a parabolic cylinder, made up of infinitely shifted copies of the same parabola.
Here the rulings of the cylinder are parallel to the y-axis.
We noticed that the variable y is missing from the equation of the cylinder in Example 1.
This is typical of a surface whose rulings are parallel to one of the coordinate axes.
If one of the variables x, y, or z is missing from the equation of a surface, then the surface is a cylinder.
Example 2: Circular Cylinders
Identify and sketch the surfaces:
(a) x2 + y2 = 1
(b) y2 + z2 = 1
Solution to (a): Vertical Cylinder
Since z is missing and the equations x2 + y2 = 1, z = k represent a circle with radius 1 in the plane z = k, the surface x2 + y2 = 1 is a circular cylinder whose axis is the z-axis.
Here the rulings are vertical lines.
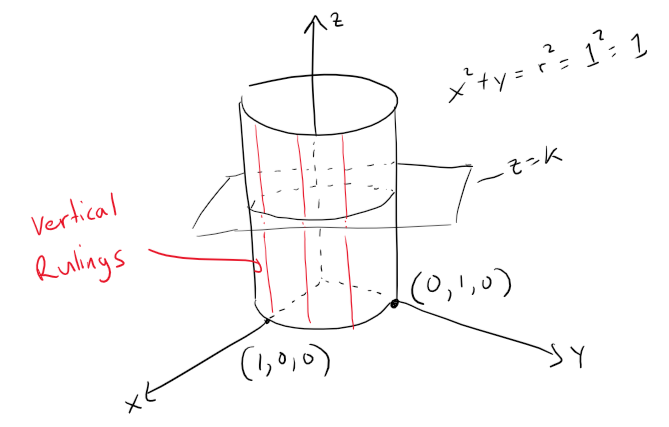
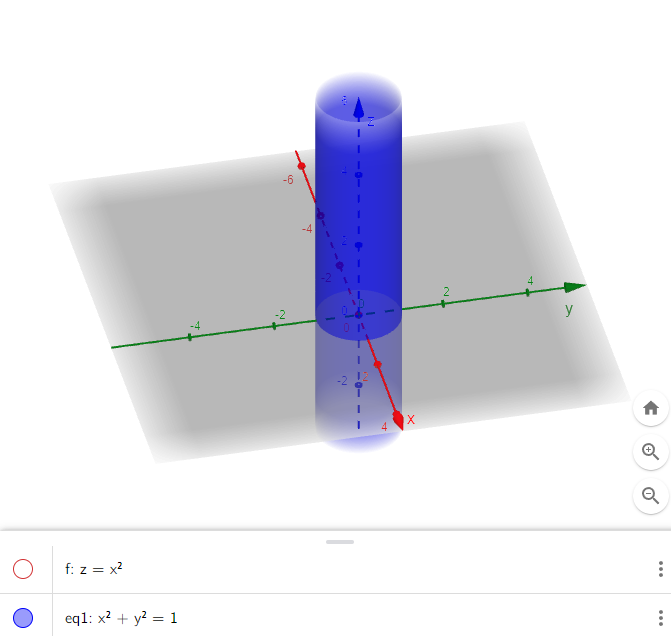
Graphing in GeoGebra.
https://www.geogebra.org/3d/tabys4ec
Solution to (b): Horizontal Cylinder
In this case x is missing and the surface is a circular cylinder whose axis is the x-axis.
It is obtained by taking the circle y2 + z2 = 1, x = 0 in the yz-plane and moving it parallel to the x-axis.
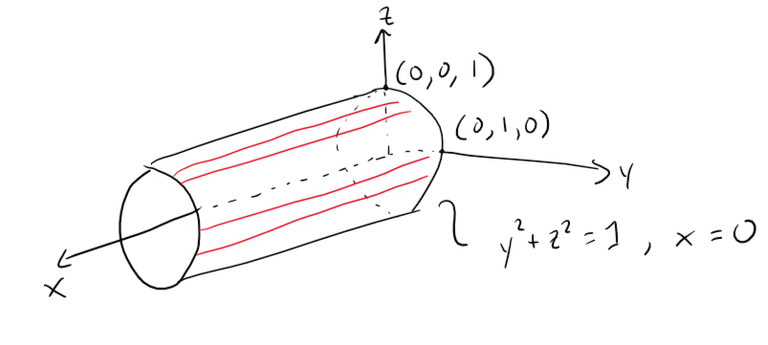
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec

Note: 3D Surfaces vs 2D Traces
When you are dealing with surfaces, it is important to recognize that an equation like x2 + y2 = 1 represents a cylinder and not a circle.
The trace of a cylinder x2 + y2 = 1 in the xy-plane is the circle with equations x2 + y2 = 1, z = 0.
Quadric Surfaces
A quadric surface is the graph of a second-degree equation in three variables x, y, and z.
The most general such equation is:
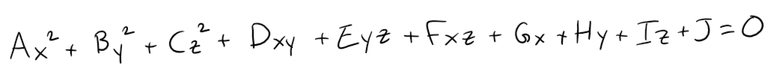
where A, B, C, … , J are constants, but by translation and rotation (and completing the square) it can be brought into one of the two standard forms:
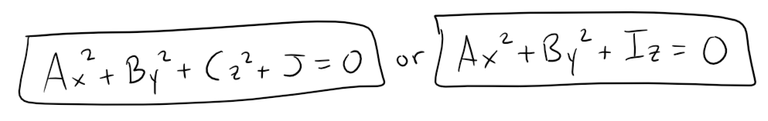
Quadric surfaces are the counterparts in three dimensions of the conic sections in the plane.
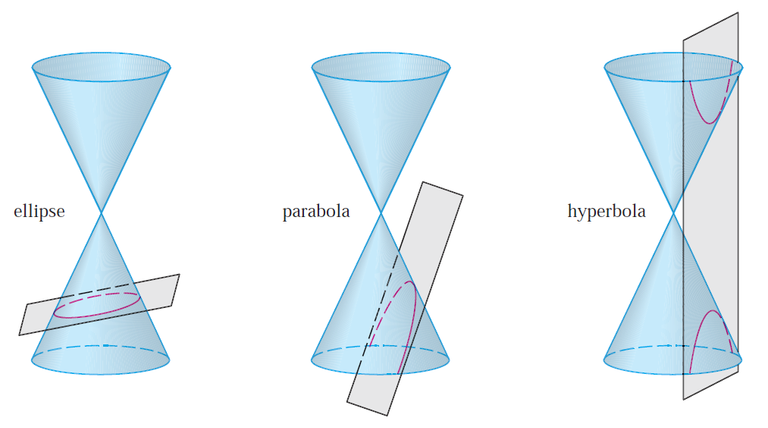
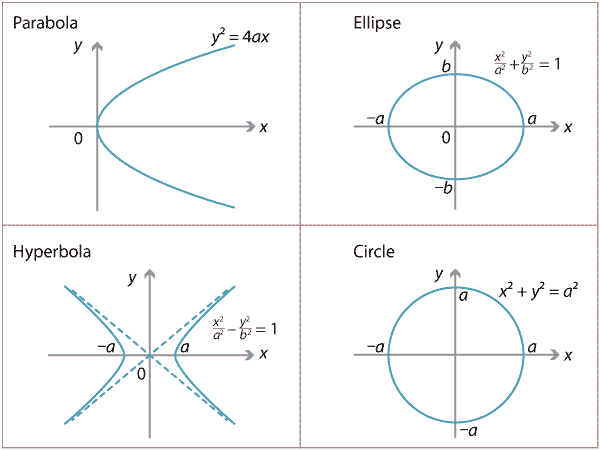
Image: Equations of conic sections
Example 3: Ellipsoid
Use traces to sketch the quadric surface with equation:
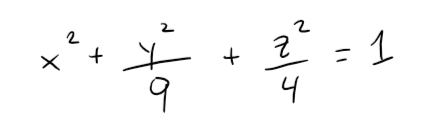
Solution:
By substituting z = 0, we find the trace in the xy-plane is:
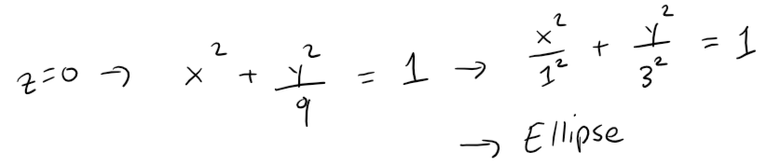
which we recognize as an equation of an ellipse.
In general, the horizontal trace in the plane z = k is:
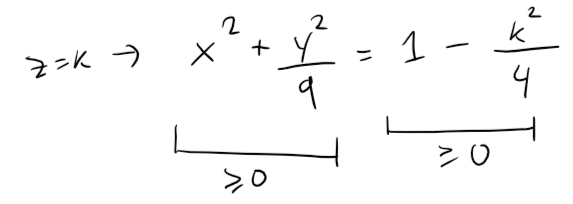
which is an ellipse, provided that k2 < 4, that is, - 2 < k < 2. This is so that the right side isn't negative (or zero) since the left side is always positive.
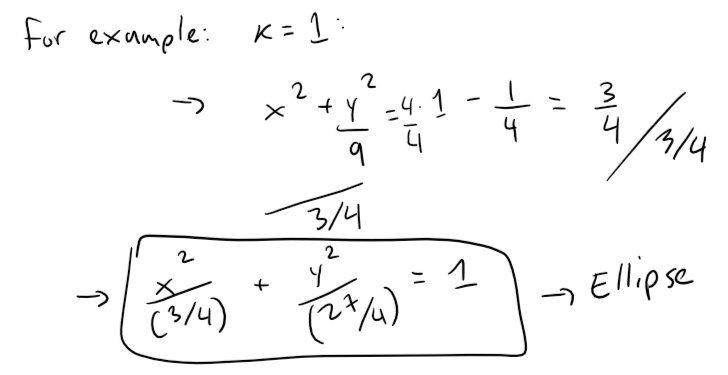
Similarly, the vertical traces are also ellipses:
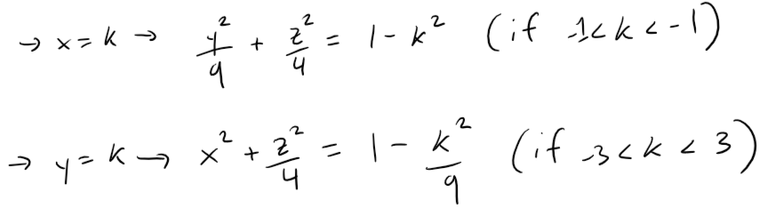
The figure below shows how drawing some traces indicates the shape of the surface.
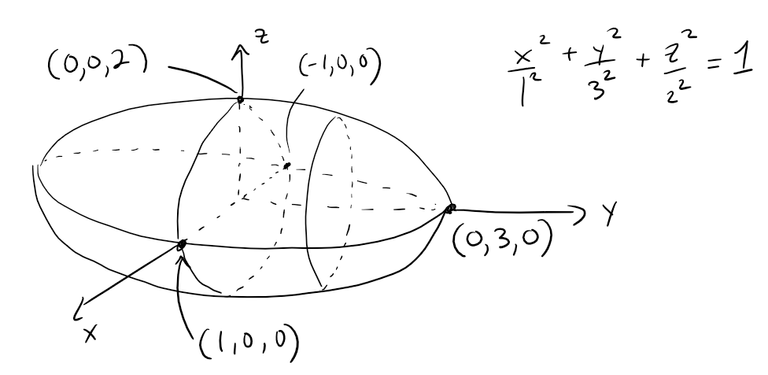
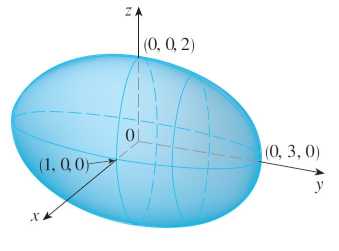
Here is a better image from my Calculus book.
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
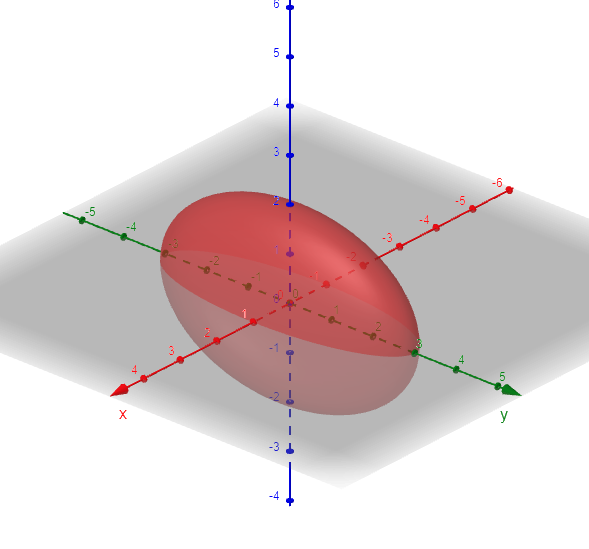
It's called an ellipsoid because all of its traces are ellipses.
Notice that it is symmetric with respect to each coordinate plane; this is a reflection of the fact that its equation involves only even powers of x, y, and z.
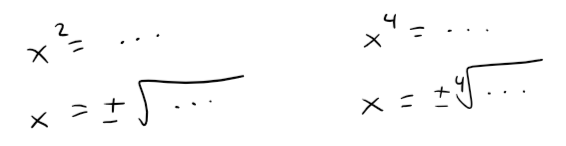
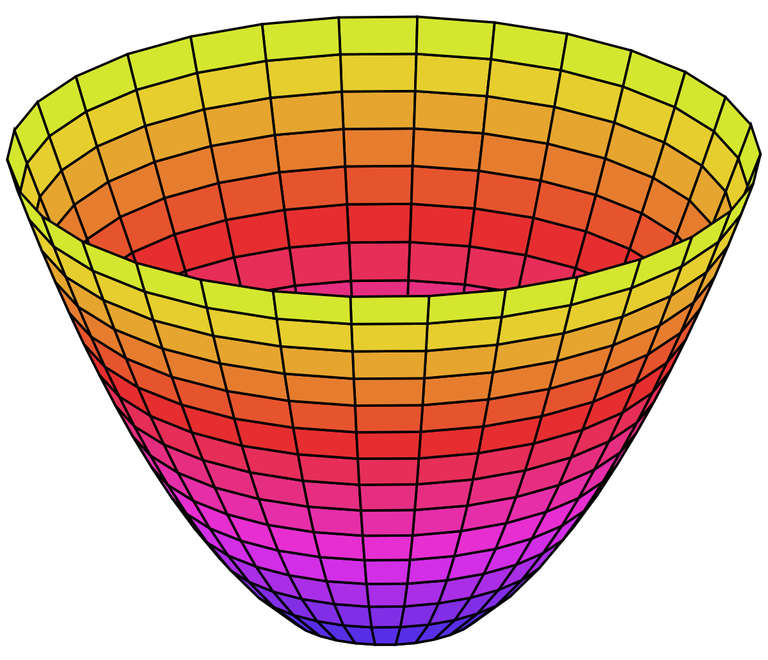
Example 4: Elliptic Paraboloid
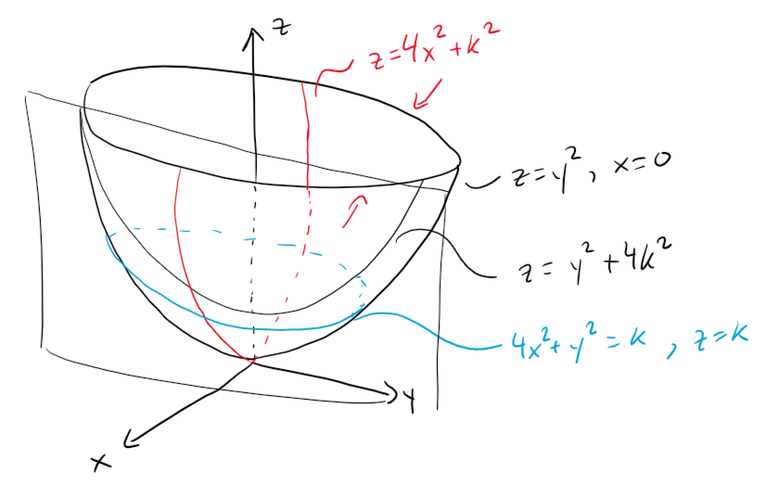
Use traces to sketch the surface z = 4x2 + y2.
Solution:
If we put x = 0, we get z = y2, so the yz-plane intersects the surface in a parabola.
If we put x = k (a constant), we get z = y2 + 4k2.
This means that if we slice the graph with any plane parallel to the yz-plane, we obtain a parabola that opens upward.
Similarly, if y = k, the trace is z = 4x2 + k2, which is again a parabola that opens upwards.
If we put z = k, we get the horizontal traces 4x2 + y2 = k, which we recognize as a family of ellipses.
Knowing the shapes of the traces, we can sketch the graph below.
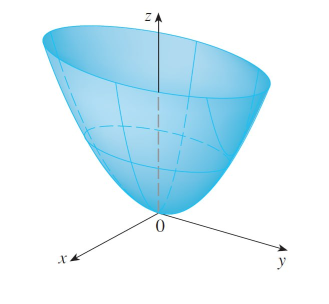
Here is a more clear image from my Calculus book.
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
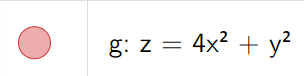
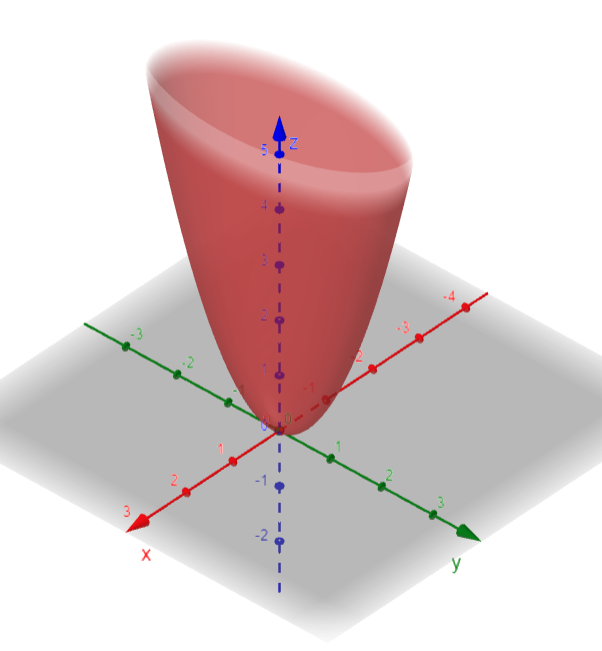
Because of the elliptical and parabolic traces, the quadric surface z = 4x2 + y2 is called an elliptic paraboloid.
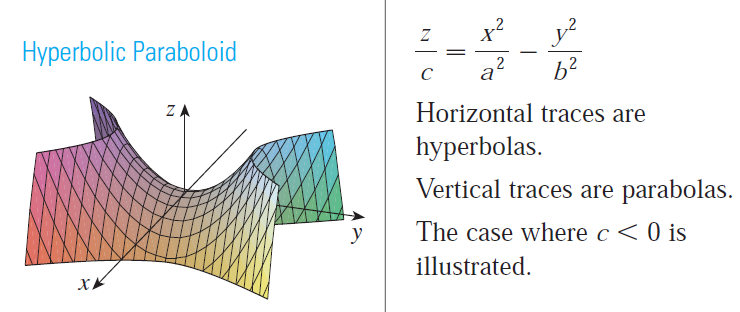
Example 5: Hyperbolic Paraboloid
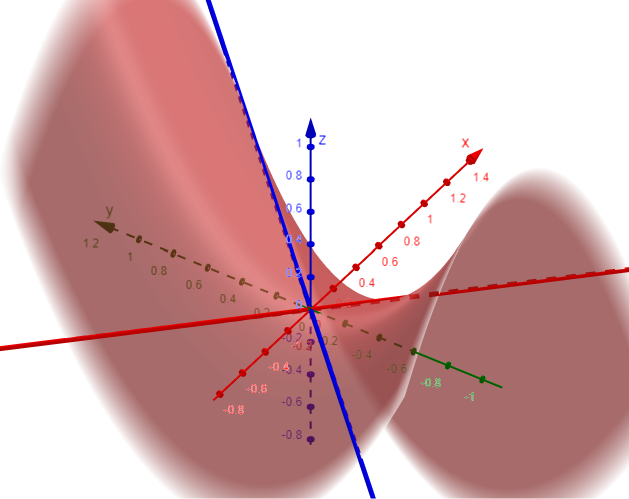
Sketch the surface z = y2 - x2.
Solution:
The traces in the vertical planes x = k are the parabolas z = y2 - k2, which open upward.
The traces in y = k are the parabolas z = -x2 + k2, which open downward.
The horizontal traces are y2 - x2 = k, a family of hyperbolas.
We can draw the family of traces below and show how the traces appear when placed in their correct planes.
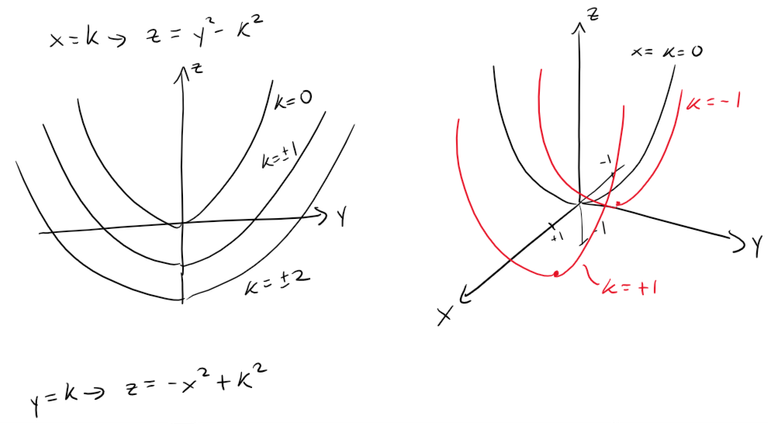
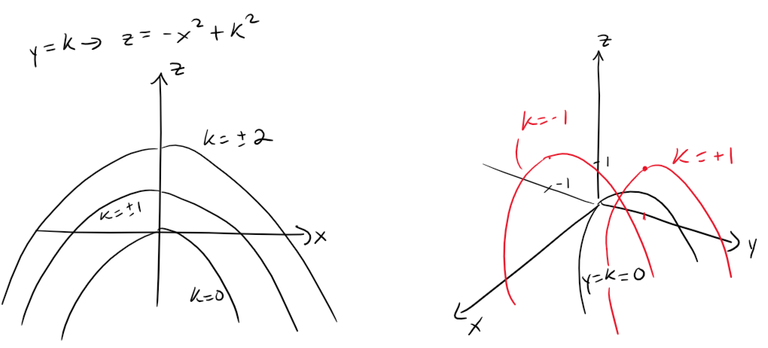
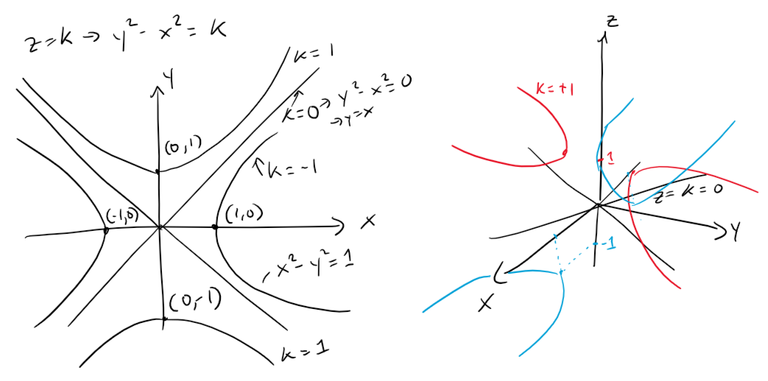
For clarity, here are the graphs from my calculus book.
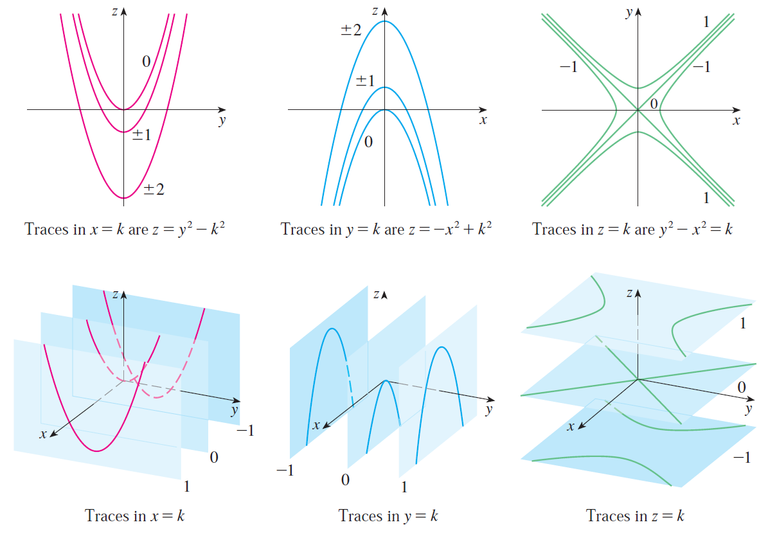
If we fit together the traces, we can form the surface z = y2 - x2, a hyperbolic paraboloid.
For clarity, here is the graph from my calculus book.

Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec

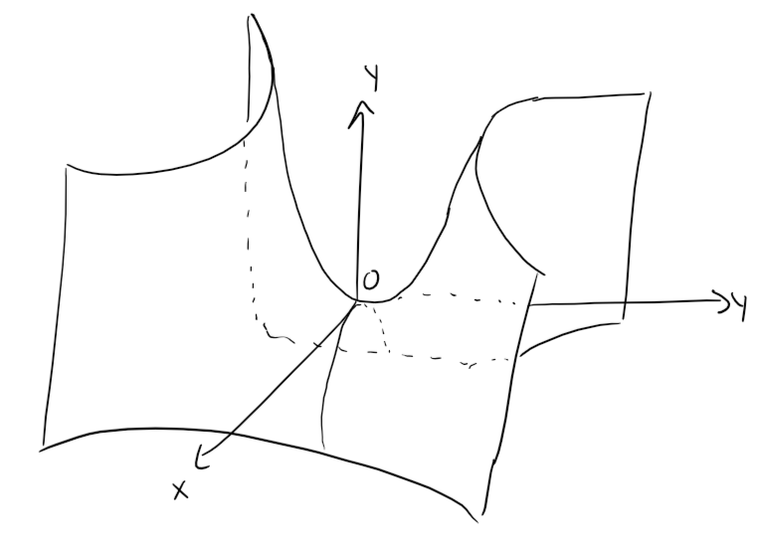
Notice that the shape of the surface near the origin resembles that of a saddle.
This surface will be investigated further in a future video when we discuss saddle points.
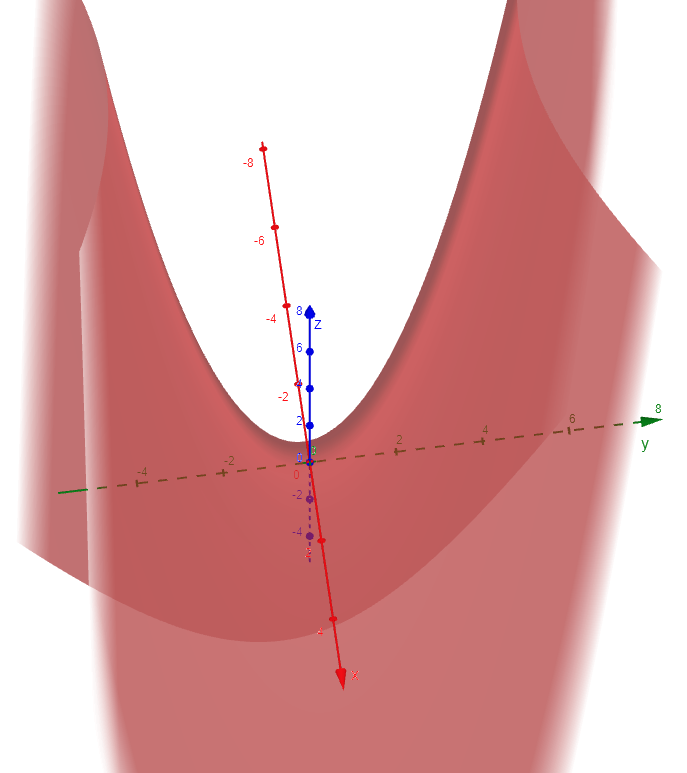
Example 6: Hyperboloid of One Sheet
Sketch the surface:
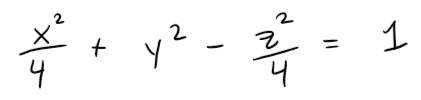
Solution:
The trace in any horizontal plane z = k is the ellipse:
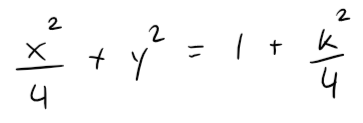
but the traces in the xz and yz-planes are the hyperbolas:
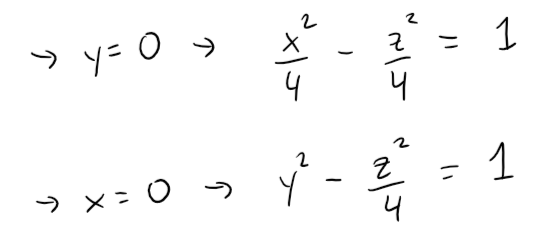
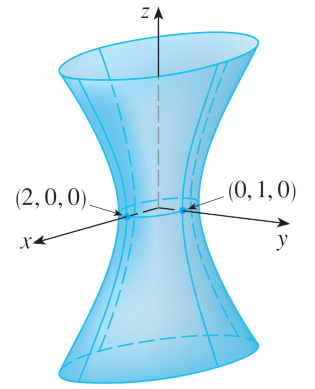
This surface is called a hyperboloid of one sheet and is sketched below.

Here is the same image from my Calculus book:
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
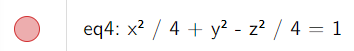
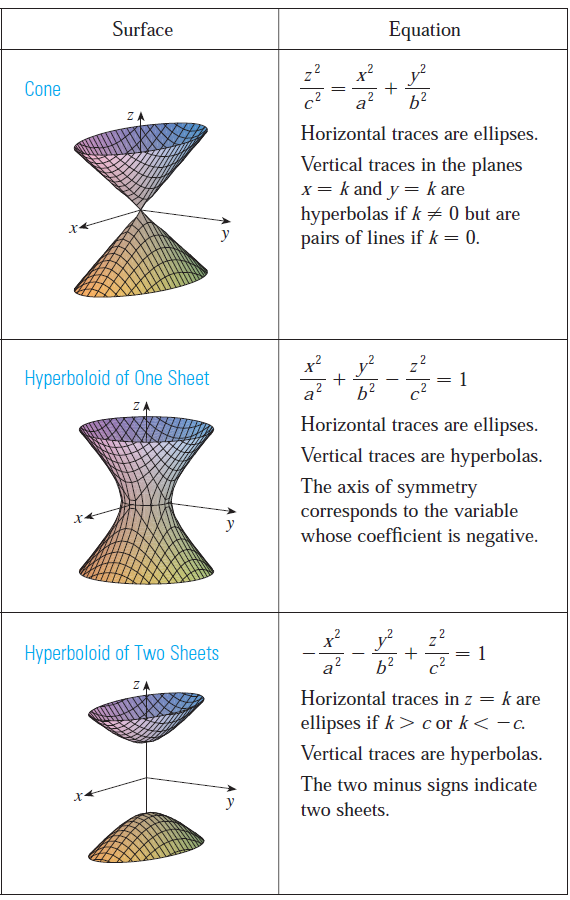
Computer-Drawn Graphs of Quadric Surfaces
The idea of using traces to draw a surface is employed in three-dimensional graphing software for computers.
In most such software, traces in the vertical planes x = k and y = k are drawn for equally spaced values of k, and parts of the graph are eliminated using hidden line removal.
Table 1 shows computer drawn graphs of the six basic types of quadric surfaces in standard form.
All surfaces are symmetric with respect to the z-axis.
If a quadric surface is symmetric about a different axis, its equation changes accordingly.
Table 1: Graphs of quadric surfaces

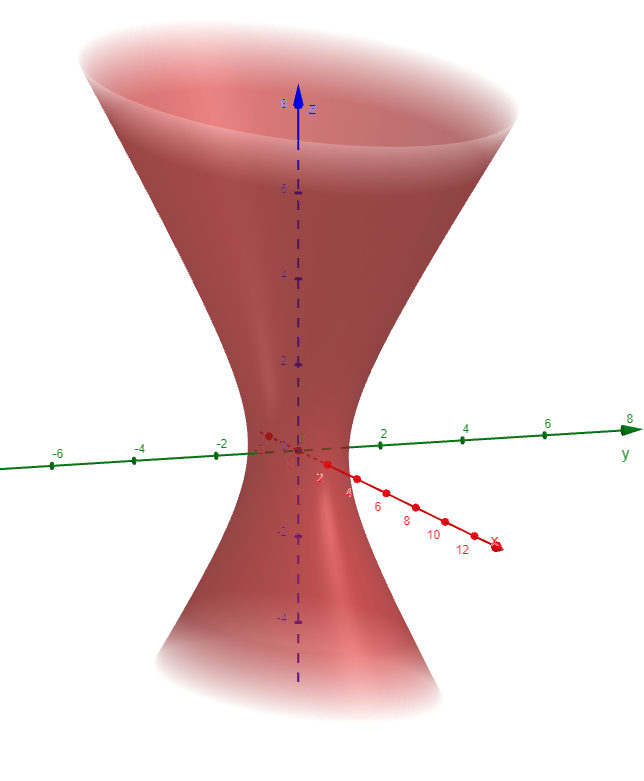
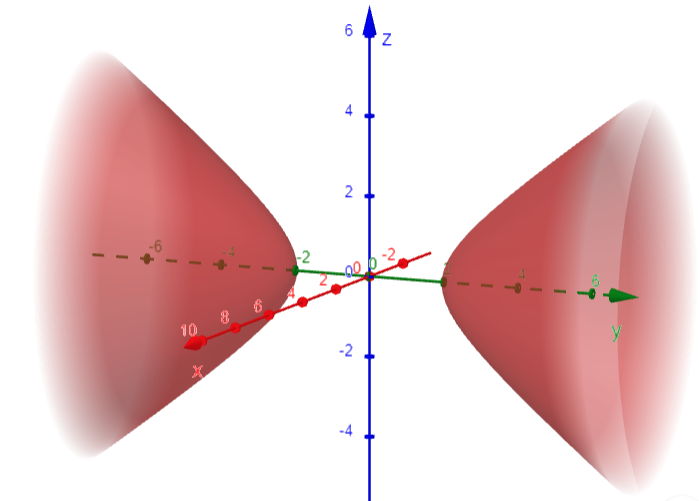
Example 7: Hyperboloid of Two Sheets
Identify and sketch the surface 4x2 - y2 + 2z2 + 4 = 0.
Solution:
Dividing by -4, we first put the equation in standard form:
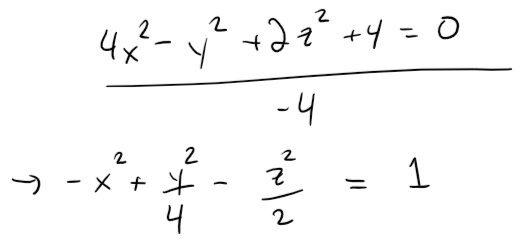
Comparing this equation with Table 1, we see it represents a hyperboloid of two sheets, the only difference being that in this case the axis of the hyperboloid is the y-axis.
The traces in the xy and yz-planes are the hyperbolas:
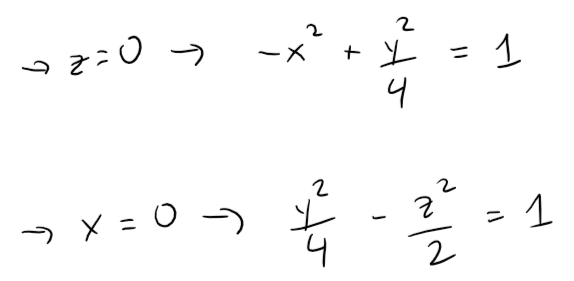
The surface has no trace in the xz-plane, but traces in the vertical planes y = k for |k| > 2 are the ellipses:
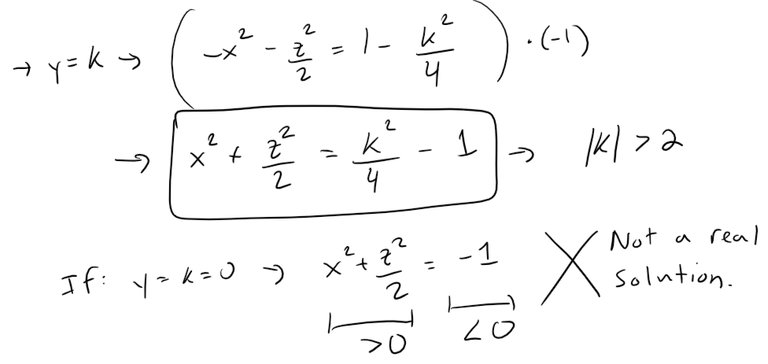
The above equation can be written as:

These traces are used to make the sketch below.

Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec

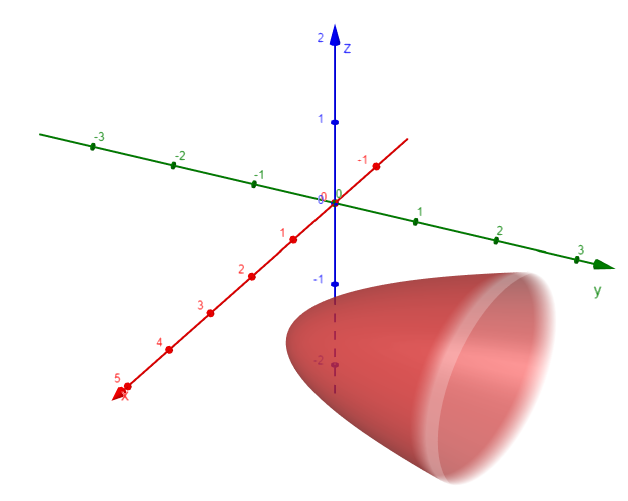
Example 8: Elliptic Paraboloid
Classify the quadric surface x2 + 2z2 - 6x - y + 10 = 0.
Solution:
By completing the square we can rewrite the equation as:
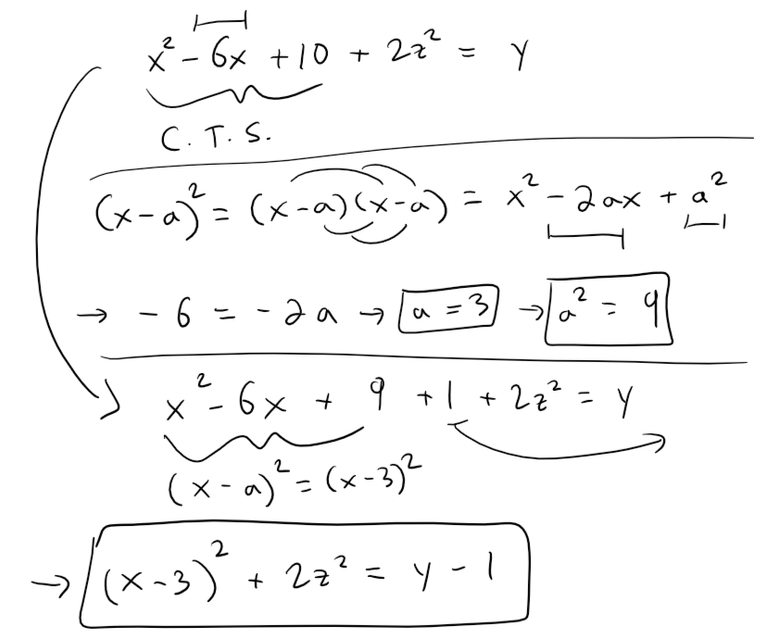
Comparing this equation with Table 1, we see that it represents an elliptic paraboloid.
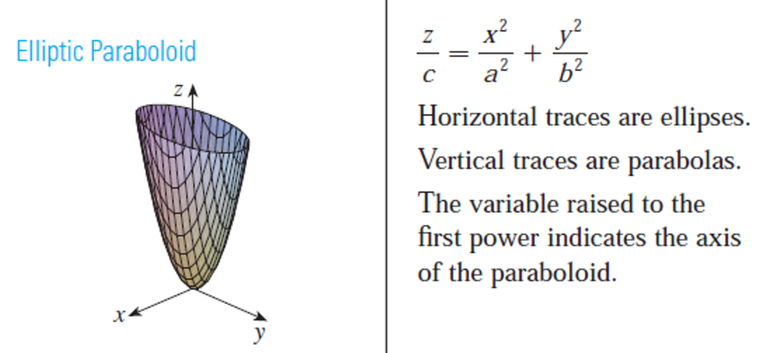
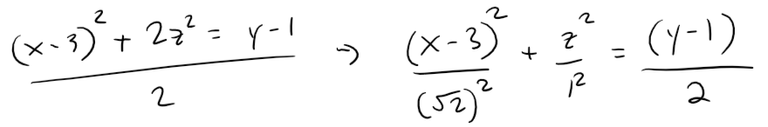
Here, however, the axis of the paraboloid is parallel to the y-axis, and it has been shifted so that its vertex is the point (3, 1, 0).
The traces in the plane y = k (k > 1) are the ellipses:
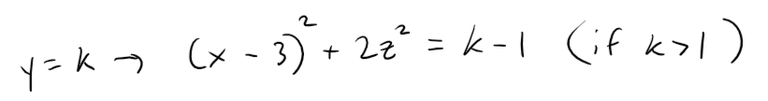
The traces in the xy-plane and the x = 3 plane are the parabolas with equations:
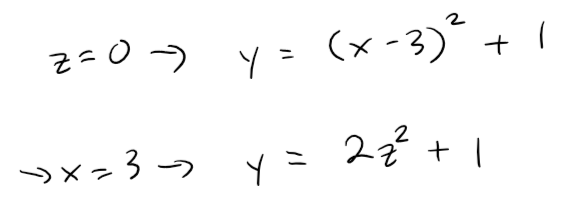
The paraboloid is sketched in the figure below.
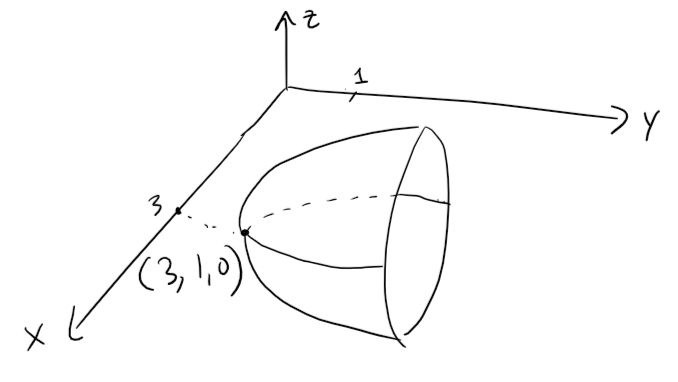
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
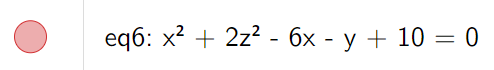
Applications of Quadric Surfaces
Examples of quadric surfaces can be found in the world around us.
In fact, the world itself is a good example.
Although the Earth is commonly modeled as a sphere, a more accurate model is an ellipsoid because the Earth's rotation has caused a flattening at the poles (See Exercise 1).
Circular paraboloids, obtained by rotating a parabola about its axis, are used to collect and reflect light, sound, and radio and television signals.
In a radio telescope, for instance, signals from distant stars that strike the bowl are all reflected to the receiver at the focus and are therefore amplified. (The idea is explained in my earlier video which is briefly explained below).
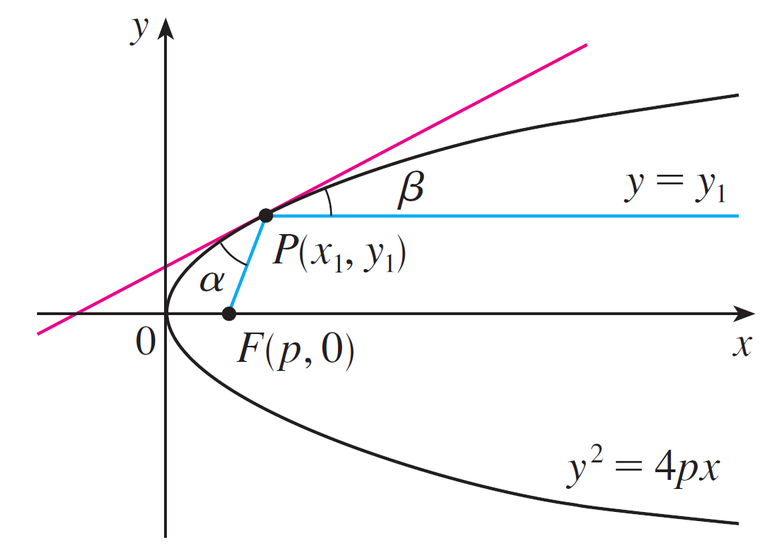
Image: The angles from the focus to any point on a parabola equal each other: α = β
Paraboloids are used as the shape of some automobile headlights and mirrors for telescopes.
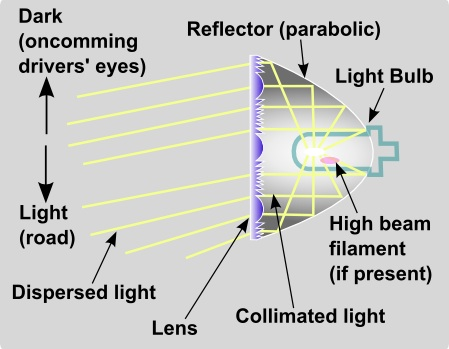

The primary mirror is parabolic, reflecting the parallel rays to the focus. The secondary (flat) mirror redirects this towards the eyepiece.
The same principle applies to microphones and satellite dishes in the shape of paraboloids.

Image: Parabolic microphone
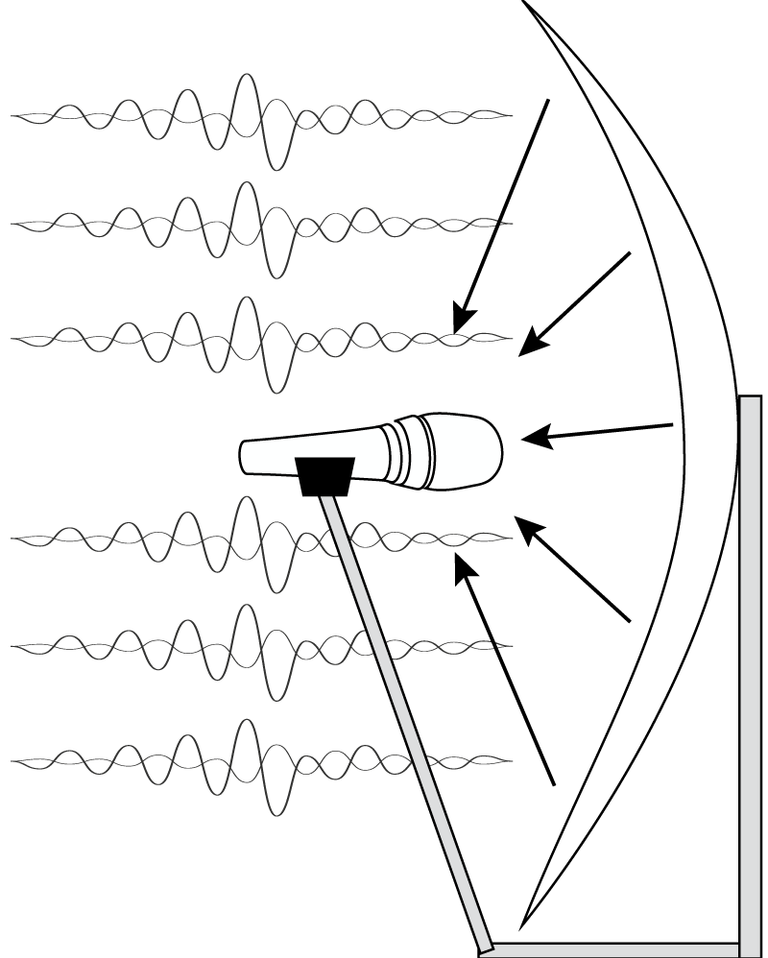

A satellite dish reflects signals to the focus of a paraboloid.
Cooling towers for nuclear reactors are usually designed in the shape of hyperboloids of one sheet for reasons of structural stability.

Nuclear reactors have cooling towers in the shape of hyperboloids.
Pairs of hyperboloids are used to transmit rotational motion between skew axes. (The cogs of the gears are the generating lines of the hyperboloids. See Exercise 2).

Hyperboloids produce gear transmission.
Exercises
Exercise 1: Modeling Earth as an Ellipsoid
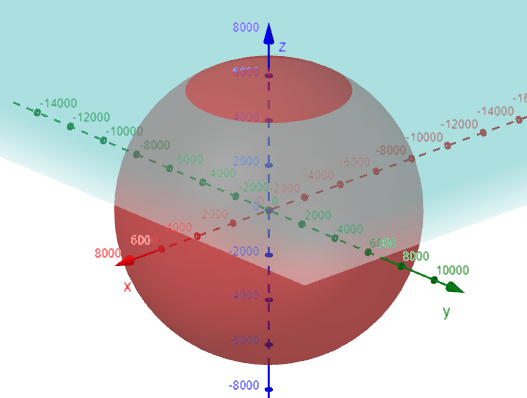
Traditionally, the Earth's surface has been modeled as a sphere, but the World Geodetic System of 1984 (WGS-84) uses an ellipsoid as a more accurate model.
It places the center of the Earth at the origin and the North Pole on the positive z-axis.
The distance from the center to the poles is 6356.523 km and the distance to a point on the equator is 6378.137 km.
(a) Find an equation of the Earth's surface as used by WGS-84.
(b) Curves of equal latitude are traces in the planes z = k.
What is the shape of these curves?
(c) Meridians (curves of equal longitude) are traces in the planes of the form y = mx.
What is the shape of these meridians?
Solution to (a): Earth's Ellipsoid Equation
Recall the equation of an ellipsoid:

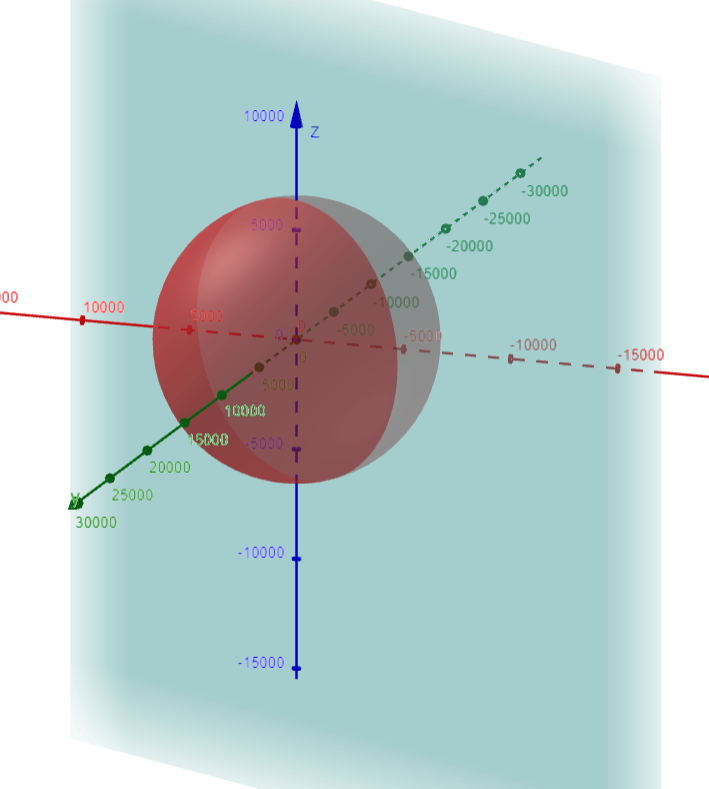
Let's draw the shape of the Earth in 3D.
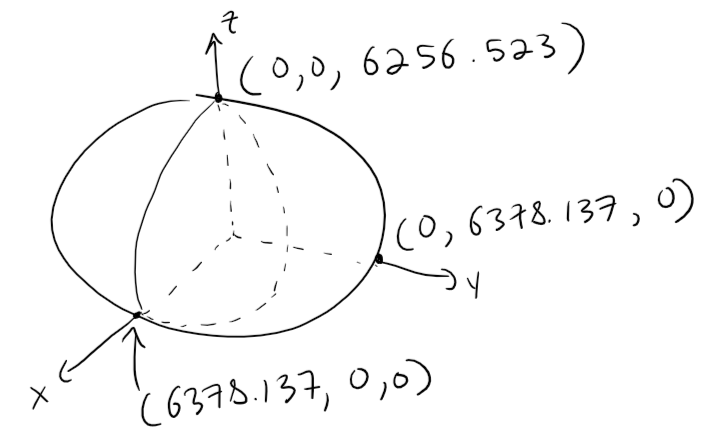
Recall that the parameters a, b, and c of an ellipsoid represent the distance from the center to the edge of the ellipsoid along the x, y, and z axis, respectively.
Thus the equation of the ellipsoid is as follows:
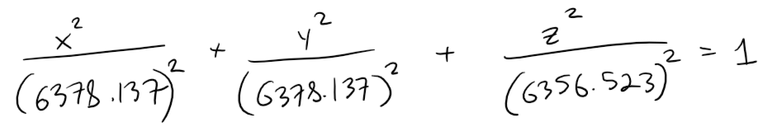
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
Note that we have to zoom out a lot to see the Earth.

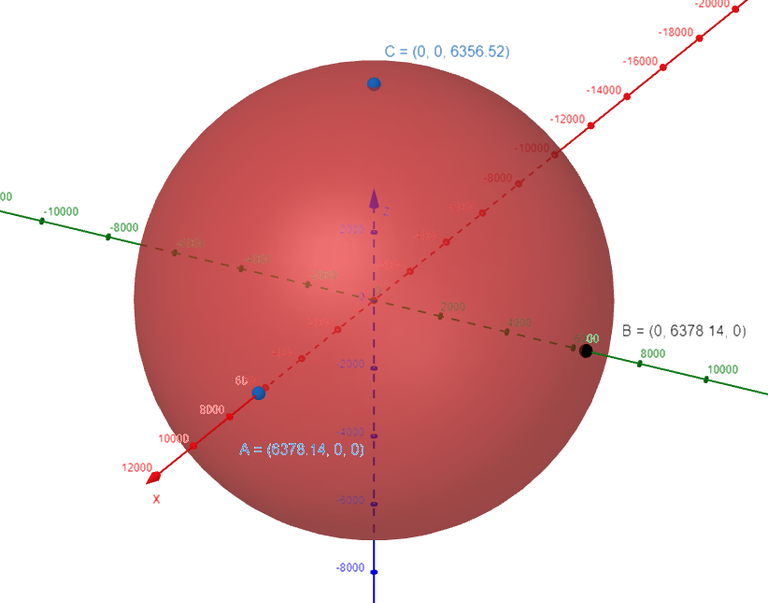
Solution to (b): Parallels or Circular Lines of Equal Latitude
Note that latitude is the vertical angle (φ) and longitude is the horizontal angle (λ) from the center of the Earth.
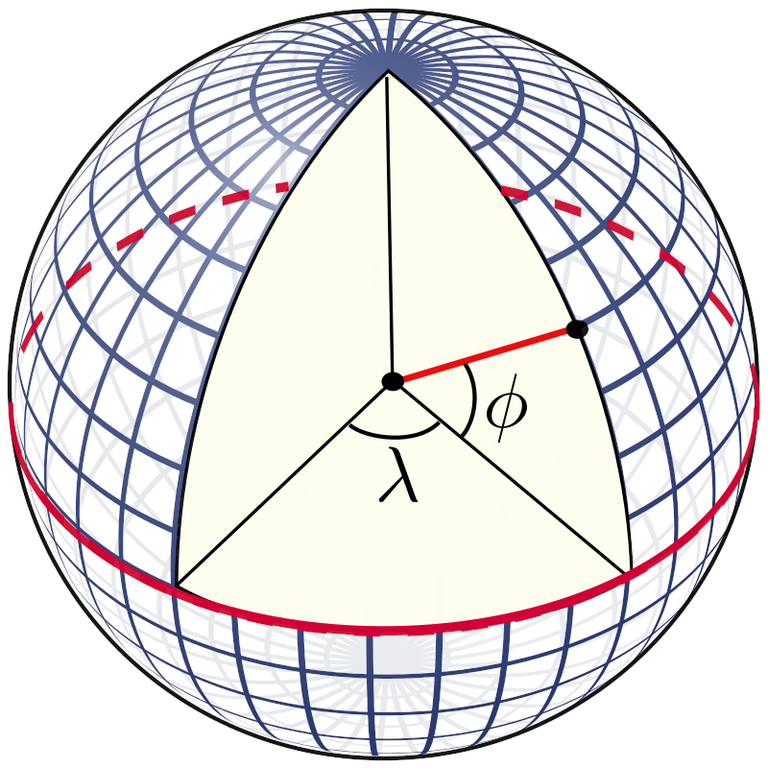
We can determine the curves of equal latitude by setting z = k and finding the traces.
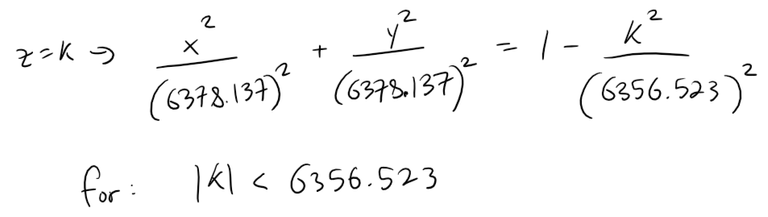
These traces are horizontal circles since the horizonal radii are identical.
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
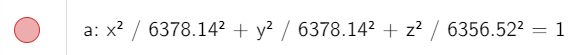
To graph the 2D circles, we need to use the GeoGebra 2D graphing calculator: https://www.geogebra.org/calculator/hte4yr46

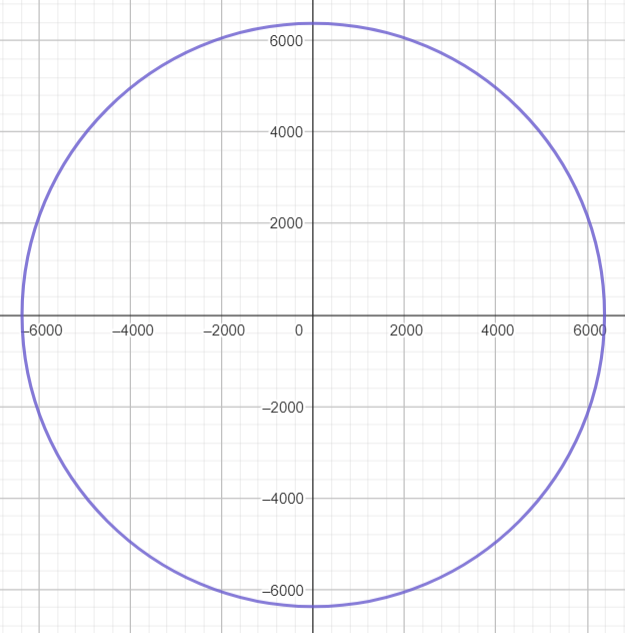
Note that changing the k value makes the circles smaller or bigger as they would appear in 3D viewing vertically away from the poles.
Solution to (c): Meridians or Elliptical Lines of Equal Longitude
The meridians or lines of equal longitude can be determined by setting y = mx and finding the traces.
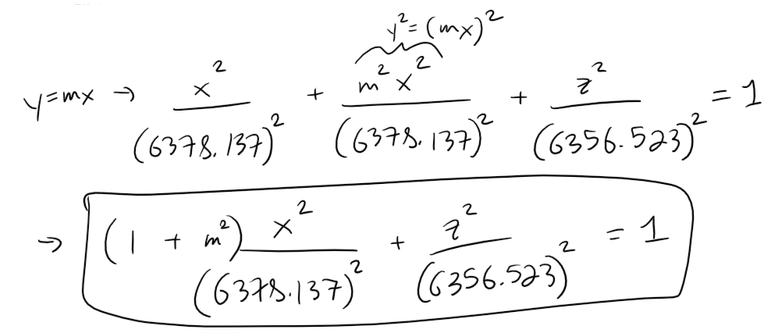
These traces are vertical ellipses since the horizontal and vertical radii are different.
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec
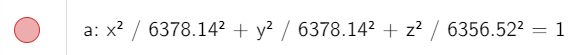

Note that we have to graph with Desmos 2D graphing calculator to obtain the 2D traces (note also that I had to change z to a y for Desmos): https://www.geogebra.org/calculator/hte4yr46

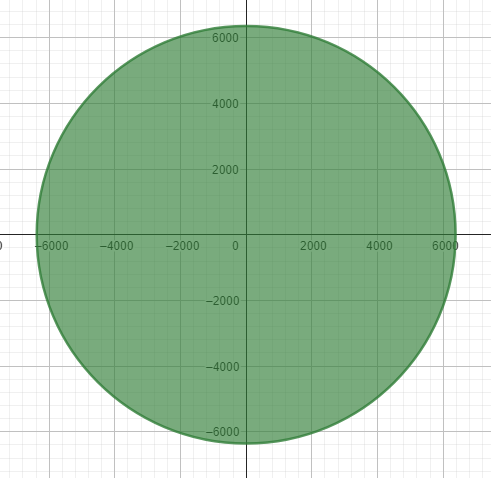
Note also that changing the m value makes vertical ellipses as one would see it looking horizontally at the Earth towards the equator.
Exercise 2: Hyperbolic Paraboloid Generated from Lines
Show that if the point (a, b, c) lies on the hyperbolic paraboloid
z = y2 - x2
then the lines with parametric equations:
x = a + t , y = b + t, z = c + 2(b - a)t
and
x = a + t, y = b - t, z = c - 2(b + a)t
both lie entirely on this paraboloid.
This shows that the hyperbolic paraboloid is what is called a ruled surface; that is, it can generated by the motion of a straight line.
In fact this exercise shows that through each point of the hyperbolic paraboloid there are two generating lines.
The only other quadric surfaces that are ruled surfaces are cylinders, cones, and hyperboloids of one sheet.
Solution:
Recall the equation for a hyperbolic paraboloid.
Recall the Parametric Equations of a Line:

Let's plug in the first set of parametric equations of a line into the given equation of a hyperbolic paraboloid.
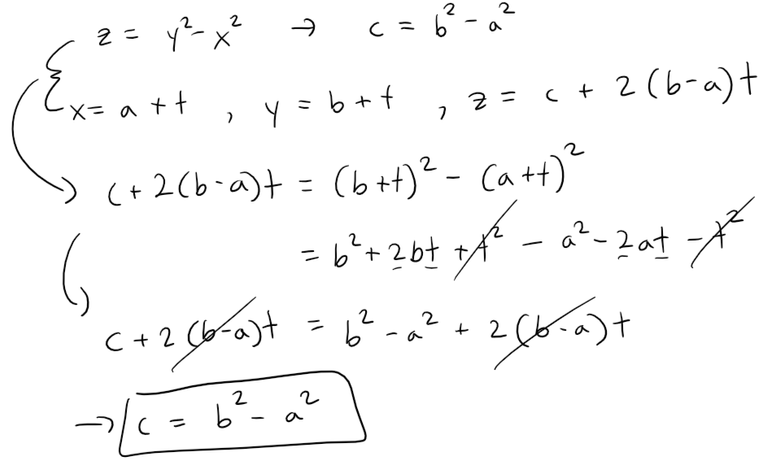
Since the point (a, b, c) is on the hyperbolic paraboloid, then the line is also on it.
Similarly for the other set of parametric equations of a line, we get:

Thus we have two sets of lines on the hyperbolic paraboloid.
Writing the lines in vector form, we can then plot them with GeoGebra.
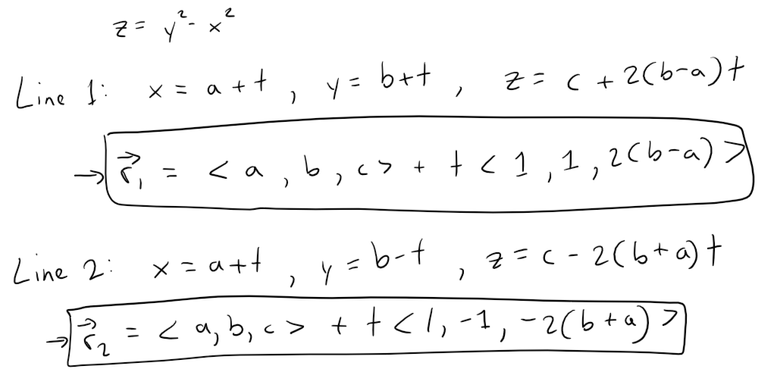
Graphing in GeoGebra: https://www.geogebra.org/3d/tabys4ec

Epic stuff!
¡Enhorabuena!
✅ Has hecho un buen trabajo, por lo cual tu publicación ha sido valorada y ha recibido el apoyo de parte de CHESS BROTHERS ♔ 💪
♟ Te invitamos a usar nuestra etiqueta #chessbrothers y a que aprendas más sobre nosotros.
♟♟ También puedes contactarnos en nuestro servidor de Discord y promocionar allí tus publicaciones.
♟♟♟ Considera unirte a nuestro trail de curación para que trabajemos en equipo y recibas recompensas automáticamente.
♞♟ Echa un vistazo a nuestra cuenta @chessbrotherspro para que te informes sobre el proceso de curación llevado a diario por nuestro equipo.
🥇 Si quieres obtener ganancias con tu delegacion de HP y apoyar a nuestro proyecto, te invitamos a unirte al plan Master Investor. Aquí puedes aprender cómo hacerlo.
Cordialmente
El equipo de CHESS BROTHERS
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.