▶️Watch on 3Speak - Odysee - BitChute - Rumble - DTube - YouTube - PDF notes

In this video I go over how to manually calculate powers 10^0.1, 10^0.2, 10^0.3, ..., 10^0.9 by hand by first using the approximation 10^0.3 = 2. Calculating such powers by hand directly in the same way for multiplication and long division is not possible and requires the use of logarithms or Taylor series. Nonetheless, we can manually approximate such powers by realizing that 10^0.03 is approximately equal to 2 (with an error of -0.24%). This means we can approximate multiples of 10^0.03 by multiplying by 2. For example 10^0.06 is approximately equal to 4. Note that the error becomes double because we multiplied by 2. To get powers such as 10^0.1, we can multiply 10^(0.03 * 7) = 10^2.1 ≈ 2^7 = 128. Then we can divide both sides by 10^2 = 100 to get an approximation 10^0.1 ≈ 1.28. Applying the correction of 7*0.24% we obtain 10^0.1 ≈ 1.2585 which is very close to the actual number 1.2589.

Video inspiration and calculations obtained from the links below:

• Art of Memory article: https://forum.artofmemory.com/t/calculating-10-0-1-0-2-0-3-etc/29957
• OmegaKlass video request: https://www.bitchute.com/video/9tSG173RqQEC/

Timestamps

• Intro: 0:00
• Video request by OmegaKlass: 0:38
• Calculating 10^0.01 by hand: 1:06
• 10^0.3 is approximately equal to 2: 2:28
• 10^0.3 = a number multiplied by itself 10 times equals 1000: 3:13
• Error of 0.24%: 6:30
• Approximating multiples of 10^0.3: 7:17
• Divide by powers of 10 to obtain more powers: 8:53
• Summarizing our simple approximations: 16:54
• Note the pattern: Find multiple of 3 that ends with desired power: 18:34
• Applying the correction (note my voice is when I was sick): 22:10
• Table comparison of approximation and actual values: 27:41
• Outro: 30:01

Playlist

• Calculating by Hand playlist: https://www.youtube.com/playlist?list=PL0919AEF28CB3D765

---

View Video Notes Below!

---

Become a MES Super Fan - Donate - Subscribe via email - MES merchandise

• MES Links webpage - MES Links Telegram - MES Truth

Reuse of my videos:

• Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

• Bookmark sites/channels/accounts and check periodically.
• Remember to always archive website pages in case they get deleted/changed.

Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood

Join my forums: Hive community - Reddit - Discord

Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG

---

NOTE 1: If you don't have time to watch this whole video:

• Skip to the end for Summary and Conclusions (if available)
• Play this video at a faster speed.
  -- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
  -- MES tutorial
• Download and read video notes.
• Read notes on the Hive blockchain $HIVE
• Watch the video in parts.
  -- Timestamps of all parts are in the description.

Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages

---

Video Request

I was asked to make this video by OmegaKlass on Bitchute: https://www.bitchute.com/video/9tSG173RqQEC/

Calculating 10^0.1, 10^0.2, 10^0.3, … , 10^0.9 by Hand

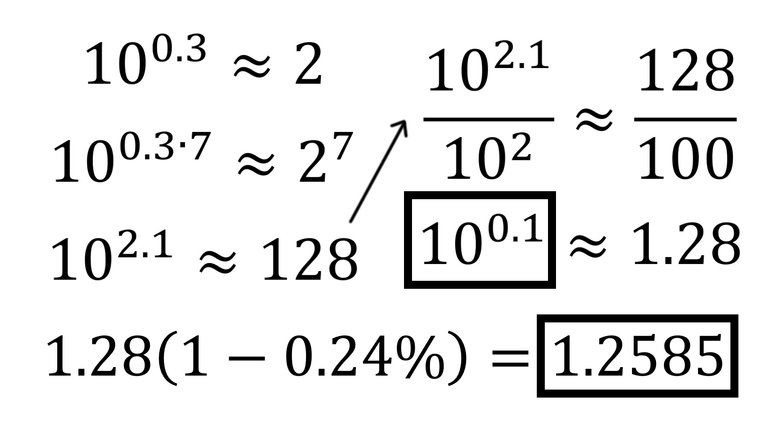
Note that I borrowed a lot from this article: https://forum.artofmemory.com/t/calculating-10-0-1-0-2-0-3-etc/29957

Note also that according to ChatGPT it is not possible to calculate 10^0.1 by hand directly in the same way that we can for division or multiplication.

Let's do a calculation check using my built in OneNote calculator.

10^0 = 1
10^0.1 = 1.2589
10^0.2 = 1.5849
10^0.3 = 1.9953 ≈ 2 = 2¹
10^0.4 = 2.5119
10^0.5 = 3.1623
10^0.6 = 3.9811 ≈ 4 = 2²
10^0.7 = 5.0119
10^0.8 = 6.3096 ≈ 8 = 2³
10^0.9 = 7.9433
10^1 = 10

Note that 10^0.3 is approximately equal to 2. Let's use this for our approximation.

Note also that 10^0.3 means "a number multiplied by itself 10 times and equals 1,000".

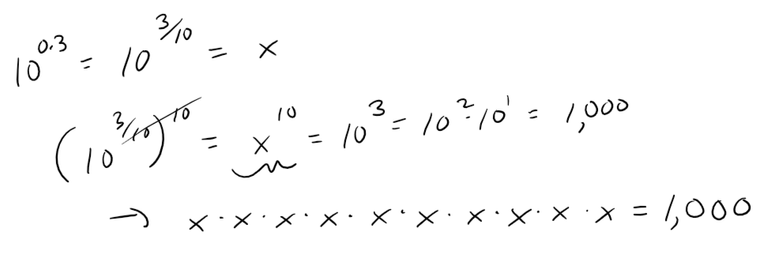
Now back to our approximation.

10^0.3 ≈ 2
2^10 = 1,024

Note the actual value is:

10^0.3 = 1.9953…
1.9953…^10 = 1,000

Thus we have an error of:

(2 - 1.9953) / 1.9953 * 100 = 0.2356% ≈ 0.24%

This means that if we want to be more precise we have to subtract our approximations by 0.24% each time we multiply it.

Let's approximate multiples of 10^0.3:

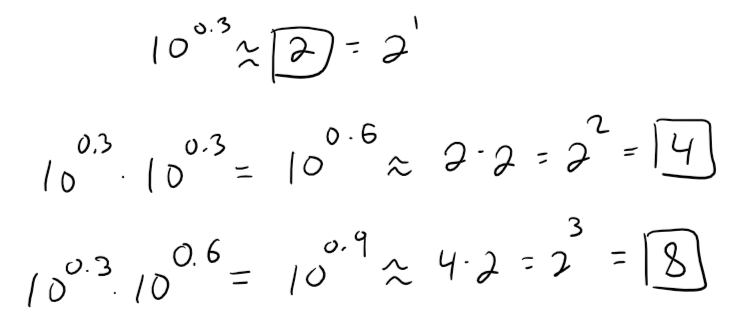
Going further, we can divide by powers of 10 to obtain powers such as 10^0.2:

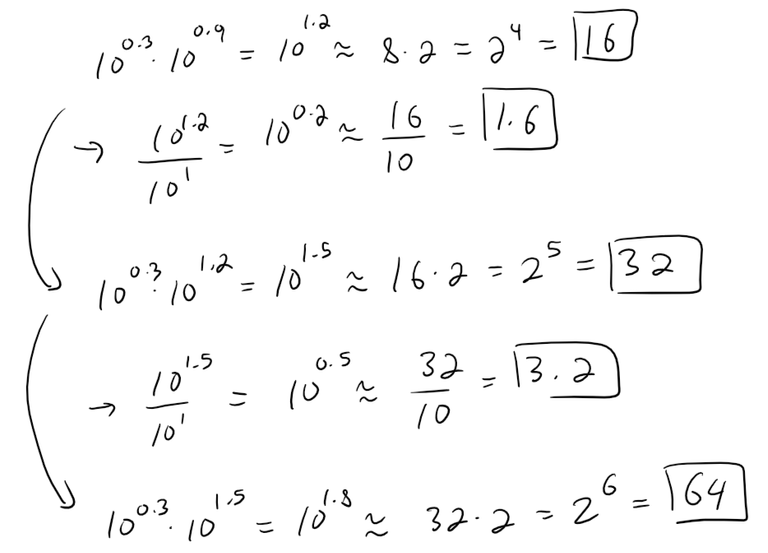
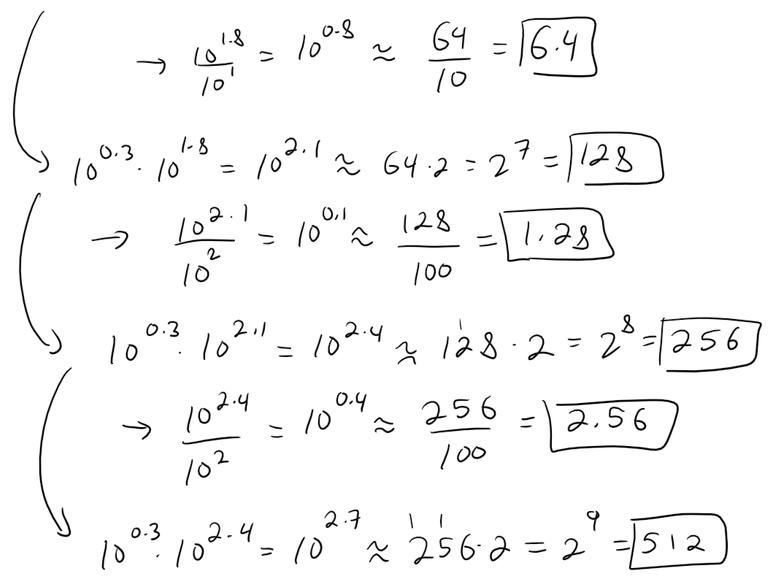
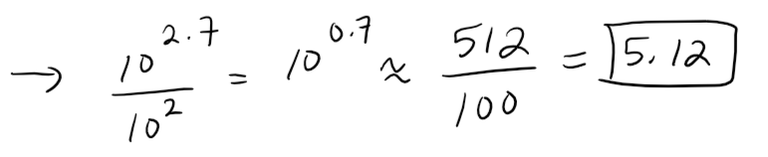
Thus, before we apply our correction, we can summarize our results as follows:

10^0 = 1
10^0.1 ≈ 1.28 (from 10^2.1 ≈ 2^7 = 128)
10^0.2 ≈ 1.6 (from 10^1.2 ≈ 2^4 = 16)
10^0.3 ≈ 2
10^0.4 ≈ 2.56 (from 10^2.4 ≈ 2^8 = 256)
10^0.5 ≈ 3.2(from 10^1.5 ≈ 2^5 = 32)
10^0.6 ≈ 4
10^0.7 ≈ 5.12(10^2.7 ≈ 2^9 = 512)
10^0.8 ≈ 6.4 (from 10^1.8 ≈ 2^6 = 64)
10^0.9 ≈ 8
10^1 = 10

Note the pattern: Find a multiple of 0.3 that ends with the desired number you want:

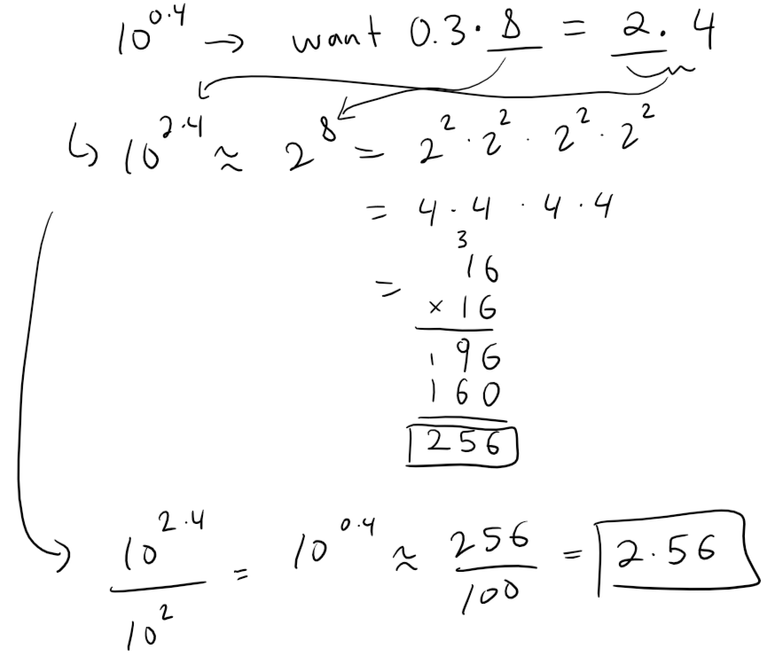
Now to apply the correction. Note that we have to multiply the correction each time we multiply by 2.

Note 1: I am using OneNote's built in calculator for the correction calculations, but you may readily do them by hand or find other tricks outlined in the referenced article to calculate by hand / mentally.

Note 2: I also round up to 0.25% to make the error calculations easier.

10^0 = 1
10^0.1 ≈ 1.28⋅(1 - 7⋅0.24%) = 1.2585 ≈ 1.28⋅(1 - 1.75%) = 1.2576
10^0.2 ≈ 1.6 ⋅(1 - 4⋅0.24%) = 1.5846 ≈ 1.6⋅(1 - 1%) = 1.584
10^0.3 ≈ 2⋅(1 - 0.24%) = 1.9952 ≈ 2⋅(1 - 0.25%) = 1.995
10^0.4 ≈ 2.56⋅(1 - 8⋅0.24%) = 2.5108 ≈ 2.56⋅(1 - 2%) = 2.5088
10^0.5 ≈ 3.2⋅(1 - 5⋅0.24%) = 3.1616 ≈ 3.2⋅(1 - 1.25%) = 3.16
10^0.6 ≈ 4⋅(1 - 2⋅0.24%) = 3.9808 ≈ 4⋅(1 - 0.5%) = 3.98
10^0.7 ≈ 5.12⋅(1 - 9⋅0.24%) = 5.0094 ≈ 5.12⋅(1 - 2.25%) = 5.0048
10^0.8 ≈ 6.4⋅(1 - 6⋅0.24%) = 6.3078 ≈ 6.4⋅(1 - 1.5%) = 6.304
10^0.9 ≈ 8⋅(1 - 3⋅0.24%) = 7.9424 ≈ 8⋅(1 - 0.75%) = 7.94
10^1 = 10

Let's compare our approximations with the exact figures.

	Simple	Correction	Actual
10^0	1	1	1
10^0.1	1.28	1.2585	1.2589
10^0.2	1.6	1.5846	1.5849
10^0.3	2	1.9952	1.9953
10^0.4	2.56	2.5108	2.5119
10^0.5	3.2	3.1616	3.1623
10^0.6	4	3.9808	3.9811
10^0.7	5.12	5.0094	5.0119
10^0.8	6.4	6.3078	6.3096
10^0.9	8	7.9424	7.9433
10^1	10	10	10