Research diaries #4: The beauty of chaos
A while back @alexanderalexis wrote about the beauty of order. So that inspired me to write about the beauty of chaos. In this post I will give an introduction to deterministic chaos.
We will be looking at the logistic map. You can think of this map as describing time evolution of a one dimensional point. Here time moves at discrete steps so time 0, time 1, time 2, time 3 etc. We will be looking at how the position of the point changes of these time steps, this is called its evolution. The logistic has a parameter which we can tweak to generate different evolutions of our point over time. Instead of looking at the whole evolution will be just looking at what the evolution looks like after a long time. We then end up with the image below:
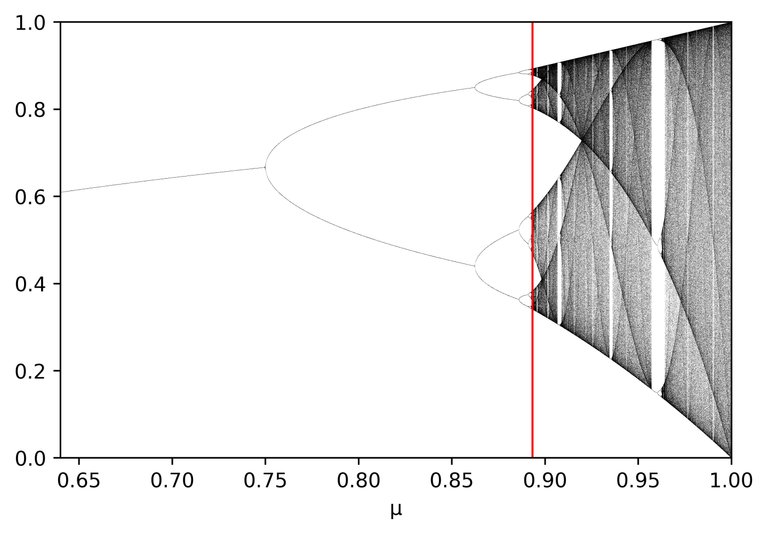
On the x-axis is the parameter, mu, and on the y-axis the evolution. I starts with a single point then as we increase the parameter it doubles we get 2 points for a single parameter, then it doubles again, we get 4 points, then doubles again, 8, then 16, then 32, etc..but then from the red line the points go crazy! We can zoom in a bit and then see what is going on:
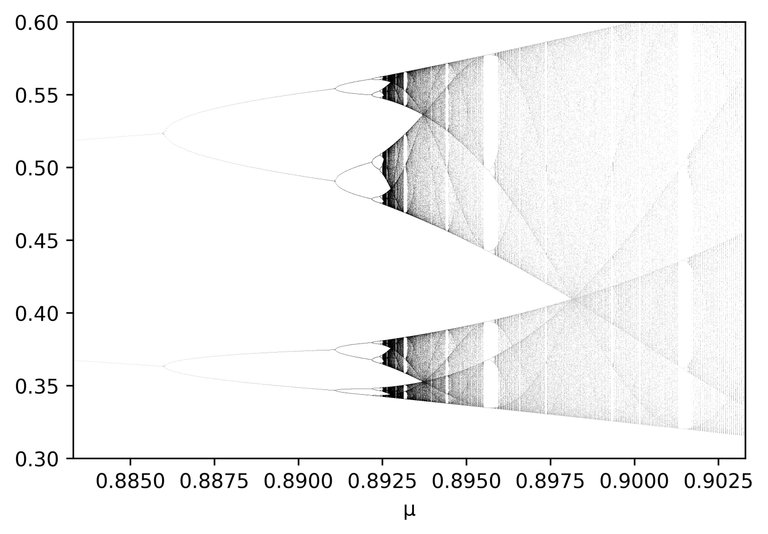
The parameter corresponding to the red line is called the onset of chaos. Not all states beyond this parameter are chaotic. You can see there are parameters where it seems to be filling a line-segment and then suddenly it reduces to a couple of points. It seems to be fairly unpredictable what state corresponds to which parameter.
What is chaos?
So how to identify chaos? Informally, points which start very close exhibit different behaviour as time passes. In the image below we follow the chaotic evolution of two points which start very close to each other. We observe that for about the first 10 time steps they look very similar by then over time evolution 1 and evolution 2 behave completely different.
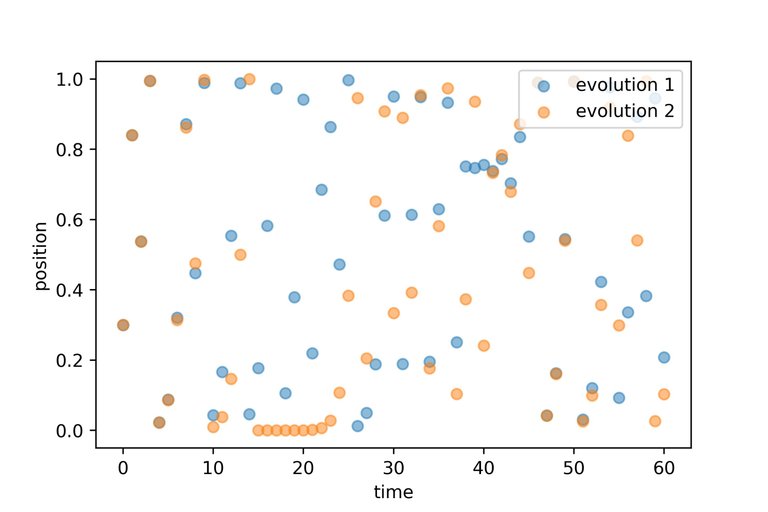
The evolution of a single point is deterministic. Meaning that the past determines all future positions of the point. Chaos here means that an inexactness in determining the starting position will yield a completely different evolution. Quoting Lorenz, the father of deterministic chaos,
Chaos: When the present determines the future, but the approximate present does not approximately determine the future. source
What is the driving mechanics of chaos?
We look at the mu=1 case. We graph the state at time t against the next state at time t+1. If we study what happens to the curve projected on the x-axis versus the y-axis we see that the curve gets stretched and folded. The stretching makes sure that points which are close to each other will move away from each other and the folding makes sure that the points don't run off to infinity.
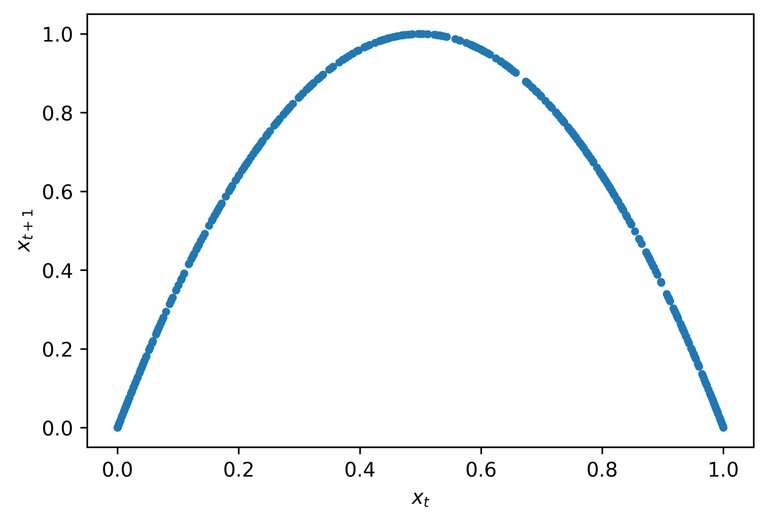
In conclusion
The logistic map is a toy model. There are many more complicated systems that exhibit chaos. A famous example is the butterfly attractor in the Lorenz system. The Lorenz system is derived from a weather-type model. So probably it comes as no surprise that in weather modelling chaos plays an important role. To me it is remarkable that chaos underlying complicated weather models can be captured by something as simple as the equations for the logistic map. But this is one of the marvels of math: a couple lines of equations can contain a whole theory.
Cat tax

At first I noticed one umbrella/beach ball top/broken spiderweb shape, but then I noticed two more. Is it a fractal chaos if time is extended… like x 1000 more time increments?
I guess with time increments you mean the parameter mu? Yes if you choose a finer grid the complexity persists. The second picture is a bit similar to the first eventhough we are zooming in. So it has fractal properties. ^^
Do you mind detailing more the mechanism behind the splitting of one points into two? How does that work here?
With splitting you mean what happens directly after mu \approx 0.75?
I am plotting the orbit. So denote the logistic map by f_\mu. And what I plot is the set { f^n(x_0) : n \in N, n> big number } for x_0=1/2. So after \mu \approx 0.75 the orbit is an attracting period-2 orbit.
I am not sure if that answers your question :3
I am not sure too but I think that I got it (as you insisted on the orbit). Thanks!
I think you want to know how to determine the bifurcation at mu=0.75?
So f_mu has two fixed points. One at 0 and one at (-1+4mu)/(4mu). The single line up to mu=0.75 follows (-1+4mu)/(4mu) because it is a stable fixed point. Then at mu=0.75 we have that f_\mu'(-1+4mu)/(4mu)=-1 and for mu>0.75 we have that |f_\mu'(-1+4mu)/(4mu)|>1 so it becomes unstable.
If you investigate the map f_mu \circ f_mu you see that two fixed points are being "created" as we pass mu=0.75. For the original map f_mu the fixed points of f_mu \circ f_mu correspond to a period 2-orbit.
This transition is called a transcritical bifurcation because the stability of the fixed point at (-1+4mu)/(4mu) changes.
There is this user that use to write about chaos consistently in the past. I can't really recall his username now but certain you will find his post interesting.
The cat looks calm though, a complete antithesis.
Ah yes I remember him but also forgot his username. We almost got into a fight :3
🤣
Thanks for the mention!
Post a bit math-heavy for me, but I'm slowly working to fix that. A very long-term project!
The butterfly attractor you mention - is that the butterfly effect? It certainly reminds me of it, small initial differences or inexactness leading to large differences in the future.
You are welcome ^^
If you need help with math let me know :D
The butterfly in the Lorenz system refers to the shape of the chaotic attractor which looks like a butterly. The story about the butterfly wings that make a small initial differences or inexactness which then causes hurricane is not why the butterfly attractor is called the butterfly attractor. However the phenomenon driving the butterfly story is what drives the chaos in the butterfly attractor.
I hope that wasn't too confusing :3
Loved maths until they hit me with the one called further mathematics....the story changed.
Maths is actually interesting.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more
Fascinating! And I thought chaos was just something that happened in my life! lol
I am not a math or theoretical thinker, but your narrative was quite illuminating. I respect the kind of minds that can both understand and relate their knowledge.
Thanks for sharing this expose on chaos...
Wishing you happiness, health, and prosperity in 2022!
Cheers!
Thanks for stopping by :3
The 40k chaos gods approve your illumination

Best wishes for the new year ^^