Positions in different dimensions

Shoutout to Wikipedia

In this article you will find

• Introduction
• How to represent a position?
• Cartesian System
• Polar and Cylindrical Coordinates
• Spherical Coordinates

Greetings to all. I apologize for not being as present this week on Hive as I would have liked. This is due to different obligations related to my career, such as robotics and microprocessor applications subjects, which have taken up most of my time.

However, this is not all bad news. Because of these subjects, I have much more knowledge and topics to present to you.

Today I would like to talk to you about a topic a little further from the programming we are used to. In this case, we will go back to the basics in a way and add a more precise touch: Representation in space.

You see, when you work with automatable elements such as robots, for which we must specify the position and orientation of an object if we want it to manipulate it effectively, we must know how to represent this data in a way that our device understands.

It is here that the use of mathematical methods allows us to obtain precise data about our final goal, that the robot works appropriately with the object.

It is from this need that in the following article we will talk about the different ways of representing the position of an object in space, limiting ourselves for now to 2 and 3 dimensions, increasing them in case the demand for this type of content increases.

Now, without further ado:

Let's get started!

How to represent a position?

Shoutout to

When representing a body in space, we must take into account the number of dimensions of the plane in which it is located, but what is a plane?

A plane is used to represent a dimensional space, which can have different dimensions, where axes are used to represent distance in these dimensions.

For example, if we take into account the most common type of plane, a Cartesian plane, we can see that we have two axes, the x axis and the y axis. Each axis is equivalent to one dimension, so we can safely say that this plane has two dimensions.

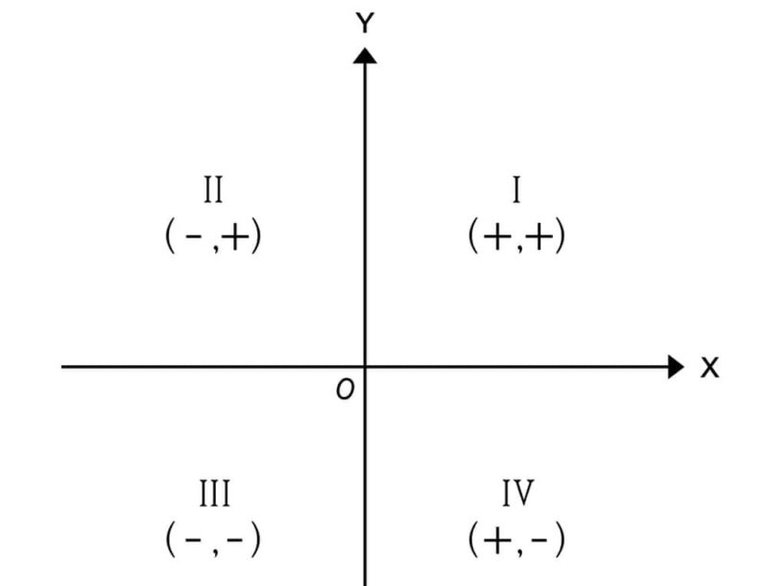
Shoutout to Concepto

Now, if we wanted to represent a body in this space, we only have to know the x and y coordinates to plot it on the graph. However, as the dimensions increase, so does the number of axes to take into account. If we see a three-dimensional plane:

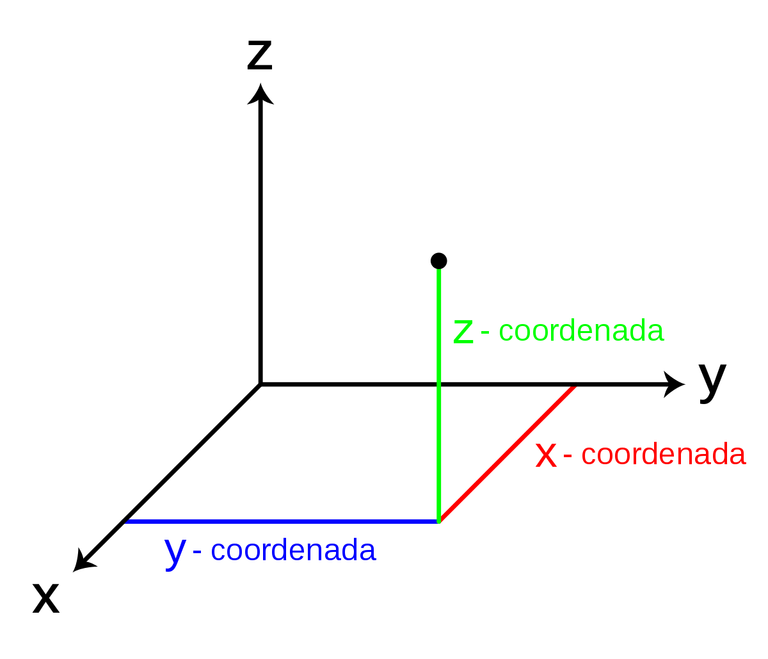
Shoutout to Wikipedia

Now we will have to take into account not only x or y, but also z in order to plot a position at some point.

These values that denote the position on an axis (x,y,z...) are called components and according to the number of dimensions, they will also increase.

Now that we know this, we can move on to denote different systems to represent positions in space.

Cartesian System

Shoutout to Math Insight

Due to its simplicity, this is usually the type of graph commonly used in the study of basic mathematics. To represent this, you only need two axes, which are perpendicular to each other, taking two components, which are x,y.

These axes are usually represented by vectors, which are line segments with a specific direction. We can assimilate these to the figure of an arrow.

Now, we can say that because we have two components (Two dimensions), then we will use two vectors to represent each axis.

The point where these two axes connect is what we know as the origin, which will be the point from which the representation of the position begins. For example, if you wanted to know how far an object is from your body, then your body would be the origin.

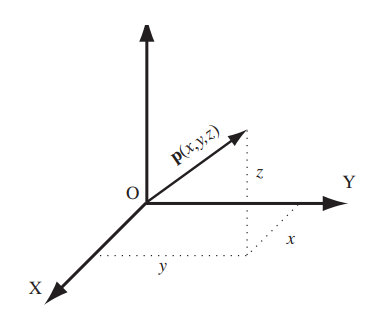
Now, as I had mentioned previously, if we wanted to represent a point in the space of this axis, we only have to plot it taking into account the units and values of the x axis. This position is also represented by a vector, which starts from the origin and ends at the point we want to plot.

It is precisely the values of x and y of this vector that we will call Cartesian coordinates, allowing the extreme of this vector to be represented as p(x,y)

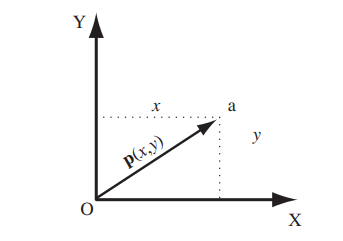
Now, we have seen how this vector is drawn in two dimensions, but what would it be like if we added another dimension?

In order to represent the vector, we add a third coordinate corresponding to the z axis, where if we want to find the end of the vector, we first join the points of the x and y axis, and from this we plot the position on the z axis (In this case with orientation vertical), and then join the end, as seen in the figure.

Polar Coordinates and Cylindrical Coordinates

Shoutout to Paul's Online Math Notes

Cartesian coordinates will not be the only way in which we can represent a position vector, since in certain cases, it will be much more helpful to take into account parameters such as the angle of a specific position.

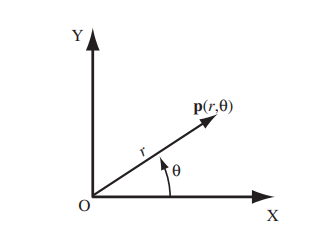
To meet this need, we use the representation for polar coordinates, where we replace the x and y positions of the Cartesian coordinates with the values of:

• The distance from the origin (0) to the end of the vector p, represented as r.
• The angle measured from the x-axis to the vector, known as theta (θ).

Thus, if we want to know the angle and measure the distance from the origin to the desired point in a single magnitude, we would use polar coordinates.

Now, if the number of dimensions increases to three, we must change the polar coordinates for another representation system.

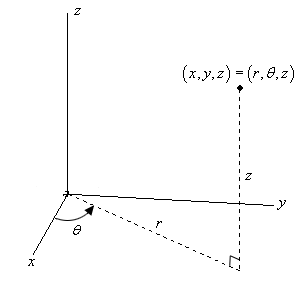
In this case, cylindrical coordinates can be used, which receive their name because their components can describe a cylindrical shape (two Cartesian motion, one rotation).

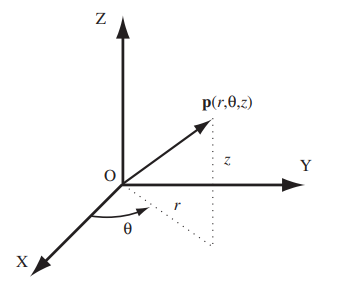
Thus, the only thing that changes with respect to polar coordinates is that because there is an extra dimension, there will also be an additional component, represented by z.

To describe the vector taking into account z, a combination of polar and Cartesian coordinates is used, where the distance from the origin to the end of the vector at x,y is described along with the angle of the vector to x.

Then, at the end of the vector at x,y, we begin measuring in the direction of the z axis (in this case, vertical again), and once we reach the desired point, we draw the vector.

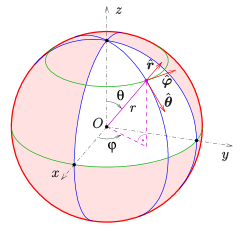
Spherical Coordinates

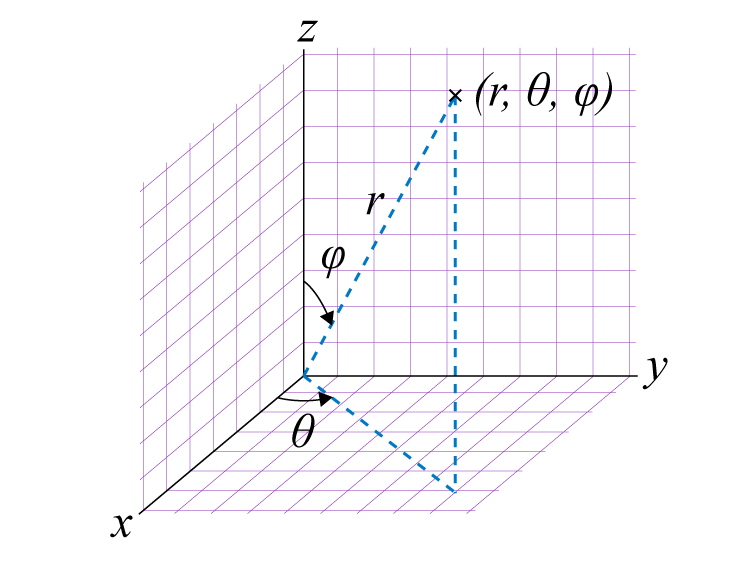
Shoutout to BYJU'S

Another way to locate a vector in a three-dimensional space. The changes of this with respect to the cylindrical coordinates are reduced to the third component, which instead of being z, will be another angle, determined by phi(Φ). Phi represents the angle measured from the z axis to the vector.

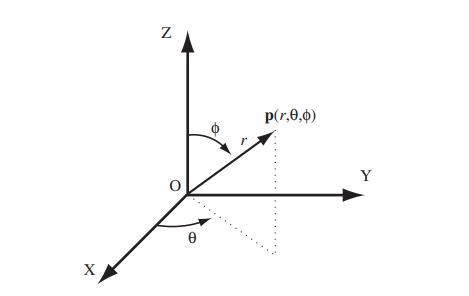
Thus, if we wanted to plot a vector in three dimensions using spherical coordinates:

• We would take into account the given data starting with the theta angle to plot it towards a point that coincides with the origin.
• We begin to outline the straight line with a distance of r so that it coincides with the angle of theta.
• Once the line r is outlined, we draw another line oriented to the z axis from the end with the same length.
• We draw the vector taking into account the angle z and we would have our representation.

I hope this post has provided you with more than one way to represent positions in space.

These techniques will not only serve to represent positions, since with some of the systems mentioned you will be able to obtain interesting data, such as the phase shift angle of an alternating current line as well as the behavior of the functions.

In this way, I encourage you to practice assigning any value to the components and plotting the vector based on them.

However, in this case, the position will not be enough to give a robot the data it wants to work with an object, since we also have to indicate the orientation. If you want an article on orientation, just let me know.

Thank you for your support and good luck!

Posiciones en distintas dimensiones

Shoutout to Wikipedia

En este artículo encontrarás

• Introducción
• ¿Cómo representar una posición?
• Sistema Cartesiano
• Coordenadas Polares y Cilíndricas
• Coordenadas Esféricas

Un saludo a todos. Me disculpo por no estar tan presente esta semana en Hive como me hubiera gustado. Esto se debe a distintas obligaciones relacionadas a mi carrera, como lo son las asignaturas de robótica y aplicaciones con microprocesadores, que han tomado la mayor parte de mi tiempo.

Sin embargo, esto no son todas malas noticias. Debido a estas asignaturas, tengo mucho más conocimiento y temas que presentarles.

En el día de hoy quisiera hablarles sobre un tema un poco más alejado de la programación a la que estamos acostumbrados. En este caso, volveremos en cierto modo a lo básico y le añadiremos un toque más preciso: La representación en el espacio.

Verás, cuando trabajas con elementos automatizables como robots, a los cuales debemos especificar la posición y la orientación de un objeto si queremos que lo manipule de manera efectiva, debemos de conocer como representar estos datos de forma que lo entienda nuestro dispositivo.

Es aquí, que el uso de métodos matemáticos nos permiten obtener datos precisos sobre nuestra meta final, que el robot trabaje de manera adecuada con el objeto.

Es de esta necesidad, que en el siguiente artículo hablaremos sobre las distintas formas de representar la posición de un objeto en el espacio, limitándonos por ahora a 2 y 3 dimensiones, aumentándolas en caso de que la demanda por esta clase de contenido aumente.

Ahora, sin más que decir:

¡Comencemos!

¿Cómo representar una posición?

Shoutout to

Al representar un cuerpo en el espacio, debemos de tomar en cuenta la cantidad de dimensiones del plano en que se encuentre, pero ¿Qué es un plano?

Un plano es usado para representar un espacio dimensional, el cual puede tener diferentes dimensiones, donde se usan ejes para representar la distancia en estas dimensiones.

Por ejemplo, si tomamos en cuenta el tipo más común de plano, un plano cartesiano, podremos ver que tenemos dos ejes, el eje x y el eje y. Cada eje equivale a una dimensión, por lo que podemos decir con seguridad que este plano tiene dos dimensiones.

Shoutout to Concepto

Ahora bien, si quisieramos representar un cuerpo en este espacio, solo tenemos que saber las coordenadas x y y para trazarlo en la gráfica. Sin embargo, a medida que aumentan las dimensiones, también lo hacen la cantidad de ejes a tomar en cuenta. Si vemos un plano de tres dimensiones:

Shoutout to Wikipedia

Ahora tendremos que tomar en cuenta no solo a x o y, sino también a z para poder trazar una posición en algún punto.

Estos valores que denotan la posición en un eje (x,y,z...) reciben el nombre de componentes y de acuerdo a la cantidad de dimensiones, también aumentarán.

Ahora que sabemos esto, podemos pasar a denotar distintos sistemas para representar posiciones en el espacio.

Sistema Cartesiano

Shoutout to Math Insight

Debido a su simplicidad, este suele ser el tipo de gráfico usado comúnmente en el estudio de las matemáticas básicas. Para representar este, solo hacen falta dos ejes, los cuales se encuentran perpendiculares entre si, tomando dos componentes, los cuales son x,y.

Estos ejes suelen representarse por medio de vectores, los cuales son segmentos de recta con una dirección específica. Podemos asimilar estos a la figura de una flecha.

Ahora bien, podemos decir que debido a que tenemos dos componentes (Dos dimensiones), entonces usaremos dos vectores para representar cada eje.

El punto donde estos dos ejes se conectan es a lo que conocemos como origen, que será el punto desde el cual se comienza a hacer la representación de la posición. Por ejemplo, si quisieras saber a que distancia se encuentra un objeto de tu cuerpo, entonces tu cuerpo sería el origen.

Ahora bien, como había mencionado anteriormente, si quisieramos representar un punto en el espacio de este eje, solo tenemos que trazarlo tomando en cuenta las unidades y los valores del eje x. Esta posición también es representada por un vector, el cual comienza desde el origen y finaliza en el punto que queremos trazar.

Es precisamente a los valores de x y y de este vector a los que llamaremos coordenadas cartesianas, permitiendo representar el extremo de este como p(x,y)

Ahora bien, hemos visto como se traza este vector en dos dimensiones, ¿Pero como sería si agregamos otra dimensión?

En orden de representar el vector, añadimos una tercera coordenada correspondiente al eje z, donde si queremos encontrar el extremo del vector, unimos primero los puntos del eje x y y, y partiendo de este trazamos la posición en el eje z (En este caso con orientación vertical), para luego unir el extremo, como se observa en la figura.

Coordenadas Polares y Coordenadas Cilíndricas

Shoutout to Paul's Online Math Notes

Las coordenadas cartesianas no serán la única forma en la que podremos representar un vector de posición, puesto que en ciertos casos, nos vendrá de mucha más ayuda tener en cuenta parámetros como el ángulo de una posición específica.

Para suplir esta necesidad, usamos la representación para coordenadas polares, donde reemplazamos las posiciones x y y de las coordenadas cartesianas por los valores de:

• La distancia desde el origen (0) hasta el extremo del vector p, representada como r.
• El ángulo medido desde el eje x hasta el vector, conocido como theta (θ).

Así, si queremos saber el ángulo y medir la distancia del origen al punto deseado en una sola magnitud, usaríamos las coordenadas polares.

Ahora bien, si aumenta el número de dimensiones a tres, debemos de cambiar las coordenadas polares por otro sistema de representación.

En este caso, pueden usarse las coordenadas cilíndricas, que reciben su nombre debido a que sus componentes pueden describir una forma cilíndrica (Dos de movimiento cartesiano, una de rotación).

Así, lo único que cambia con respecto a las coordenadas polares es que debido a que hay una dimensión extra, también se tendrá una componente adicional, representada por z.

Para describir el vector tomando en cuenta z, se usa una combinación de las coordenadas polares y cartesianas, donde se describe la distancia del origen al extremo del vector en x,y junto con el ángulo del vector a x.

Luego, en el extremo del vector en x,y se comienza a medir en dirección del eje z (En este caso, de nuevo vertical), y una vez se llega al punto deseado, trazamos el vector.

Coordenadas Esféricas

Shoutout to BYJU'S

Otra forma de localizar un vector en un espacio de tres dimensiones. Los cambios de esta con respecto a las coordenadas cilíndricas se reducen al tercer componente, que en vez de ser z, será otro ángulo, determinado por phi(Φ). Phi representa el ángulo medido desde el eje z hasta el vector.

Así, si quisieramos trazar un vector en tres dimensiones usando las coordenadas esféricas:

• Tomaríamos en cuenta los datos dados empezando con el ángulo theta para trazarlo hacia un punto que coincida con el origen.
• Comenzamos a delinear la línea recta con una distancia de r de forma que coincida con el ángulo de theta.
• Una vez que se tenga la línea r delineada, trazamos otra recta con orientación al eje z desde el extremo con la misma longitud.
• Trazamos el vector tomando en cuenta el ángulo z y tendríamos nuestra representación.

Espero que este post te haya provisto de más de una manera de representar posiciones en el espacio.

Estas técnicas no solo servirán para representar posiciones, puesto que con algunos de los sistemas mencionados podrás obtener datos interesantes, como lo es el ángulo de desfasaje de una línea de corriente alterna así como el comportamiento de las funciones.

De esta forma, te animo a practicar asignando cualquier valor a las componentes y trazando el vector en base a estas.

Sin embargo, en este caso, la posición no será suficiente para darle a un robot los datos que quiere para trabajar con un objeto, puesto que también tenemos que indicarle la orientación. Si quieres un artículo sobre la orientación, solo déjamelo saber.

¡Gracias por tu apoyo y buena suerte!