math on steroids

Shoutout to EDUCBA

In this article you will find:

• Introduction
• What is NumPy?
• Creating Arrays with NumPy
• Arrays
• Some array operations in NumPy

As programmers, when using Python we are constantly working with arrays and matrices, applying mathematical functions and different procedures to obtain the result we want. However, there is a limit to what we can do in the 'vanilla' version of Python.

Even if with modules like math we can increase the range of functions to be carried out, this still falls short. This is why mathematicians and scientists who use this programming language for their research often turn to one of the most popular Python libraries: numPy.

From working with matrices to applying linear algebra and Fourier transforms, if you want to check your calculations and do really interesting things, numPy will be your best option.

If you want to learn what this library is, how to use it and its true potential, you just have to continue reading the articles in this new arc in Coding Basics.

Let's get started!

What is NumPy?

Shoutout to freeCodeCamp

NumPy is an open source library for the Python language, created in 2005 by Travis Oliphant. From the beginning, it caught the attention of the Python community by allowing the user to create array objects that responded 50 times faster to their queries.

This is possible because the arrays are stored in a continuous memory location, which the program can easily access.

Thanks to the contribution of its creator and a large number of users, NumPy can now carry out a large number of complex operations such as:

• Calculate Binomial Distribution.
• Work with trigonometric, logarithmic and hyperbolic functions.
• Use Fourier Series.

This is just a primer on what people can do with numPy, like handwritten number recognition systems, fraud detectors, and many other things.

In order to make learning numPy more enjoyable, in the first article we will see the arrangements, a fundamental part of the charm of numPy. These arrays are not limited to a few dimensions like regular lists and tuples in Python, but we can determine the dimensions we want and perform countless operations on them.

That said, how can we create arrays with NumPy?

Creating Arrays with numPy

Shoutout to Learn with Alf

Before we can work with arrays in numPy, we must make sure we have this package installed. As always, if you don't have a python package you want to use, just install it by going to the command line, making sure pip is installed, and then using the command:

>>> pip install [name of the library]

In this case, since we want to install NumPy:

>>> pip install numpy

We use this and wait a few seconds, once the installation process is finished, we will be able to use numpy in our programs as long as we remember to import this library:

import numpy

Now, if we want to create an array with numpy, we would only have to use the .array function to create an object of type ndarray, whose content we can observe:

import numpy

array = numpy.array([1,2,3,4,5])

print(array)
print(type(array))

If we run the program:

>>>
[1 2 3 4 5]
<class 'numpy.ndarray'>

Another really flexible feature of NumPy is that we not only have to introduce lists to create arrays, but we can also use sets and tuples:

import numpy

array = numpy.array([1,2,3,4,5])

print(array)
print(type(array))

>>>
[1 2 3 4 5]
<class 'numpy.ndarray'>

Before we can perform array operations, we must take a class on the basics of arrays and their dimensions.

Arrays

Shoutout to Indian AI Production

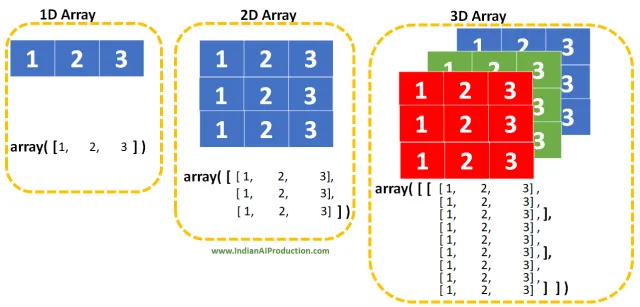
As we know, arrays are a collection of data ordered in a single variable, these can contain an endless number of numbers, strings and many other data that we can use to our advantage.

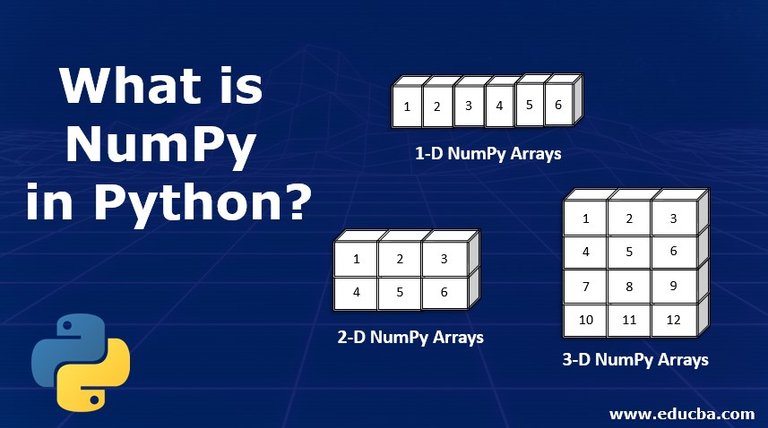
However, until now we have only known two types of arrangements, 0-D and 1-D. What are these strange numbers? Well, let me explain:

0-D Arrays

Going back to physics a little, 0-D arrays are scalars, that is, those values that only have amplitude, magnitude or size, that is, one value. These scalars are the variables that we encounter on a daily basis with only one value:

x = 2

If we wanted to create a 0-D array with numpy, we just have to follow the same procedure, placing a single value in the array function:

import numpy

array = numpy.array(55)

print(array)
print(type(array))

>>> 55

1-D Arrays

The types of arrangements we are used to. A 1-D or one-dimensional array is simply an array that contains 0-D arrays. These can be lists of numbers, sets, tuples and many others. For example:

import numpy

array = numpy.array([55,56,57,58,59])

print(array)
print(type(array))

>>> [55 56 57 58 59]

2-D Arrays

As we increase dimensions, we notice a pattern. An arrangement of a given dimension will always have within it arrangements of a smaller dimension.

This rule still applies to 2-D arrays, which are arrays that contain 1-D arrays as their elements. They can also be used to represent matrices since they follow a structure similar to the column/row used by them, with nested arrangements. Watching it:

import numpy

arr = numpy.array([[3, 3, 3], [3, 3, 3]])

print(arr)

>>>
[[3 3 3]
  [3 3 3]]

3-D Arrangements

Following tradition, 3-D arrays have 2-D arrays as their elements:

import numpy

arr = numpy.array([[[3, 3, 3], [3, 3, 3]],[[3, 3, 3], [3, 3, 3]]])

print(arr)

>>>
[[[3 3 3]
   [3 3 3]]

  [[3 3 3]
   [3 3 3]]]

This will continue for each dimension, where if we want to check the dimension of an array we only have to use the ndim method:

print(array.ndim())
>>> 3

If we want to create arrays of larger dimensions (4,5,6, etc...), we can do it manually, a really tedious process, or assign the number of dimensions through another parameter, known as ndmin or number of dimensions. If, for example, we wanted to create an 8-dimensional array, we do the following:

import numpy

arr = numpy.array([[[3, 3, 3], [3, 3, 3]],[[3, 3, 3], [3, 3, 3]]], ndmin=8)

print(arr)

>>>
[[[[[[[[[3 3 3]]
        [3 3 3]]

       [[3 3 3]
        [3 3 3]]]]]]]]

Some operations with arrays in NumPy

Shoutout to Towards Data Science

Like Python's own arrays such as lists, sets and tuples, we can perform a series of operations on the arrays created with numpy. Among these we have:

Indexing (Index Access)

A very common operation in arrangements where the order of the elements matters. If we want to access one of the elements of a list that we create, all we have to do is place the list and in brackets the number of the index where the element is located:

list[index]

This will be exactly what we will do with the arrays created by numpy, where we just put the element number and access it. Example:

import numpy

array = numpy.array([1,2,3,4,5])

print(array[0])

>>> 1

Furthermore, since we may encounter arrays of 2 dimensions or more, to access the elements within each of the arrays, we only have to specify the array we should search for. For example, for a 2-dimensional array:

array = numpy.array([[1, 2, 3], [4, 5, 6]])

print(array[0, 1])

If we do this, with array[0,1], we access the first row (As indicated by the first parameter) and then the second element of it. That is, we will obtain the number 2. If we execute:

>>> 2

Slicing

Very similar to index access, with slice we can take a set of elements from an array and use it. For example, for the following arrangement:

import numpy

arr = numpy.array([1, 2, 3, 4, 5])

print(arr[1:4])

>>> [2 3 4]

If we wanted to take the elements from a particular number to the end we only use a (number):0 as the index and the opposite if we want to start from the beginning to a certain point. Additionally, we can count negative indices starting with the last element as -1.

By adding a third parameter, we can also mention the number of elements that we jump between one point and another. With the above list:

print(arr[1:6:2])

>>> [2 4]

If we use slicing in larger arrangements, things change a little. As with the indices, we will place two parameters, only now something different will happen depending on the parameter we select.

If we have the following arrangement:

array = numpy.array([[1, 2, 3], [4, 5, 6], [7,8,9]])

And we use slicing on the first index:

print(array[1,0:2])

>>> [4 5]

We can see that in this case, we take the first and second elements of the second row, as expected. However, if we were to do the slicing on the second index:

print(array[0:3, 1])

>>> [2 5 8]

Here, we can see that we only take the first number from arrays 1 to 3 (0 to 2 depending on the order).

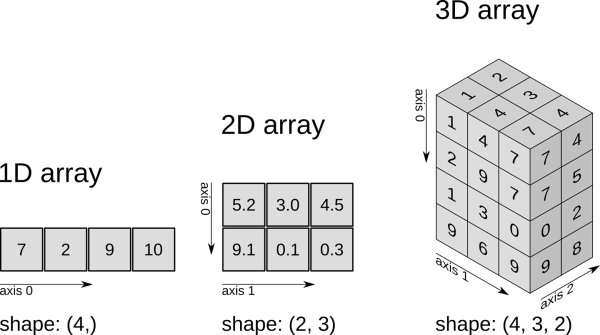
Shape

If we want to know how an array we have created is structured, we just have to use shape, a method that will return not only the number of dimensions, but the number of elements of each one. For example, if we go back to our previous example, with the arrangement:

array = numpy.array([[1, 2, 3], [4, 5, 6], [7,8,9]])

And we use arr.shape, we will have the following:

print(array.shape)

>>> (3,3)

This means that our array has two dimensions (Hence the two 3), with the first dimension, which has 3 elements (The 3 lists) and the second dimension, which also has 3 elements (The elements within the lists). .

As you can see, NumPy is a really interesting library, which will allow us to do great things with Python in the future, not just mathematical operations or creating arrays.

After reading this post, you will understand how arrays work with NumPy and how to create different types of arrays, as well as perform different operations with them. Once you master the basics, we can move on to the next stage: Handling random data and different types of functions.

Until then.

Thank you very much for your support and good luck!

math con esteroides

Shoutout to EDUCBA

En este artículo encontrarás:

• Introducción
• ¿Qué es NumPy?
• Creando Arreglos con NumPy
• Arreglos
• Algunas operaciones con arreglos en NumPy

Como programadores, al usar Python estamos trabajando constantemente con arreglos y matrices, aplicando funciones matemáticas y distintos procedimientos para obtener el resultado que queremos. Sin embargo, existe un límite con lo que podemos realizar en la versión 'vanilla' de Python.

Aún si con módulos como math podemos aumentar el rango de funciones a llevar a cabo, esto se queda corto de igual manera. Es por esto, que matemáticos y científicos que usan este lenguaje de programación para sus investigaciones suelen recurrir a una de las librerías más populares de Python: numPy.

De trabajar con matrices hasta aplicar algebra lineal y transformadas de fourier, si quieres comprobar tus cálculos y realizar cosas realmente interesantes, numPy será tu mejor opción.

Si quieres aprender que es esta librería, como usarla y su verdadero potencial, solo tienes que seguir leyendo los artículos de este nuevo arco en Coding Basics.

¡Comencemos!

¿Qué es NumPy?

Shoutout to freeCodeCamp

NumPy es una librería open source para el lenguaje Python, creada en 2005 por Travis Oliphant. Desde el principio, esta llamó la atención de la comunidad de Python, al permitir al usuario crear objetos de tipo array que respondían con una velocidad 50 veces mayor a sus consultas.

Esto es posible gracias a que los arreglos se guardan en una localización continua de la memoria, a la que el programa puede acceder facilmente.

Gracias a la contribución de su creador y gran cantidad de usuarios, ahora NumPy puede llevar a cabo gran cantidad de operaciones complejas como lo son:

• Calcular Distribución Binomial.
• Trabaja con funciones trigonométricas, logarítmicas e hiperbólicas.
• Emplear Series de Fourier.

Esto es solo un abreboca con respecto a lo que las personas logran hacer con numPy, como sistemas de reconocimiento de números escritos a mano, detectores de fraude y muchas otras cosas.

En orden de hacer el aprendizaje de numPy más ameno, en el primer artículo veremos los arreglos, parte fundamental del encanto de numPy. Estos arreglos no se ven limitados a unas pocas dimensiones como las listas y tuplas regulares en Python, sino que podemos determinar las dimensiones que queramos y realizar infinidad de operaciones sobre estos.

Dicho esto, ¿Como podemos crear arreglos con NumPy?

Creando Arreglos con numPy

Shoutout to Aprende con Alf

Antes de poder trabajar con arreglos en numPy, debemos de asegurarnos que tengamos este paquete instalado. Como siempre, si no tienes un paquete de python que deseas usar, solo tienes que instalarlo dirigiéndote a la línea de comandos, cerciorarte de que pip está instalado y entonces usar el comando:

>>> pip install [name of the library]

En este caso, ya que queremos instalar NumPy:

>>> pip install numpy

Usamos esto y esperamos unos segundos, una vez que finalice el proceso de instalación, podremos usar numpy en nuestros programas siempre que recordemos importar esta librería:

import numpy

Ahora, si queremos crear un arreglo con numpy, solo tendríamos que usar la función .array para crear un objeto de tipo ndarray, cuyo contenido podremos observar:

import numpy

array = numpy.array([1,2,3,4,5])

print(array)
print(type(array))

Si ejecutamos el programa:

>>>
[1 2 3 4 5]
<class 'numpy.ndarray'>

Otra característica realmente flexible de NumPy es que no solo tenemos que introducir listas para crear arrays, sino que también podemos usar sets y tuplas:

import numpy

array = numpy.array([1,2,3,4,5])

print(array)
print(type(array))

>>>
[1 2 3 4 5]
<class 'numpy.ndarray'>

Antes de poder realizar operaciones con arreglos, debemos tomar una clase sobre lo básico de los arreglos y las dimensiones de estos.

Arreglos

Shoutout to Indian AI Production

Como sabemos, los arreglos son una colección de datos ordenados en una sola variable, estos pueden contener un sin fin de números, strings y muchos otros datos que podemos usar a nuestro favor.

Sin embargo, hasta ahora solo hemos conocido dos tipos de arreglos, los 0-D y los 1-D. ¿Qué son estos números extraños? Bien, déjame explicarte:

Arreglos 0-D

Volviendo un poco a física, los arreglos 0-D son escalares, es decir, aquellos valores que solo tienen amplitud, magnitud o tamaño, es decir, un valor. Estos escalares son las variables que nos encontramos en el día a día con solo un valor:

x = 2

Si quisieramos crear un arreglo 0-D con numpy, solo debemos seguir el mismo procedimiento, colocando un solo valor en la función array:

import numpy

array = numpy.array(55)

print(array)
print(type(array))

>>> 55

Arreglos 1-D

Los tipos de arreglos a los que estamos acostumbrados. Un arreglo 1-D o de una dimensión es simplemente un arreglo que contiene arreglos 0-D. Estos pueden ser listas de números, sets, tuplas y muchos otros. Por ejemplo:

import numpy

array = numpy.array([55,56,57,58,59])

print(array)
print(type(array))

>>> [55 56 57 58 59]

Arreglos 2-D

A medida de que aumentamos dimensiones, nos damos cuenta de un patrón. Un arreglo de una dimensión determinada siempre va a tener dentro de si arreglos de una dimensión menor.

Esta regla sigue aplicándose a los arreglos 2-D, los cuales son arreglos que contienen arreglos 1-D como sus elementos. Tambien se pueden usar para representar matrices ya que siguen una estructura similar a la columna/fila usada por estas, con arreglos anidados. Observándolo:

import numpy

arr = numpy.array([[3, 3, 3], [3, 3, 3]])

print(arr)

>>>
[[3 3 3]
 [3 3 3]]

Arreglos 3-D

Siguiendo la tradición, los arreglos 3-D tienen arreglos 2-D como sus elementos:

import numpy

arr = numpy.array([[[3, 3, 3], [3, 3, 3]],[[3, 3, 3], [3, 3, 3]]])

print(arr)

>>>
[[[3 3 3]
  [3 3 3]]

 [[3 3 3]
  [3 3 3]]]

Esto seguirá para cada dimensión, donde si queremos chequear la dimensión de un arreglo solo debemos de usar el método ndim:

print(array.ndim())
>>> 3 

Si queremos crear arreglos de mayores dimensiones (4,5,6,etc...), podemos hacerlo manualmente, un proceso realmente tedioso, o asignar la cantidad de dimensiones por medio de otro parámetro, conocido como ndmin o número de dimensiones. Si por ejemplo, quisieramos crear un arreglo de 8 dimensiones, hacemos lo siguiente:

import numpy

arr = numpy.array([[[3, 3, 3], [3, 3, 3]],[[3, 3, 3], [3, 3, 3]]], ndmin=8)

print(arr)

>>>
[[[[[[[[3 3 3]
       [3 3 3]]

      [[3 3 3]
       [3 3 3]]]]]]]]

Algunas operaciones con arreglos en NumPy

Shoutout to Towards Data Science

Al igual que los arreglos propios de Python como listas, sets y tuplas, podemos realizar una serie de operaciones sobre los arreglos creados con numpy. Entre estas tenemos:

Indexing (Acceso a Índice)

Una operación muy común en arreglos donde el orden de los elementos importa. Si queremos acceder a uno de los elementos de una lista que creemos, solo basta con colocar la lista y entre brackets el número del índice donde se encuentra el elemento:

list[index]

Esto será exactamente lo que haremos con los arreglos creados por numpy, donde solo colocamos el número del elemento y accedemos a el. Ejemplo:

import numpy

array = numpy.array([1,2,3,4,5])

print(array[0])

>>> 1

Además, ya que podemos llegar a encontrarnos con arreglos de 2 dimensiones o más, para acceder a los elementos dentro de cada uno de los arreglos, solo debemos especificar el arreglo que debemos buscar. Por ejemplo, para un arreglo de 2 dimensiones:

array = numpy.array([[1, 2, 3], [4, 5, 6]])

print(array[0, 1])

Si realizamos esto, con array[0,1], accedemos a la primera fila (Como nos lo indica el primer parámetro) y luego al segundo elemento de esta. Es decir, obtendremos el número 2. Si ejecutamos:

>>> 2

Slicing

Muy similar al acceso por índice, con slice podremos tomar un conjunto de elementos de un arreglo y usarlo. Por ejemplo, para el siguiente arreglo:

import numpy

arr = numpy.array([1, 2, 3, 4, 5])

print(arr[1:4])

>>> [2 3 4]

Si quisieramos tomar los elementos desde un número particular hasta el final solo usamos como índice a (número):0 y lo opuesto si queremos empezar desde el inicio hasta cierto punto. Además, podemos contar con índices negativos empezando por el último elemento como -1.

Agregando un tercer parámetro, también podemos mencionar la cantidad de elementos que saltamos entre un punto y otro. Con la lista anterior:

print(arr[1:6:2])

>>> [2 4]

Si usamos slicing en arreglos de mayores dimensiones, la cosa cambia un poco. Al igual que con los índices, colocaremos dos parámetros, solo que ahora de acuerdo al parámetro que seleccionemos pasará algo distinto.

Si tenemos el siguiente arreglo:

array = numpy.array([[1, 2, 3], [4, 5, 6], [7,8,9]])

Y usamos slicing en el primer índice:

print(array[1,0:2])

>>> [4 5]

Podemos ver que en este caso, tomamos el primer y segundo elemento de la segunda fila, como es esperado. Sin embargo, si hicieramos el slicing en el segundo índice:

print(array[0:3, 1])

>>> [2 5 8]

Aquí, podemos observar que solo tomamos el primer número de los arreglos 1 a 3 (0 a 2 según el orden).

Shape

Si queremos saber como está estructurado un arreglo que hayamos creado, solo tenemos que usar shape, un método que nos devolverá no solo el número de dimensiones, sino la cantidad de elementos de cada uno. Por ejemplo, si volvemos a nuestro ejemplo previo, con el arreglo:

array = numpy.array([[1, 2, 3], [4, 5, 6], [7,8,9]])

Y usamos arr.shape, tendremos lo siguiente:

print(array.shape)

>>> (3,3)

Esto nos quiere decir que nuestro arreglo tiene dos dimensiones (Por eso los dos 3), con la primera dimensión, que tiene 3 elementos (Las 3 listas) y la segunda dimensión, que tiene 3 elementos también (Los elementos dentro de las listas).

Como podrás ver, NumPy es una librería realmente interesante, que nos permitirá en un futuro realizar grandes cosas con Python, no solo operaciones matemáticas o crear arreglos.

Tras leer este post, entenderás como funcionan los arreglos con NumPy y como crear distintos tipos de arreglos, así como realizar distintas operaciones con estos. Una vez que domines lo básico, podremos pasar a la siguiente etapa: El manejo de datos aleatorios y distintos tipos de funciones.

Hasta ese entonces.

¡Muchas gracias por tu apoyo y buena suerte!