More than just adding and substracting

Shoutout to Real Python

In this article you'll find:

• Introduction
• What is the math Module?
• Some methods of math
• A small example

Finally, before tackling more complex topics such as regular expressions, exception handling and the handling of GUI modules such as tkinter as well as downloadable libraries with pip install, we will take a look at math, a module that allows us to extend the amount of mathematical operations that we can implement in our development environment.

From square roots and rounding to finding the sine and cosine of a function, math will give us everything we need to have an efficient Matlab replacement (to some extent).

That said, if you want to learn how to make your first years of college easier through programming, just keep reading.

Let's get started!

What is the Math module?

Shoutout to Electroica Blog

By default, programming languages such as Python come with mathematical functions included, for which there is no need to invoke any module. For example, we have:

• min, which returns the minimum between the parameters entered. Ex:

min_num = min(2,7,20)
print(min_num)
>>> 2

• pow, which returns the power of the first parameter raised to the second parameter:

pow_som = pow(2,6)
print(pow_som)
>>> 64

However, there comes a point where these default functions fall short. What if we want to determine the square root of a number? What if I want to calculate the factorial of any number?

This is where math comes in, a module that allows us to add the math class, which will have a large number of methods and constants that will help us solve complex mathematical problems. The only thing to do is to resort to the import:

import math

And thus, if we want to calculate the square root of 24:

print(math.sqrt(24))
>>> 4.8989794855663561963945681494118

Some methods of math:

Shoutout to IPCisco

math.degrees and math.radians

If you are an engineering student or are watching physics, you will know how tedious it is to have to constantly switch between radians and degrees. With math.degrees and math.radians you won't have this problem again.

All you have to do is enter the degrees or radians you want to convert as a parameter and you will get a result:

print(math.degrees(90))
print(radians(90))
>>>
5156.620156177409
1.5707963267948966 ## Which is pi/2

math.floor and math.ceil

There will be certain cases where you want to round a number to a smaller or larger value, but you don't want to create super complex logic to do so. In order to solve this, you just use the floor and ceil methods.

floor, as the name implies, is used to round a number down (The floor), while ceil rounds it up to the next number (The ceiling). So, if we have 8.5:

print(math.floor(8.5))
print(math.ceil(8.5))

>>>
8
9

sin, cos and tan

If you want to calculate trigonometric identities for a particular angle, just use math.sin, cos or tan and the rest of the arctangent methods. Trying for the sine, cosine and tangent value of pi:

print(math.sin(3.1415926535897932384626433832795))
print(math.cos(3.1415926535897932384626433832795))
print(math.tan(3.1415926535897932384626433832795))

>>>
-0.4480736161291701
0.8939966636005579
-1.995200412208242

Note, if we want to use pi and we don't want to write a bunch of numbers, we just use the pi constant, built into math. Thus:

print(math.pi)
>>> 3.141592653589793

Likewise, for T=2*pi, we use math.tau

A small example:

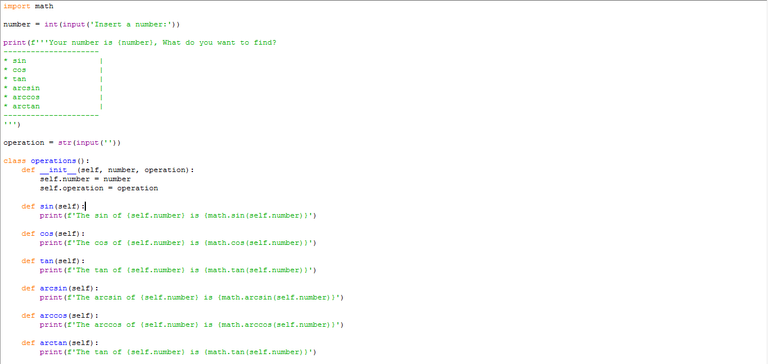
In this case we will create a trigonometric identity calculator. To begin, we must create a variable that asks us for a number. We will do this with the input function, which will cause a line of text to allow us to enter values to the variable.

In the same way we will use int, to stipulate that the value must be an integer:

number = int(input('Insert a number:'))

Next, we will show the user the number he chose and give him to select from the available trigonometric identities. Like this:

print(f'''Your number is {number}, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------
''')

Note: To make it easier to place variable values inside a string, we make use of the fstring, which allows us to place the value of the variable in our text just by identifying it inside square brackets {}

First, we must request the operation to select in text, reason for which we place a variable called operation that will be an input, where we will use str to corroborate that it is a string.

operation = str(input(''))

Now, we will identify that, in case a specific option is selected, a function will be executed. For the part of evaluating specific conditions, we will use the match case conditionals, while in order to keep everything organized, we create the functions for each operation in the form of methods of a single class, called operations:

So, if we first create the class and the methods:

class operations():
     def __init__(self, number, operation):
          self.number = number
          self.operation = operation

    def sin(self):
        print(f'The sin of {self.number} is {math.sin(self.number)}')

    def cos(self):
        print(f'The cos of {self.number} is {math.cos(self.number)}')

    def tan(self):
        print(f'The tan of {self.number} is {math.tan(self.number)}')

    def arcsin(self):
        print(f'The arcsin of {self.number} is {math.arcsin(self.number)}')

    def arccos(self):
       print(f'The arccos of {self.number} is {math.arccos(self.number)}')

    def arctan(self):
      print(f'The tan of {self.number} is {math.tan(self.number)}')

Note: Create the class before the match case conditionals. Otherwise, it will tell us that the class does not exist.

In the constructor of the class we identify two attributes (the parameters), which will be the number at which we will execute the selected trigonometric identity and the other, corresponding to the operation.

Then, we only define the methods with fstrings (Comment if you want a chapter of Coding Basics dedicated to fstrings) and with math we do the rest.

Now, for the conditionals, it only remains to create an object that contains the number and the operation as parameters:

obj1 = operations(number,operation)

And finally, execute the match case:

match obj1.operation:
    case 'sin':
          obj1.sin()
    case 'cos':
          obj1.cos()
    case 'tan':
          obj1.tan()
    case 'arcsin':
         obj1.arcsin()
    case 'arccos':
         obj1.arccos()
    case 'arctan':
        obj1.arctan()
    case _:
        print('Invalid Operation')

In its entirety, the code would look as follows:

import math

number = int(input('Insert a number:'))

print(f'''Your number is {number}, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------
''')

operation = str(input(''))

class operations():
    def __init__(self, number, operation):
        self.number = number
        self.operation = operation

    def sin(self):
        print(f'The sin of {self.number} is {math.sin(self.number)}')

    def cos(self):
        print(f'The cos of {self.number} is {math.cos(self.number)}')

    def tan(self):
        print(f'The tan of {self.number} is {math.tan(self.number)}')

    def arcsin(self):
        print(f'The arcsin of {self.number} is {math.arcsin(self.number)}')

    def arccos(self):
        print(f'The arccos of {self.number} is {math.arccos(self.number)}')

    def arctan(self):
        print(f'The tan of {self.number} is {math.tan(self.number)}')

obj1 = operations(number,operation)

match obj1.operation:
    case 'sin':
        obj1.sin()
    case 'cos':
        obj1.cos()
    case 'tan':
        obj1.tan()
    case 'arcsin':
        obj1.arcsin()
    case 'arccos':
        obj1.arccos()
    case 'arctan':
        obj1.arctan()
    case _:
        print('Invalid Operation')    

And when executing, taking as an example the 5 and choosing tan, we will have:

>>>
Insert a number:5
Your number is 5, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------

tan
The tan of 5 is -3.380515006246586

The math module is an excellent help for those programmers who want to make use of mathematical operations to reach concrete results such as obtaining accurate graphs and extracting relevant information about them.

That is why, after this, you will not only understand more deeply how the modules work, but you will open another world of probabilities. I invite you to investigate more about the math module and put your knowledge into practice.

Thanks for your support and good luck!

Más que solo sumar y restar

Shoutout to Real Python

En este artículo encontrarás

• Introducción
• ¿Qué es el módulo math?
• Algunos métodos de math
• Un pequeño ejemplo

Finalmente, antes de atacar temas más complejos como lo son las expresiones regulares, el exception handling y el manejo de módulos de interfaces gráficas como tkinter así como librerías descargables con pip install, daremos un vistazo a math, un módulo que nos permite extender la cantidad de operaciones matemáticas que podemos implementar en nuestro entorno de desarrollo.

Desde raíces cuadradas y redondeo hasta buscar el seno y coseno de una función, math nos brindará todo lo que necesitamos para tener un reemplazo eficiente de Matlab (Hasta cierto punto).

Dicho esto, si quieres aprender como hacer que tus primeros años universitarios sean más sencillos por medio de programación, solo tienes que seguir leyendo.

¡Comencemos!

¿Qué es el módulo Math?

Shoutout to Electroica Blog

Por defecto, lenguajes de programación como Python traen funciones matemáticas incluidas, para las cuales no hace falta invocar módulo alguno. Por ejemplo, tenemos:

• min, que nos retorna el mínimo entre los parámetros

introducidos. Ej:

min_num = min(2,7,20)
print(min_num)
>>> 2

• pow, que nos retorna la potencia del primer parámetro elevado al segundo parámetro:

pow_som = pow(2,6)
print(pow_som)
>>> 64

Sin embargo, llega un punto en el cual estas funciones por defecto se quedan cortas. ¿Qué pasaría si quisieramos determinar la raíz cuadrada de un número? ¿Que pasa si quiero calcular el factorial de cualquier número?

Aquí, es donde se hace presente math, un módulo que nos permite agregar la clase math, que tendrá una gran cantidad de métodos y constantes que nos ayudarán a solucionar problemas matemáticos complejos. Lo único que hay que hacer es recurrir al import:

import math

Y así, si queremos calcular la raíz cuadrada de 24:

print(math.sqrt(24))
>>> 4.8989794855663561963945681494118

Algunos métodos de math

Shoutout to IPCisco

math.degrees y math.radians

Si eres un estudiante de ingeniería o estás viendo física, sabrás que tan tedioso es tener que cambiar constantemente entre radianes y grados. Con math.degrees y math.radians no tendrás este problema de nuevo.

Lo único que tienes que hacer es introducir como parámetro los grados o radianes que quieres convertir y tendrás un resultado:

print(math.degrees(90))
print(radians(90))
>>> 
5156.620156177409
1.5707963267948966 ## Which is pi/2

math.floor y math.ceil

Habrán ciertos casos donde quieras redondear un número a un valor menor o mayor, pero no quieres crear lógica super compleja para hacerlo. En orden de solucionar esto, solo debes usar los métodos floor y ceil.

floor, como su nombre lo indica, es usado para redondear un número hacia abajo (El suelo), mientras que ceil lo redondea al siguiente número (El techo). Así, si tenemos 8.5:

print(math.floor(8.5))
print(math.ceil(8.5))

>>> 
8
9

sin, cos and tan

Si quieres calcular identidades trigonométricas para un ángulo en particular, solo debes usar math.sin, cos o tan y el resto de métodos arcotangentes. Probando para el seno, coseno y tangente del valor de pi:

print(math.sin(3.1415926535897932384626433832795))
print(math.cos(3.1415926535897932384626433832795))
print(math.tan(3.1415926535897932384626433832795))

>>> 
-0.4480736161291701
0.8939966636005579
-1.995200412208242

Nota, si queremos usar pi y no queremos escribir un montón de números, solo debemos usar la constante pi, incorporada en math. Así:

print(math.pi)
>>> 3.141592653589793

De igual manera, para T=2*pi, usamos math.tau

Un pequeño ejemplo

En este caso crearemos una calculadora de identidades trigonométricas. Para empezar, debemos crear una variable que nos pida un número. Esto lo haremos con la función input, que hará que una línea de texto nos permita introducir valores a la variable.

De igual manera usaremos int, para estipular que el valor debe ser entero:

number = int(input('Insert a number:'))

Después, le mostraremos al usuario el número que escogió y le daremos a seleccionar entre las identidades trigonométricas disponibles. Así:

print(f'''Your number is {number}, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------
''')

Nota: Para hacer más sencillo el colocar valores de variable dentro de una string, hacemos uso de las fstring, que nos permiten colocar el valor de la variable en nuestro texto con solo identificarlo dentro de corchetes ({}).

Primero, debemos de solicitar la operación a seleccionar en texto, razón por la que colocamos una variable llamada operation que será un input, donde usaremos str para corroborar que sea una string.

operation = str(input(''))

Ahora, nos tocará identificar que, en caso de que se seleccione una opción específica, se ejecute una función. Para la parte de evaluar condiciones específicas, usaremos los condicionales match case, mientras que en orden de mantener todo organizado, creamos las funciones para cada operación en forma de métodos de una sola clase, llamada operaciones:

Así, si primero creamos la clase y los métodos:

class operations():
    def __init__(self, number, operation):
        self.number = number
        self.operation = operation

    def sin(self):
        print(f'The sin of {self.number} is {math.sin

(self.number)}')

    def cos(self):
        print(f'The cos of {self.number} is {math.cos

(self.number)}')

    def tan(self):
        print(f'The tan of {self.number} is {math.tan

(self.number)}')

    def arcsin(self):
        print(f'The arcsin of {self.number} is {math.arcsin

(self.number)}')

    def arccos(self):
        print(f'The arccos of {self.number} is {math.arccos

(self.number)}')

    def arctan(self):
        print(f'The tan of {self.number} is {math.tan

(self.number)}')

Nota: Crear la clase antes de los condicionales match case. En
caso contrario, nos dirá que no existe la clase.

En el constructor de la clase identificamos dos atributos (Los parámetros), que serán el número al que ejecutaremos la identidad trigonométrica seleccionada y el otro, correspondiente a la operación.

Luego, solo definimos los métodos con fstrings (Comenta si quieres un capítulo de Coding Basics dedicado a las fstrings) y con math hacemos el resto.

Ahora, para los condicionales, solo queda crear un objeto que contenga al número y la operación como parámetros:

obj1 = operations(number,operation)

Y finalmente, ejecutar el match case:

match obj1.operation:
    case 'sin':
        obj1.sin()
    case 'cos':
        obj1.cos()
    case 'tan':
        obj1.tan()
    case 'arcsin':
        obj1.arcsin()
    case 'arccos':
        obj1.arccos()
    case 'arctan':
        obj1.arctan()
    case _:
        print('Invalid Operation')

En su totalidad, el código se vería de la siguiente manera:

import math

number = int(input('Insert a number:'))

print(f'''Your number is {number}, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------
''')

operation = str(input(''))

class operations():
    def __init__(self, number, operation):
        self.number = number
        self.operation = operation

    def sin(self):
        print(f'The sin of {self.number} is {math.sin

(self.number)}')

    def cos(self):
        print(f'The cos of {self.number} is {math.cos

(self.number)}')

    def tan(self):
        print(f'The tan of {self.number} is {math.tan

(self.number)}')

    def arcsin(self):
        print(f'The arcsin of {self.number} is {math.arcsin

(self.number)}')

    def arccos(self):
        print(f'The arccos of {self.number} is {math.arccos

(self.number)}')

    def arctan(self):
        print(f'The tan of {self.number} is {math.tan

(self.number)}')

obj1 = operations(number,operation)

match obj1.operation:
    case 'sin':
        obj1.sin()
    case 'cos':
        obj1.cos()
    case 'tan':
        obj1.tan()
    case 'arcsin':
        obj1.arcsin()
    case 'arccos':
        obj1.arccos()
    case 'arctan':
        obj1.arctan()
    case _:
        print('Invalid Operation')      

Y al ejecutar, tomando como ejemplo el 5 y escogiendo a tan, tendremos:

>>>
Insert a number:5
Your number is 5, What do you want to find?
---------------------
* sin                |
* cos                |
* tan                |
* arcsin             |
* arccos             |
* arctan             |
---------------------

tan
The tan of 5 is -3.380515006246586

El módulo math es una excelente ayuda para aquellos programadores que quieran hacer uso de operaciones matemáticas para llegar a resultados concretos como la obtención de gráficas precisas y extraer informacion relevante sobre estas.

Es por esto, que después de esto, no solo entenderás más a profundidad como funcionan los módulos, sino que abrirás otro mundo de probabilidades. Te invito a investigar más sobre el módulo math y a poner tus conocimientos en práctica.

¡Gracias por tu apoyo y buena suerte!