Secuencias de Pascal / Pascal's sequences [ ES / EN ]
| Español | English |
Supongamos una secuencia d,
a partir de ésta generemos otra secuencia s,
mediante la aplicación de las reglas siguientes,
s0 = d0
sk = dk - 1 + dk ( 1 ≤ k ≤ n)
sn + 1 = dn
Llamamos Ley de Pascal a las reglas que hemos definido para derivar una secuencia de otra, las distintas secuencias que podemos obtener aplicando de forma reiterada estas reglas se conocen como Secuencias de Pascal.
Si aplicamos la Ley de Pascal de forma reiterada a la secuencia,
obtenemos la Secuencia de Pascal que genera el Triángulo de Pascal.
| 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
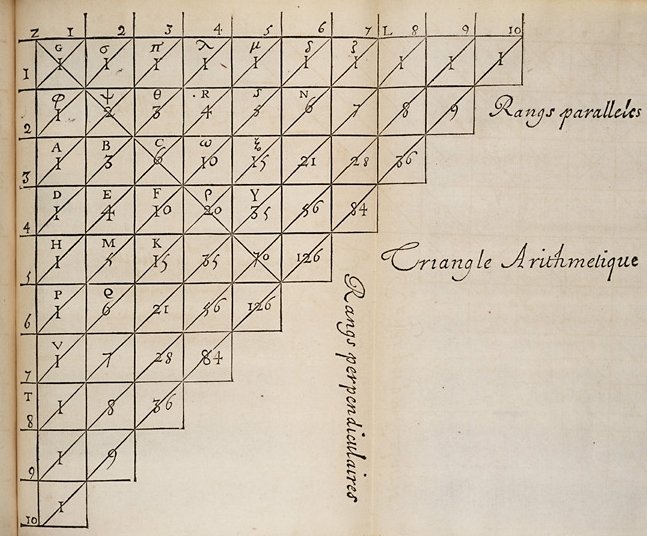
Si disponemos las secuencias, la una debajo de la otra, de forma que cada número de cada secuencia se encuentra debajo y entre los números de la secuencia precedente que sumados lo generan, obtenemos la representación de la Secuencia de Pascal más popular.
Para construir el Triángulo de Pascal no son necesarias las Secuencias de Pascal, podemos considerar el Triángulo de Pascal como una tabla numérica infinita con la primera fila y la primera columna a todo 1 y con el resto de entradas igual a la suma de los valores a su izquierda y por encima.
1 |
1 |
1 |
1 |
1 |
1 |
|---|---|---|---|---|---|
1 |
2 |
3 |
4 |
5 |
|
1 |
3 |
6 |
10 |
||
1 |
4 |
10 |
|||
1 |
5 |
||||
1 |
| English | Español |
Consider a sequence d,
derive a new sequence s from d,
by de following rule,
s0 = d0
sk = dk - 1 + dk ( 1 ≤ k ≤ n)
sn + 1 = dn
We say that this new sequence is derived from the original one by Pascal's Relations.
Applying the Pascal's Relations to the sequence,
a sequence arises that we know as the Pascal's Triangle.
| 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
Write down Pascal's sequences, one under another, so that each number of each sequence is found between and below those numbers from which it is calculated. We obtain the Pascal's Triangle.
Others methods could be given to construct the Pascal's Triangle without relying on the notions of Pascal's Relations or Pascal's Sequences. Pascal’s Triangle is simply an infinite numerical table in which each entry along the sides is 1, and in which each of the other entries is the sum of the two entries above it, to the right and to the left.
1 |
1 |
1 |
1 |
1 |
1 |
|---|---|---|---|---|---|
1 |
2 |
3 |
4 |
5 |
|
1 |
3 |
6 |
10 |
||
1 |
4 |
10 |
|||
1 |
5 |
||||
1 |
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @j2e2xae! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 300 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: