Superposición e interferencia de ondas
¡Hola querida comunidad científica de Hive! reciban todos un cordial saludo, el día de hoy finalizaremos nuestro hermoso paseo por el mundo de las ondas, hablaremos un poco sobre la superposición e interferencia de ondas.
Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva
Cuando dos o más ondas se desplazan a través de un medio, la onda resultante, en cualquier punto de su travesía, es la suma algebraica de las ondas individuales. Lo establecido anteriormente, constituye el principio de superposición aplicado a las ondas. Es importante resaltar que de este principio derivan dos consecuencias importantes:
1- Dos ondas pueden pasar por el mismo sitio, interferir una con la otra y salir del punto de encuentro, sin sufrir alteraciones.
2- Cuando dos ondas se encuentran producen un patrón de onda que difiere e cada una de ellas individualmente.
La interferencia de ondas denota lo que sucede cuando dos o más ondas se cruzan en la misma región del espacio. Cuando dos ondas interfieren, se observa el efecto neto de esta interacción, que se puede visualizar usando el principio de superposición. Patrones típicos de interferencia los encontramos en la propagación de pulsos de ondas, creados en los dos extremos de una cuerda, y que se acercan entre sí. Si observamos con detenimiento la imagen que se presenta a continuación veremos dos picos e onda que viajan en sentidos contrarios y tienen como punto de encuentro la recta N. Cuando los dos picos se cruzan en la recta N, sus valores se suman punto a punto, dando origen a la onda de color marrón mostrada en las partes B, C y D de la imagen mencionada. Cuando las dos ondas coinciden como en la parte c, sus picos se suman en el centro de la recta N se alcanza el valor máximo, producto de la interferencia de las ondas. Luego de cruzarse, cada onda se aleja de la recta N sin sufrir una alteración notable.
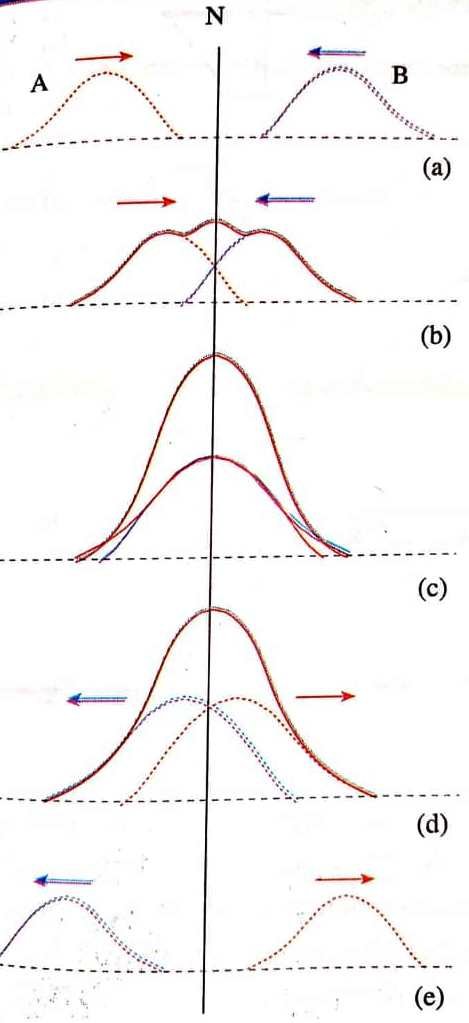
Fuente: Figuera (2009)
Al tipo de interferencia descrito anteriormente se le conoce como interferencia constructiva, porque los efectos de las ondas se refuerzan al encontrarse. Esta interferencia tiene lugar cuando dos picos o dos valles de ondas se encuentran. El medio por donde viajan las ondas experimenta un desplazamiento, en el caso de ondas mecánicas, como resultado de la interacción aditiva de las perturbaciones del medio.
Se produce interferencia destructiva cuando un pico y un valle de dos ondas se encuentran. La onda resultante corresponde a la línea de color marrón que podemos ver en la imagen posterior. Cuando el pico de una onda y el valle de la otra se colocan simétricamente alrededor de la línea N, los efectos de las perturbaciones se cancelan, por lo que no se observa ninguna onda. Esto es representado por la línea marrón, coincidente con el eje horizontal, tal como lo podemos en la parte C de la imagen. En todo momento, el resultado corresponde a la diferencia, punto a puno, de las dos ondas. Luego de producirse la interferencia, cada onda sigue su propagación en forma independiente.
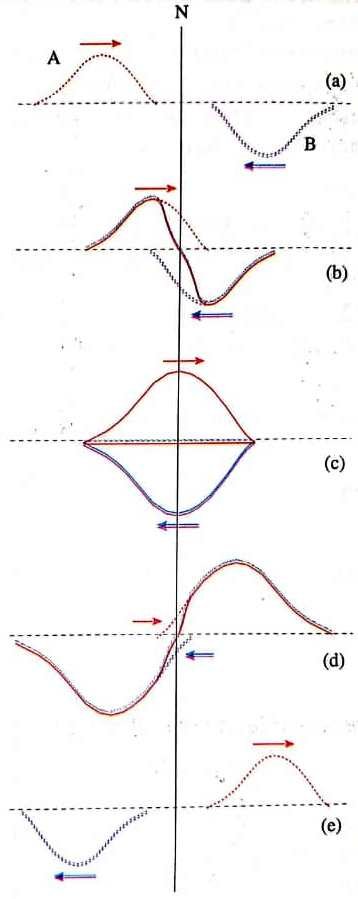
Fuente: Figuera (2009)
Los patrones de interferencia pueden resultar muy complejos, dependiendo de las características de las ondas envueltas en la interacción.
Cuando una onda viaja en un medio, se propaga en forma indefinida, a menos que encuentre un obstáculo que modifique su propagación. A esta onda que se transmite en un medio sin relajarse, se le llama onda viajera. Las ondas oceánicas son ejemplos de ondas viajeras. Son notables, dentro de ellas, las perturbaciones oceánicas generadas por los maremotos, que se propagan por miles de kilómetros, antes de alcanzar la playa.
Cuando una onda consigue un obstáculo, parte de la misma se refracta y pate se refleja. La onda reflejada interfiere con cualquier otra onda incidente, para generar un patrón que puede parecerse o no a la perturbación original.
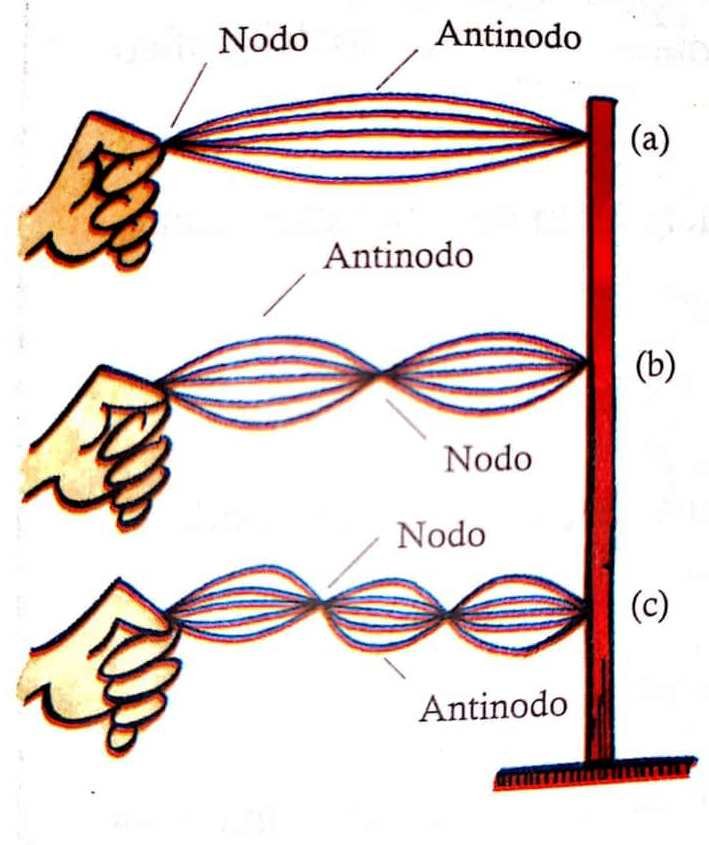
Fuente: Figuera (2009)
Como en ocasiones anteriores, consideremos una cuerda, uno de cuyos extremos se encuentra fijo, mientras que el otro extremo se somete a un movimiento vertical periódico, que genera una onda sinusoidal permanente. Si se hace oscilar la cuerda a la frecuencia adecuada, las ondas incidentes y reflejadas pueden interferir, produciendo un efecto de onda estacionaria en la cuerda, lo cual da la sensación de que no se mueve onda alguna a lo largo de la misma. A los puntos de mayor amplitud sobre la cuerda se les conoce con el nombre de antinodos y a los de menor amplitud, se les llama nodos.
La frecuencia de oscilación más baja corresponde a la parte A de la imagen anterior, mientras que en la B y C la cuerda oscila a frecuencia doble y triple e la frecuencia más baja.
Las frecuencias a las cuales se originan ondas estacionarias se conocen como frecuencias de resonancia. A la primera frecuencia e resonancia se le llama frecuencia fundamental o primer armónico; a la segunda, segundo armónico y así sucesivamente.
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen I. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1401330625911656450?s=20
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.