More worked examples of Sequence and Series

In the last lesson, we saw what a sequence is and how to find the nth term of a sequence. We also solved some given examples of a set of numbers in a sequence. Then we understood what a series is and how to find the series of a sequence. Now we will try to solve some examples in order to understand the subject more.
Example 1
Find the first five terms of a sequence whose nth term is given below:
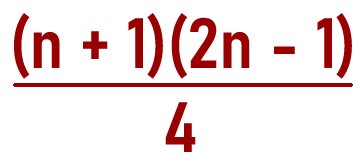
Solution:
Given the nth term as (n + 1)(2n - 1)/4
Substituting n = 1 in the nth term, we have
T1 = (1 + 1)(2x1 - 1)/4
T1 = (1 + 1)(2 - 1)/4
T1 = (1 + 1)(2 - 1)/4
Expanding the bracket, we have:
T1 = 2x1/4
T1 = 2/4
Dividing to the lowest term, we have
T1 = 1/2
Substituting n = 2 in the nth term, we have
T2 = (2 + 1)(2x2 - 1)/4
T2 = (2 + 1)(4 - 1)/4
T2 = (3)(3)/4
Expanding the bracket, we have:
T2 = 9/4
Substituting n = 3 in the nth term, we have
T3 = (3 + 1)(2x3 - 1)/4
T3 = (3 + 1)(6 - 1)/4
T3 = (4)(5)/4
Expanding the bracket, we have:
T3 = 20/4
T3 = 5
Substituting n = 4 in the nth term, we have
T4 = (4 + 1)(2x4 - 1)/4
T4 = (4 + 1)(8 - 1)/4
T4 = (5)(7)/4
Expanding the bracket, we have:
T4 = 35/4
Substituting n = 5 in the nth term, we have
T5 = (5 + 1)(2x5 - 1)/4
T5 = (5 + 1)(10 - 1)/4
T5 = (6)(9)/4
Expanding the bracket, we have:
T5 = 54/4
Dividing to the lowest term, we have
T5 = 27/2
Therefore, the first 5 terms are: 1/2, 9/4, 5, 35/4, 27/2
Example 2
Find the sum of the second and third terms of a sequence whose nth term is denoted by:
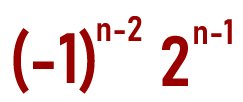
Solution
Given the nth term as (-1)n-2 2n-1
Substituting n = 2 in the nth term, we have
T2 = (-1)2-2 22-1
T2 = (-1)0 21
Remember in law of indices that any number raised to the power of zero is 1. We then have:
T2 = 1 x 2
T2 = 2
Substituting n = 3 in the nth term, we have
T3 = (-1)2-3 23-1
T3 = (-1)-1 22
Expanding the bracket, we have
T3 = -1 x 4
T3 = -4
The sum of the 2nd and 3rd terms is:
T2 + T3 = 2 + (-4)
T2 + T3 = 2 - 4
T2 + T3 = -2
Example 3
What is the sum of the first 6 terms of the sequence below:

Solution
Given the nth term as 3n - 2
Substituting n = 1 in the nth term, we have
T1 = (3x1 - 2)
T1 = (3 - 2)
T1 = 1
Substituting n = 2 in the nth term, we have
T2 = (3x2 - 2)
T2 = (6 - 2)
T2 = 4
Substituting n = 3 in the nth term, we have
T3 = (3x3 - 2)
T3 = (9 - 2)
T3 = 7
Substituting n = 4 in the nth term, we have
T4 = (3x4 - 2)
T4 = (12 - 2)
T4 = 10
Substituting n = 5 in the nth term, we have
T5 = (3x5 - 2)
T5 = (15 - 2)
T5 = 13
Substituting n = 6 in the nth term, we have
T6 = (3x6 - 2)
T6 = (18 - 2)
T6 = 16
Therefore, the sum of the first 6 terms will be:
T1 + T2 + T3 + T4 +T5 + T6 = 1+4+7+10+13+16 = 51
Conclusion
I believe with the example, the subject is now clearer and easier to understand. Once you have the nth term of the sequence, it will be possible to solve for the unknown positions in the sequence. Even if the nth term is unknown, the figures of the sequence will be used to determine the nth term.
Congratulations @fokusnow! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 3750 replies.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.