Looking at more solved examples of Joint variation

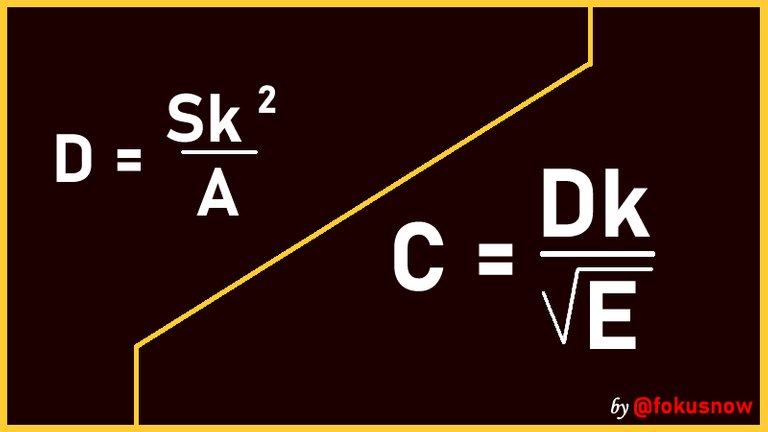
Yesterday, I introduced joint variation and we were able to see a few examples of real life application of joint variation. We also saw some worked examples too. Basically, it was understood that a joint variation has to do with a quantity that changes value based on the value of two other variables. That is really the idea of naming it joint variation. To understand it further, we will look at some more solved examples of joint variation. Of course it is not something new. We will still follow the methods that was introduced in the previous presentation. Lets get into it proper.

Example 1

A truck travels on a highway such that the distance travelled by the car is directly proportional to the square of its speed and inversely proportional to its acceleration. If the distance travelled is 8m and the speed is 6km/h and the acceleration is 9km/h, find the following:

(i) the distance travelled if the speed is 3km/h and acceleration is 2km/h
(ii) the speed if it travelled a distance of 24m with an acceleration of 6km/h
Solution

(First step: We need to find the relationship between the quantities, and find the value of the constant.)

Let Distance D = 8
Speed S = 6
Acceleration A = 9

D ∝ S²/A
(Next step: Introducing the constant k)
D = S²k/A
(Use the initial values to solve for k)
8 = 6²k/9
8 = 36k/9
(Next step: Cross multiply to make k the subject)
36k = 8 x 9
36k = 72
k = 72/36
k = 2

Now lets solve for the unknowns
(i) the distance travelled if the speed is 3km/h and acceleration is 2km/h

D = S²k/A
D = 3²x2/2
D = 9 x 2/2
D =18/2
S = 9

(ii) the speed if it travelled a distance of 8m with an acceleration of 2km/h
D = S²k/A
24 = S²x2/2
(Cross multiply to make S the subject)
2S² = 25x2
2S² = 50
S² = 50/2
S² = 25
(Introduce square root on the right hand side to cancel the square)
S = √25
S = 5
(Collect like terms such that 2 turns to division as it crosses equality sign)

Example 2

If C varies directly as D and inversely as the square root of E. C = 300, when D = 65, E = 25. Solve for the value of C when D = 468 and E = 144.

Solution

(First step: We need to find the relationship between the quantities, and find the value of the constant.)

C ∝ D/√E
(Next step: Introducing the constant k)
C = Dk/√E
(Use the initial values to solve for k)
300 = 65k/√25
(Cross-multiply to make k the subject)
65k = 300x5
65k = 1500
(Collecting like terms and making 65 divide the other side of the equation, we have)
k = 1500/65
k = 23.07

Finding C when D = 468 and E = 144.
C = Dk/√E
C = 468x23/√144
C = 10764/7
C = 1537.7

Conclusion

We have seen examples of joint variation and how to solve them. Its really not too difficult at all if you find your constant and substitute other variables. In our next presentation, we will be looking at the other forms of variation and methods of solving the arithmetic involved.