Change of subject of formula - some complex examples

over 1 year ago

I introduced this important arithmetic yesterday and we were able to see what change of subject is and how to make any quantity in an equation subject of the formula. We were able to see few not so hard examples of how to make any variable the subject. In todays presentation, we are going to work with a little bit harder examples of changing the subject of any formula or equation.

So going straight into examples, lets look at the following 2:

Example 1: Make n the subject of the formula below:

Solution:
(first step: The first thing to do is to remove the square root sign on the right side of the equation by introducing square on the left side. As such, we will have:)

x = √n+v/v (1 + vn)
x² = n+v/v (1 + vn)

(next step: We have to expand the denominator of the fraction on the right side of the equals sign. Thus:)

x² = n+v/(v + v²n)

(next step: We need to cross-multiply the variables on the left with the ones on the right since they are fractions. We then have:)

x² (v + v²n) = n+v

(next step: We have to expand the bracket on our left side by multiplying all the variables in the bracket by x², that will give us:)

x² v + v² n x² = n+v

(next step: We have to collect like terms and place them each on either sie of the equals sign. Thus, we will have:)

v² n x² - n = v - x² v

(next step: We can factorize each side of the equation to make n the subject as follows:)

n(v² x² - 1) = v (1 - x²)

(next step: Finally isolating n which is the subject, we will move the rest of the expression on the left to the right. Remember, when multiplication crosses the equals sign, it turns to division. Therefore:)

n = v (1 - x²)/(v² x² - 1)

So the final equation below shows we have made n the subject:

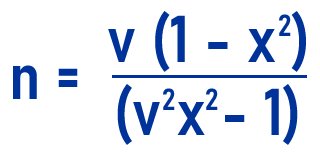
Example 2: Make f the subject of the formula in the expression below:

Solution:

S = ut + 1/2ft²

(first step: Convert the last set of variables at the right hand side of the equals sign to a faction. We will have:)

S = ut + ft²/2

(next step: Collect like terms, i.e the variables that are not in fraction form and the ones that are in fraction form. When ut crosses the equals sign, it turns to negative. We will have:)

S - ut = ft²/2

(next step: We will cross multiply the expression on the left side with the one on the right side. That gives:)

ft² = 2S - 2ut

(next step: Since 2 is common in the variables on the right side, we can factorize to have:)

ft² = 2(S - ut)

(next step: Isolating f which is the subject of the formula, we have:)

f = 2(S - ut)/t²

So the final equation below shows we have made f the subject of the formula is:

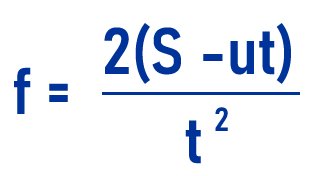
Conclusion

The steps involved in making any variable of an equation the subject are not strictly stated anywhere. It just involves knowing when to move variables around, knowing when to collect like terms, introduce square for square root, cube root for cube and many other steps. It requires critical thinking and letting the process flow along. Once you understand the basic rules of mathematic too, its very easy to make any expressions the subject.

The two examples above and the two in my previous post should be proper guides to anyone that wishes to make a variable the subject. If you have any questions on this subject, I would be willing to answer them in the comment section of this post.