OSCILLATIONS AND MECHANICAL WAVES: Setting up Stationary Waves and The Doppler Effect.

Greetings to all my readers and everyone in general. Starting from where I last stopped in my post on Oscillations and Mechanical waves. In this post, I will explain how to set up stationary waves and the Doppler effect.

SETTING UP STATIONARY WAVES

Stationary waves are set up in stringed instruments such as a guitar. What we see is the string vibrating from side to side. At the moment that the string is plucked, a progressive transverse wave is set up travelling out from that point. It meets the fixed end of the string and is reflected back. The amplitudes of the two waves add together as they meet.

^{Lookangmany, CC BY-SA 4.0}

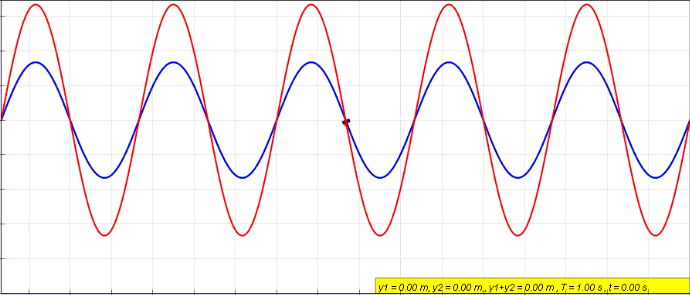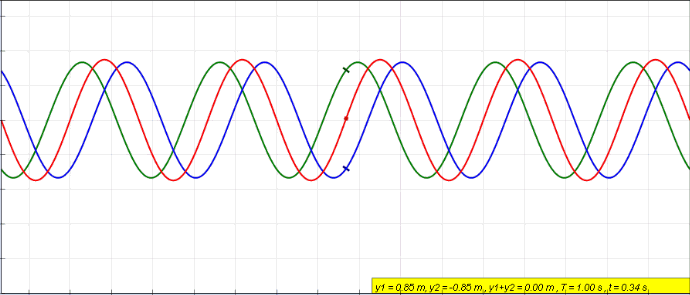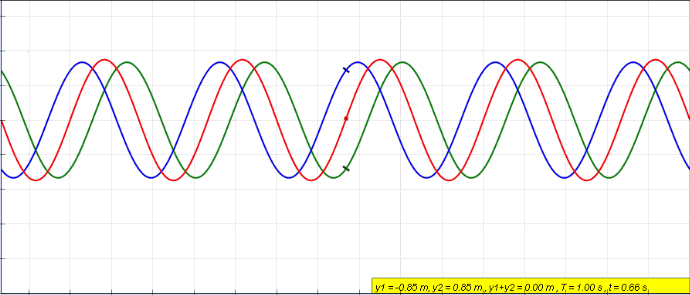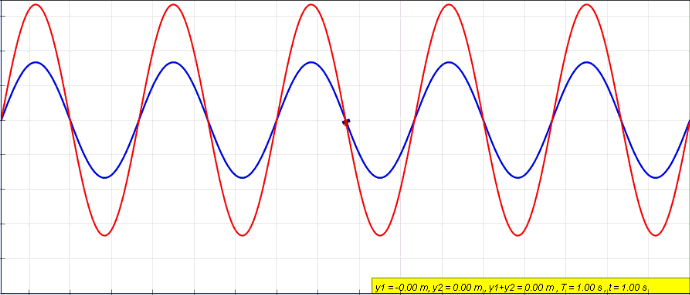
The string moves continuously on its own at some certain frequencies because it is fixed at the two ends. So, after both the outgoing and reflected waves are summed together, a stationary wave will be set up in the string. If the string is plucked in the middle, the fundamental mode will be observed. In this instance, the string vibrates with the greatest movement (displacement) at the middle (known as the antinode) and the displacement drops down to zero at the both ends (this is called the called nodes).

We can investigate stationary waves in the laboratory using a stretched string or a long rubber band. The string is stretched from a fixed support over a pulley and is held taut by a suspended mass as shown in the diagram below. A vibration generator is tied to the string near one end.

The frequency of vibration is altered starting from a low value, usually with little effect on the stretched string. As the frequency increases, the vibration generator reaches a particular frequency at which the string suddenly starts vibrating strongly, see (a). Resonance is occurring. The natural frequency of the string is now equal to that of the vibration generator. This resonance frequency is the fundamental frequency f₀ of the string, sometimes called the first harmonic.

As we increase the frequency of the vibration generator further, oscillation of the string is rapidly reduced. We notice little movement until the generator frequency has doubled to 2f₀. Now the envelope of the string (the shape the vibrating string encloses) has altered. There are three nodes, one at each end and one in the middle, see (b). This means that there are two antinodes positioned a quarter of the string length from each end. These two antinodes are vibrating out of phase and there is a phase difference of pi. This frequency of vibration is referred to as the second harmonic or the first overtone. If we increase the frequency further, we identify other resonant frequencies. The next is 3f₀ with three antinodes on the string, see (c), and so on.

^{An image drawn by me showing the fist, second and third harmonic frequency of a stretched string}

REFLECTED WAVES

Looking in detail at how standing waves can be set up, we can set off a short wave on a slinky spring that has already been strongly fixed at its end. Assuming the wave is composed of one and a half wavelengths, as in the figure (a) shown below. The wave would travel along the spring and stretches out to the far end.

At the far end, the wave can't extend further, so it's reflected back, as in (b). Meaning that the velocity would change sign. Also, the phase of the wave too would change. If the displacement of the forward moving wave is upwards when it reaches the far end, then its displacement would be downwards on reflection. Where the two waves extend over each other, the displacement of the spring would be the summation of the two waves. But, finally, we would see the reflected wave appear fully and pass back along the spring, just as shown in the (c) part of the diagram

^{An image drawn by me showing the forward and reflected waves on a slinky}

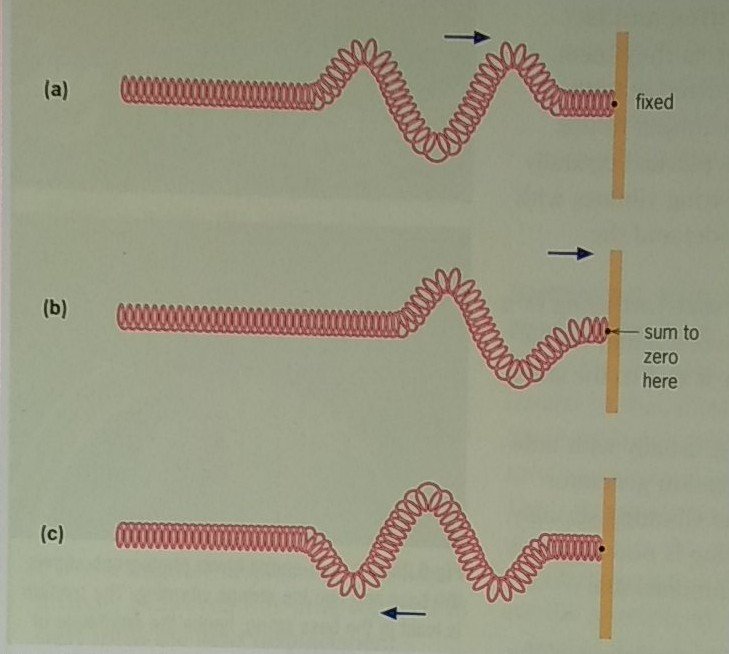
The frequency, velocity and wavelength of the wave all remain the same in reflection. If no energy is lost at the far end, the amplitude of the reflected wave equals that of the incoming one. The phase difference of pi which we have identified and which is illustrated by the figure (a) and (c) is crucial to the setting up of standing waves.

When waves pass through each other, the displacement at any point is the sum of the individual displacements of the two waves passing in opposite directions. Figure (a) shows the relative positions of two waves travelling in opposite directions. Work out for yourself what pattern you will see.

STANDING WAVES ON A STRING

Let us consider a progressive transverse wave on a string with an exact number of complete wavelengths in its length.

It is not easy to see what happens at all times, so let us select certain special times. We start with t =0 when the displacement of the forward wave is maximum at both the initial and far ends, though of course this displacement will be modified by the reflected wave. The figure shows the situation with the forward, reflected and summed waves at this time t = 0, and at a series of times during the first-half period. We could go on to show the waves for the second half-period in a similar way in order to complete the overall pattern. The envelope for all possibilities is shown in the final diagram.

Frequency of standing waves on a string

We have seen that, as there are always nodes at the ends of the string, there must be a whole number, n, of half-wavelengths between each end. With a string length l, this means that: nλ/2 = l or: λ= 2l/n

It can be proved that, if T is the tension in the string and u is the mass per unit length, the velocity c of a wave down a string is given by: c=√(T/μ)

We already know that c = fλ, where f is the frequency of vibration. So: f = c/λ = nc/2l = n/2l × √(T/μ)

STANDING WAVES USING SOUND WAVES OR MICROWAVES

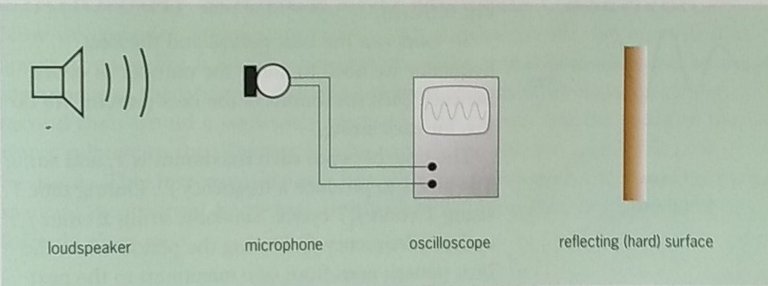
Sound waves are longitudinal waves in air (or another medium) similar to longitudinal waves in a slinky. They consist of compressions and rarefactions in the air. By sending sound waves from a loudspeaker and reflecting them from a hard surface, standing waves are established in the air. There will be regions where the air molecules are vibrating back and forth strongly (antinodes) and other regions where there is no movement of the air (nodes). By moving a microphone between the loudspeaker and the reflecting surface, the variation of displacement can be shown on an oscilloscope.

Instead of a loudspeaker, we can use a microwave transmitter. In this case, instead of a microphone and oscilloscope we then use a microwave receiver and ammeter. A metal plate acts as reflector. Although the experiment is similar, the nature of the waves themselves is very different. Microwaves are electromagnetic waves, which I have explained in some of my posts before.

^{An illustration by me showing a demonstration of standing waves using sound waves}

STANDING WAVES IN AN ORGAN PIPE

These are sound waves and therefore longitudinal waves. They are set up by compression and rarefaction of the air within the pipe. Nodes and antinode occur just as they do for a vibrating string. But there is a difference. In the case of a string, both ends are effectively held fixed in order to establish the standing wave. In an organ pipe, vibrations can be set up either with both ends of the pipe open or with one end closed and the other open. At a closed end there must be a node present, and at an open end there must be an antinode (the air vibrates freely back and forth).

BEATS

Let's assume we adjust two strings of a guitar to vibrate nearly but not the same frequency. When they are strummed at the same time, the volume of their sound produced looks to rise and fall continuously without interruption. Now, this rise and fall in the sound produced has a fixed frequency which is called the beat frequency. The sound waves created by the two guitar strings interact (i.e interfere) and our ears perceive the difference in the resultant intensity. The ears would detect maximum intensity when the waves are added together otherwise known as (constructive interference) and minimum intensity is observed when the waves eliminate each other which is known as (destructive interference).

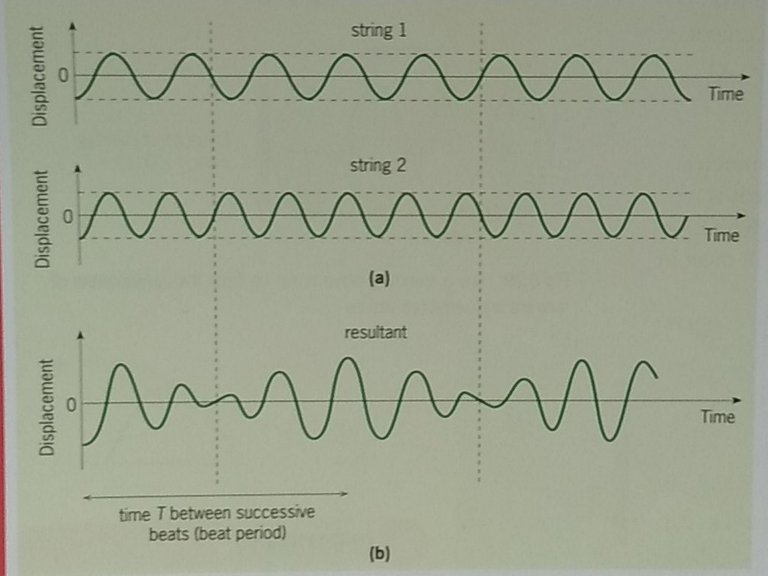
We can see what is happening by adding together the two separate waves as shown in the diagram below. The resultant, obtained by the principle of superposition, is also shown in figure (b). To work out the beat period and the beat frequency we need to know the number of cycles between each maximum of the beat pattern. We do this for each string.

The time between each maximum is T, and string 1 is tuned to produce a frequency f₁. During time T, string 1 emits f₁T cycles. Similarly, string 2 emits f₂T cycles at frequency f₂. During the period when the beat pattern goes from one maximum to the next maximum there must be one cycle difference between the waves from the two strings. The waves start in phase at the maximum, gradually go out of phase, and come back into phase, with a difference of one cycle (and only one cycle). Therefore: f_B = f₂-f₁

^{An illustration by me showing the setting up of beats}

THE DOPPLER EFFECT

So far I have talked about setting up waves and the need to observe or detect them. In the case of transmitted sound waves one can use a microphone connected to a loudspeaker or oscilloscope to detect them. Let's assume that when this is done, both the emitter of the sound waves and the detector are stationary. But what happens if one is moving relative to another? Is our observation changed in any way? Let's take the case of radar waves and that the police use the effect to determine the speed of motorists, as an instance. Here we look at the effect,called the Doppler effect, in more detail. The effect is not restricted to electromagnetic waves, as you will realise if you listen to the siren on a police car or ambulance as it approaches and then travels away. The Doppler effect is the change in frequency produced when a source of waves moves relative to the observer, although there must be a component of the movement directly towards or away from the observer or source.

^{Lookang, CC BY-SA 3.0}

STATIONARY SOURCE AND STATIONARY OBSERVER

The figure below shows the sound waves emitted by a source S at a speed v and a frequency f. This is the frequency heard by the observer O when both are at rest. We also assume that the medium is air and that it is not moving. In fact, we shall assume that the air is not moving in all cases we consider. Below the figure, the observed wavelength λ’ is denoted and here this is the same as the wavelength of the sound emitted.

STATIONARY SOURCE AND MOVING OBSERVER

Now we consider a stationary source with an observer moving towards it at speed v. The wavelength of the sound is not affected by the movement of the observer. But the observer crosses more wave crests per second than would a stationary observer. This means that the speed of the waves relative to the observer has increased. The relative speed will now be v + v₀. This increase of speed, but with the wavelength the same, means an increase in observed frequency. If this observed frequency is f’, the wave formula gives us: v + v₀ = f’λ or f'= v + v₀/λ

The frequency as emitted by the source is f = v/λ, so the ratio of frequencies is: Observed frequency/Source frequency = f'/f = v + v₀/v

If the observer is moving towards the source, the observed frequency increases. If the observer is moving away from the source then fewer crests are crossed per second and finally If the observer is moving away from the source the observed frequency decreases.

STATIONARY OBSERVER AND MOVING SOURCE

In the figure showing what happens when the source is moving towards a stationary observer at a steady speed vs. The effect is to reduce the wavelength, because in a given time more waves fill the space between source and observer than when both are at rest. The observed frequency thus increases – the observer is passed by more crests in that time. But the waves pass at the same speed.
The observed frequency is f’ and there is, as a consequence, an observed wavelength λ’, which is different from the actual wavelength at the emitter: λ'=v/f', hence f'=f[1/(1-v_s/v)]

This confirms that: when the source moves towards the observer, the observed frequency increases. If the speed of the waves is very large, as in the case of electromagnetic waves (i.e. v >> v_s), then the formula again becomes Δf = fv₀/v.

If the source is moving away the formula becomes: f'=f[1/(1 + v_s/v)]

When the source moves away from the observer the observed frequency decreases.

BOTH SOURCE AND OBSERVER MOVING

One can now deduce from the above analysis that if both the source and the observer are moving then the observed frequency will be f'= f[v ± v₀/v ± v_s]

Where I use:
+v₀ when observer is approaching source
-v₀ when observer is receding from source
-v_s when source is approaching observer
+v_s when source is receding from observer

You may wish to check that this formula reduces to the appropriate earlier equations. Motion towards each other increases frequency; motion away decreases frequency.

SUMMARY

After reading through all my posts on Oscillations and Mechanical waves starting from 1, 2, 3 and this concluding chapter you should now understand the following concepts and be able to use the following equations:

• The meaning of amplitude A, period T and frequency f of a wave and the relationship T = 1/f = 2π/ω.
• The meaning of speed v and wavelength l of a wave and the relationship v = fλ.
• A mechanical wave needs a medium through which to pass. Waves may be longitudinal or transverse.
• The period of a simple pendulum is given by T = 2π√(l/g) and the period of a mass-spring system is given by T = 2π√(m/k)
• In simple harmonic motion (s.h.m.), acceleration is directly proportional to displacement from a fixed point and directed towards this point: a = -w²x.
• The velocity of a mass m under s.h.m. is given by v = ±w√(A²-x²)
• The meaning of the terms: oscillator, displacement node, antinode, harmonic, overtone, phase difference, damping.
• There is a transfer of energy between kinetic and potential forms during s.h.m.
• The difference between stationary (standing) and progressive (travelling) waves.
• Energy can be exchanged between a driving system and a driven vibrating system. Resonance occurs when their frequencies are equal.
• The superposition of two waves of almost equal frequencies f₁ and f₂ where f₂ > f₁ produces beats of frequency f₂ – f₁.
• If the source of a wave and an observer are moving relative to each other, there is a Doppler shift of frequency. Motion towards increases the frequency; motion away decreases the frequency.

Thanks for reading.

REFERENCES

https://en.wikipedia.org/wiki/Reflection

https://en.wikipedia.org/wiki/Standing_wave

http://hyperphysics.phy-astr.gsu.edu/hbase/Class/PhSciLab/string2.html

http://physics.bu.edu/~duffy/EssentialPhysics/chapter21/section21dash10.pdf

https://www.ck12.org/book/cbse_physics_book_class_xi/section/14.6/

https://www.physics-and-radio-electronics.com/physics/beats-waves-physics.html

https://www.physicsclassroom.com/class/sound/Lesson-3/Interference-and-Beats

https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics

https://en.wikipedia.org/wiki/Doppler_effect