NEWTON’S LAW AT WORK: Explanations on The Gravitational Potential, Escape Velocity and The Movement of Satellites in Orbits.

The gravitational potential (V) of an object at a point in space is a useful idea. It allows us to calculate the energy changes, or the work done, when a satellite moves to a different orbit. Gravitational potential can be compared to the concept of electrical potential, and is defined as follows:

Gravitational potential is the change in potential energy for a unit mass that moves from infinity to a point at less than infinity in a gravitational field.

If we make r₂ = infinity, r₁ = r and m = 1 (kg), the potential energy difference formula simplifies to:

V = -GM/r

For the field of the Earth, we can use this formula to calculate the potential at a point at a distance r from the centre of the Earth. A typical meteorite enters the Earth’s atmosphere at about 20 km/s, almost double the speed calculated in the example of my previous [post](link). This is because meteorites are already moving when they start falling towards the Earth, and the Earth is also moving. We have also ignored the gravitational effect of the Sun, which is very large.

^{Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body. AllenMcC, CC BY-SA 3.0}

ESCAPE SPEED

Looking the other way round at the example, we can see that if an object is at rest on the Earth’s surface, we would have to give it some kinetic energy before it could escape completely from the Earth.

To reach infinity where the Earth’s gravitational field doesn’t affect it, we would have to give it 6.3 × 10⁷ J of kinetic energy for every kilogram of its mass. This would convert the negative gravitational potential it had on the Earth’s surface (to GPE per unit mass), of value -GM/r_E, to zero.

You should now use the kinetic energy formula to check what is obvious that each kilogram of an object has to be given the right amount of energy to reach a speed of 11.2 km/s – in the right direction – for it to be able to escape from the Earth. This speed is called the escape speed (or escape velocity).

EXAMPLE

The Moon has a mass of 7.3 × 10²² kg and a radius of 1.7 x 10⁶ m. What is the escape speed for an object on the Moon?

Answer: The gravitational potential at the Moon’s surface is:

-GM/r_M = -(6.7 × 10^-11) × (7.3 x 10²²)/ 1.7 x 10⁶

= -2.88 × 10⁶ J kg^-1

Any object has to be given an equivalent quantity of kinetic energy per unit mass to escape the Moon’s gravitational pull.

So, kinetic energy per kilogram is:

½ v² = 2.88 × 10⁶

v² = √ (2 x 2.88 × 10⁶)

v = 2.4 x 10³ m/s

Escape speed, v = 2.4 × 10³ m/s.

MOVING IN AN ORBIT

The simplest orbit for an Earth satellite is circular, centred on the Earth’s centre. A typical satellite used to monitor the Earth’s surface has the circumpolar orbit. While the satellite orbits, the earth spins underneath it. So, if a complete orbit takes 2 hours, the satellite will overfly the whole of the Earth in 12 orbits. Newton explained how, in theory, an object shot at great speed from the Earth’s surface could become an orbiting satellite. He imagined a cannon on a mountain, firing cannon balls parallel to the Earth’s surface at ever-increasing speeds. Each ball lands further from the cannon than the previous one, travelling in a curved path. Newton imagined that, eventually, the curved path of a ball would match the curvature of the Earth and then the ball would be in orbit.

It is of course the force of gravity acting on a cannon ball that makes it fall back to Earth. A ball which remains in orbit also experiences this force. Its speed may be constant, but it still obeys Newton’s second law of motion because its velocity continuously changes – the direction of the ball’s motion is always changing. The force of gravity is responsible, making the orbiting ball accelerate towards the centre of the Earth – in free fall.

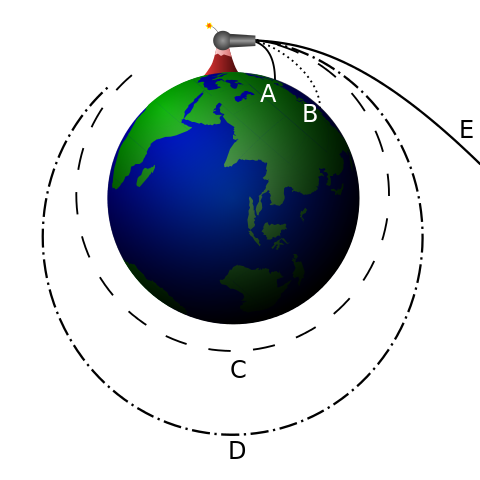
All orbiting satellites are in free fall. Their acceleration is equal to the value of g at that distance from the Earth, and this acceleration is directed towards the centre of the Earth. Clearly, the speed of a satellite has to be just right to stay in a circular orbit, if it is too slow, the satellite falls to Earth like the ‘unsuccessful’ cannon balls. Too fast, and the satellite’s orbital radius increase, or its orbit may become an ellipse. Much too fast, and the satellite leaves Earth's orbit completely.

EARTH SATELLITES PROVIDE REMOTE EYES AND EARS

The fact that Earth satellites can be put into orbit fairly cheaply has revolutionized everyday communications and information systems. On our television screens, we can now see events unfold in the remotest parts of the world as they happen. All a news reporter needs is a small dish aerial and a portable power supply, and access to a communications satellite. These satellites are in a high, geosynchronous orbit above the equator.

Communications satellites also carry international telephone messages that are far clearer than those transmitted by the old radio or landline systems. Communications describe how information is sent as radio waves between satellites and ground stations, and explains the digital technology that allows a huge number of messages to be transmitted at the same time.

Weather satellites provide the pictures of cloud systems we see on television weather reports. These satellites have polar orbits and are closer to the ground than geosynchronous satellites. The recording of land and sea temperatures, and the forecasting of climatic changes and trends in the greenhouse effect, have all become much more reliable, thanks to weather satellites. It was a British satellite collecting data over Antarctica that first provided evidence of a ‘hole’ developing in the ozone layer.

Links between satellite and ground computers allow us to know the positions of satellites very accurately. Similarly, satellites give us precise positions for objects on Earth, especially using the GPS. For many years, ships and aircraft have relied on navigation satellites to pinpoint their locations. On land, small receivers are now easily and cheaply available which use navigation satellite data to tell mountain walkers where they are to the nearest few metres, and drivers of vehicles their exact locations, and even the routes to take to avoid traffic jams. Bus companies use them to check where their buses are and so adjust their speeds to avoid ‘bunching’.

Military satellites keep an eye on the movement of ships, troops and vehicles. They can detect when weapons are being fired, and can eavesdrop on conversations over a wide range of electronic communications systems.

^{The International Space Station orbits above Earth. NASA, Public Domain}

The infrared satellite sensors which detect land and sea temperatures can also monitor the growth of crops whether they are healthy or diseased, or lack water, for example. In the European Union, agricultural land is monitored to check that farmers who claim money for leaving land uncultivated (‘set aside’) are not, in fact, growing crops on it.

Satellites are sent into orbit either by rocket systems used once only, such as the European Ariane, or by the reusable US Space Shuttle. An increasing number of countries are putting satellites into orbit, for their own national uses such as weather monitoring, or on a commercial basis, hiring out the satellite facilities to research and communications organizations such as universities and television companies.

Formula for the inward acceleration of an object moving in a circle.

The formula developed here applies to any object moving in a circle – for example, the rim of a wheel, a ball whirling on the end of a string, a car going round a bend or a satellite in orbit.

Let’s assume two positions, A and B, of a satellite moving in a circle round the Earth at constant speed v. The radius line, r, moves through an angle, θ, measured in radians, in a time t, and the object moves a distance rθ. The gravitational force always acts along a radius, inwards towards the centre of the Earth. In a figure showing how the vector representing the velocity of the satellite has changed in time t. Since the speed of the satellite doesn’t change, vectors v_A and v_B of equal length.

Δv shows the change in velocity using a triangle of vectors such that:

V_B = v_A + Δv

In these two diagrams the value of t, and therefore of 0, is large. Now see Fig 3.20, in which is very small, so that Δv is also very small. This also means that the time involved is small.

The acceleration of the body is given by

a = Δv/t……… [eqn 1]

We can see that the object covers a distance rθ in time t at a speed v, so that

v = rθ/t hence 1/t = v/rθ………… [eqn 2]

Substituting for 1/t in equation 1 gives:

a = vΔv/rθ………. [eqn 3]

v is directed along a tangent to the circle, so is always at right angles to the radius line. (Note that for small θ, sin θ = tan θ = θ radians.) When the radius turns through an angle θ so does v. So, with the usual small-angle approximation:

Δv = vθ……….[eqn 4]

Substituting for Δv in equation 3 gives:

a = v²/r………[eqn 5]

As angle θ gets smaller and smaller, the direction of Δv becomes closer and closer to being at right angles to v. This means it is in the direction of the radius and acting towards the centre of the circle. This is, of course, the direction of the force causing the acceleration.

We can therefore represent the centripetal force F required to keep a body of mass m moving in a circle, using the relation:

Force = mass × acceleration 

F = mv²/r

SPEED AND THE RADIUS OF THE ORBIT

A satellite that moves in a circular orbit has an inward gravitational acceleration g and speed v, which are linked by the equation:

g = v²/r………….[eqn 6]

where r is the radius of the orbit.

SPEED OF A SATELLITE IN A CIRCULAR ORBIT

A satellite in polar orbit sweeps over certain areas of the Earth which depend on the number of its orbits in 24 hours, hence on its speed. The speed is set before launch, so that the orbital time matches the purpose of the satellite – whether it is a near-Earth weather monitoring satellite, or a distant communications satellite, for example.

The satellite’s speed depends both on the radius of its orbit and on the strength of the gravitational field at that height. A typical height for a satellite in near-Earth orbit is 100 km. This gives an orbital radius of 6.47 × 10⁶ m. The inward acceleration is the value of g at that height, which is 9.53 m/s². Thus, from equation 6 above, its speed is:

v = √gr

Hence, v = 7.85 km s^-1

The circumference, 2πr, of its orbit is 4.07 × 10⁴ km. The satellite, therefore, completes an orbit in 86.3 minutes.

GEOSTATIONARY SATELLITES

Communications satellites are put into geostationary or geosynchronous orbits, meaning that the satellites stay still relative to the Earth. As a result, ground aerials which send and receive data to and from a satellite need only point in one direction, rather than having to steer to follow the satellite.

To be geostationary, an orbit has to be directly above the equator, and the satellite must complete its orbit in exactly the same time as the spot underneath rotates through its orbit, namely 24 hours. In theory, a geostationary satellite ‘keeps up with’ the point on the rotating Earth. In practice, its position shifts a little, as the satellite’s speed is affected by slight changes in the Earth’s gravitational field. Small adjuster rockets are fired to regain the correct position.

Using equation 6 above, we can calculate the height at which a satellite must orbit in order to remain geostationary.

Let the radius of the orbit be r_s. The satellite must have an orbital speed v such that:

2πr_s = vt = v × 86 400 (t is 24 hours = 86 400 seconds)

So,

v = 2πr_s/86 400………. [eqn 7]

From equation 6.

v = √gr_s ………… [eqn 8]

At distance r_s

g = GM/r_s²

Putting this value for g into equation 8.

v = √(GM/r_s)

Equating the expressions for v in equations 7 and 8, we have:

2πr_s/86 400 = √(GM/r_s)

Inserting the values of constants G and M, we get a value for the radius, r_s, for a geostationary orbit of 4.23 × 10⁷ m. This is over six times the radius of the Earth and, at that distance, the value of g is 0.223 N/kg.

I will be stopping here for now. In my next post, I will discuss the physics behind putting satellites into orbit, weightlessness, rockets and jet engines. Till then, I remain my humble self, @emperorhassy. Thanks for coming.

REFERENCES

https://opentextbc.ca/physicstestbook2/chapter/gravitational-potential-energy/ 

http://hyperphysics.phy-astr.gsu.edu/hbase/gpot.html 

https://en.wikipedia.org/wiki/Gravitational_potential 

http://www.softschools.com/formulas/physics/escape_velocity_formula/90/ 

http://www.qrg.northwestern.edu/projects/vss/docs/space-environment/2-whats-escape-velocity.html 

https://en.wikipedia.org/wiki/Escape_velocity 

https://www.jstor.org/stable/41142692 

https://www.tandfonline.com/doi/abs/10.1080/0143116031000101558 

https://crisp.nus.edu.sg/~research/tutorial/intro.htm 

https://www.physicsclassroom.com/Class/circles/u6l1e.cfm 

https://en.wikipedia.org/wiki/Circular_motion

https://socratic.org/questions/a-satellite-moves-around-the-earth-in-a-circular-orbit-with-constant-speed-expla

https://en.wikipedia.org/wiki/Orbital_speed

https://science.howstuffworks.com/satellite6.htm

https://www.dummies.com/education/science/physics/how-to-calculate-a-satellites-speed-around-the-earth/

https://www.youtube.com/watch?v=nxD7koHdQhM

https://www.physicsclassroom.com/class/circles/Lesson-4/Mathematics-of-Satellite-Motion

https://en.wikipedia.org/wiki/Geostationary_orbit

https://en.wikipedia.org/wiki/Geosynchronous_satellite