Math Math Math

Numbers govern the world around us. From the economy to engineering into the very bones of society itself. Even your TV would not work if someone hadn't figured out that coiling wire into a solenoid creates a constant magnetic field. Technology is everywhere, and we tend to not give it a second thought until the thing breaks and we're left wondering why.

One such common mathematical discussion is the one of P vs NP.

That's Polynomial vs Non-Polynomial.

For those of you who have forgotten your quadratic equation (I know I have) a polynomial might look something like this:

x^2 + 5x - 7

The basic gist of it is that polynomials lack exponents as a variable. x squared is a polynomial even though it contains an exponent, but 2^x (two to the x power) is non-polynomial because the exponent is going up on the x-axis.

For many this would not appear to be a big deal at first glance, but the ramifications of the math are literally world-changing. The entire field of cryptography hinges on the fact that the difficulty of solving the problem is exponential. Considering most of us are quite deep into this whole crypto thing: math like this can become relatively pertinent information.

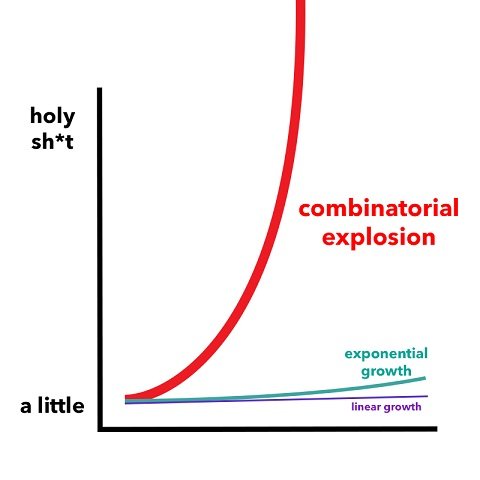
Why don't they just call it exponential vs non-exponential?

Ah well nerds gonna nerd aren't they? Something like a factorial is technically not exponential growth but still belongs in this same category of non-polynomial complexity. In fact a factorial increases in complexity even faster than normal exponential growth, as we can see in the extremely deceptive graph above in which exponential growth is labeled "a little".

What is a factorial?

Something like 10! Er, not 10 the number + an exclamation point but ten factorial. 10 factorial (10!) means starting with 10 and then multiplying it by every integer lower than 10 until getting down to 1. So...

10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

Given this definition we can see that factorials increase even faster than exponents, because something like 2^x is only ever going to double on the next round, while a factorial will double, triple, and then quadruple and so on. In fact, the most famous non-polynomial problem of all time just happens to also be one of factorial complexity.

The Traveling Salesman Problem

Surely this is the most famous NP problem. Much like the Byzantine General's problem in crypto the example tries to base itself in reality but is much more relevant to the mathematical and digital realm. Does a real traveling salesmen have to worry about this problem? Not really. But computer programmers certainly do!

The Traveling Salesman Problem is quite simple:

• The salesman needs to visit some number of cities (n).
• The salesman wants to plan the trip efficiently.
• What order should they travel in for the shortest total distance?

To anyone who doesn't fully understand NP problems this will sound like a trivial task, especially for a computer that can make a trillion computations a second. But if we actually try to complete the task programmatically the problem reveals how impossible it is as the number of cities (n) continues to grow.

At first, with only one city to travel to, there is only one option. Adding the second city creates two options, while adding the third city creates six options and a forth creates 24. Every option that gets added multiplies the number of options by the next factorial in the sequence. If there were 20 cities the number of brute-force paths available would be 20! or 2,432,902,008,176,640,000... which is 2.4 quintillion possibilities. At a trillion computations a second this would take 2.4 million seconds to solve... also known as 28 days.

Of course you can see in the comic above that there is apparently a way to reduce the n! complexity down to n^2*2^n, which is still quite exponential but also somehow much easier to solve. In this case 20 cities would be reduced from 2.4 quintillion options for factorial brute force down to 419,430,400 using the n^2*2^n shortcut, which is obviously quite impressive and possible for a computer to solve. We'd go from 28 days to under 1 second.

Heuristics & Chess example

Computers used to be quite bad at chess back in the day but now are practically unbeatable. How did this happen? Heuristics. If we think of all possible moves in chess as a tree, that tree expands at a non-polynomial complexity just like all these other problems. If we have 20 moves available and our opponent also has 20 moves available then trying to think even 3 moves ahead can be quite difficult.

However, the way we get around this overwhelming complexity is to prune the decision tree and eliminate dead-ends that lead to outcomes that we don't want (in this case losing the game). It's known in chess that the queen is the best piece. Therefore sacrificing your queen is going to be a bad move 99% of the time. Instead of trying to brute-force the solution and dedicating resources to dead-end paths we employ heuristics to prune the tree and simply ignore that path entirely.

This is a double-edged sword because if the heuristics being used are flawed than it will delete the correct answer (checkmate). The goal becomes a balance of making sure to eliminate only the worst solutions and trying to check everything else if possible.

I took an AI class in college and have actually employed this method myself in a program I created that would solve Sudoku puzzles. The assignment was to create a Sudoku game with a 9x9 option and a 16x16 option (using hexadecimal). The 9x9 could be brute forced and the answer found (although it could be slow). However the 16x16 version would completely lock up the computer... I think I calculated it would have taken my computer 3 days to solve... lol.

However on this particular assignment I went above and beyond and created the ultimate Sudoku solver using heuristics to prune the decision tree. I even created advanced x-wing logic (you can look it up if you want) because I found the project of particular interest. I bet I've written about this in 2018 let's see if I can find it... nope I can't... hm maybe I'll go dig up that code one day... it's written in Java.

Han Solo?

It's the ship that made the Kessel Run in less than 12 parsecs.

Many of us will never forget this timeless moment in cinema where Han Solo is trying to brag about his ship. Of course a "parsec" is 3.26 lightyears... so a parsec is is not a measurement of speed but rather one of distance, thus many a nerd points this out as a comical flaw of the entire logic of such statements. Classic tactic of using scientific words in movies that people don't understand but sound smart within the contexts of the situations that the characters are tangled in.

The flux capacitor needs more dilithium crystals!

Of course I was quite impressed when I read that some other nerd's counterpoint to this is that we can apply the Traveling Salesman's problem to Han's words. Perhaps the ship's engines themselves aren't as good as the AI, navigation, evasion, and the computer systems needed to traverse through the black void of space. An interesting thought to be sure: that what he said was actually 100% accurate (or that he was simply trying to smooth talk them).

Also what kind of crypto does this galaxy use?
Where can I find these units?

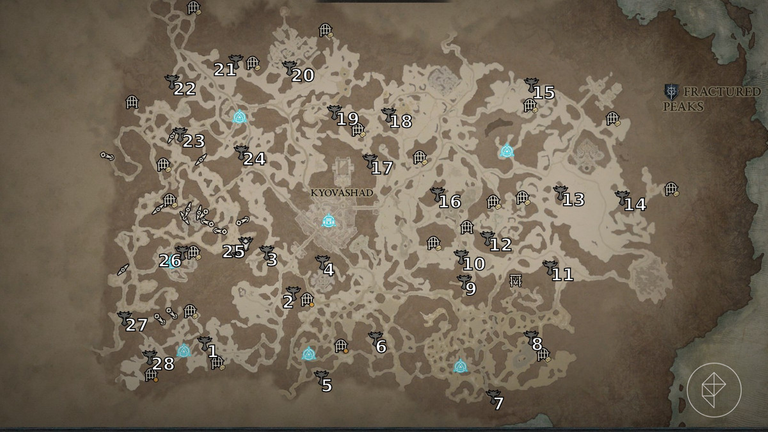
Hilariously enough the only reason why I write this post to begin with is that playing Diablo 4 remined me of the Traveling Salesmen problem when trying to find these altars. Notice how they are all numbered for convenience on a path? Rest assured that it's impossible that this path is the most efficient one for all the reasons I've described above. The paths that people have chosen to get the altars is totally random and certainly not the quickest solution.

O(n)

In programming, the notation for discussing these complexities comes in the form of ORDER n which is O(n) for short. If we are traversing a list and have to check every item in the list then the complexity is O(n). If we only have to check half of the list on average then the complexity is still O(n) as this number is largely generic and gets rounded to the closest match.

• O(1) means we only have to check one time.
• O(n) is linear complexity.
• O(n^2) is polynomial complexity.
• O(2^n) is exponential complexity.
• O(n!) is factorial complexity.
• O(log(n)) is logarithmic complexity (which is the best one right behind O(1)).

It is possible to do extra work to take an O(n) or O(n^2) solution and turn it into something more efficient. A binary search algorithm on a sorted list can reduce the number of checks from O(n) to O(log(n)). So instead of needing to check every single entry you just have to check the halfway point and continue cutting the list in half until we find the answer. Bitcoin isn't the first solution to have a halving event, and it won't be the last.

This becomes worth it as the list gets larger, as a list with a billion entries in it will take half a billion checks on average with O(n) but only 30 checks with the log base two solution. Unfortunately a binary search requires the list to be sorted in a programmatically understandable order (like alphabetical or greatest to least value). This becomes a balancing act as it might be more expensive to keep the index sorted if items are constantly being added or removed from memory.

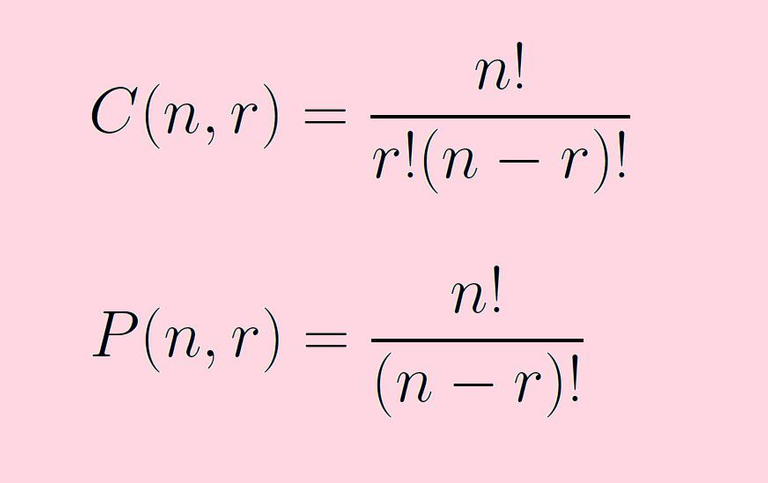
Permutations and Combinations

This is the final example I have for non-polynomial problems. Permutations and combinations are two of the most important concepts in statistics. As it turns out: statistics is one of the most practical mathematics that actually applies to the real world. We should all know this stuff inside out but it seems like academia likes to focus on other things that have very little real-world relevance. Typical academia.

In any case a permutation is when the order of elements matters. The most classic example is a password or even your crypto private keys. The characters need to be placed in the exact correct order for the solution to be found. As we can see above the complexity of both P & C are factorials which is why passwords are so impossible to crack given a long length and wide variety of characters.

A combination is where the order does not matter, and will often come in the form of something like 10 choose 4 which would be notated as C(10,4). In that particular case there are 10 total options to choose from, you can't choose the same element twice, and you get to choose 4 times. For example if you wanted to make dinner using 4 ingredients out of 10 available the number of possibilities would be C(10,4) or 210 different meals.

Not the best or most relevant example, but good enough.

Combinatorial complexity occurs quite often in gambling which is why I have a particular interest in it. Given another example in this vein: a deck of cards can never have the same card pulled from it... and the order of the cards has no affect on poker or blackjack. Thus all card games are essentially combinatorial in nature.

When NP works in our favor

In the case of the Traveling Salesman problem it is just that: a problem that we need to solve but can't when the numbers get too big. However, as I have already pointed out, non-polynomial issues can work in humanity's favor as well instead of being a problem. Again, the entire foundation of cryptography only works because the complexity is NP.

Another example of this would be technology itself.

There's a reason why computers keep getting exponentially faster and cheaper over time, and a lot of that is rooted in these NP issues. Once we automate some chip to perform a certain task, the jump toward getting it twice as fast and half as cheap is shockingly easier than many would assume without any background knowledge.

Transistors themselves are either on or off. This can be represented by zero or one, true or false, or any other binary description. One bit can carry two points of data (2^1) but 16-bits can carry 65,536 unique messages, while 128 bits creates a number that is 39 digits long and must be represented in scientific notation. Every time we add a single bit the number of unique combinations doubles, and that's a very good thing for the progression of electronics and technology as a whole.

Conclusion

It's all a bit complicated, but the P vs NP discussion is a very important one in terms of almost all technological advancements and problem solving therein. There's a reason why AI has only just recently become and thing, and again that reason is NP complexity. However, using the proper heuristics and shortcuts we can still achieve the desired outcomes while drastically cutting down a huge problem into something possible to solve.

At the end of the day exponential numbers and complexity are quite unnatural and often do not make sense to the human brain unless we really dive deep into it and put in the effort to learn more. The universe is exponentially complex, but our local environments usually are not. It's our job as a species to ensure that the exponential growth that we are fostering doesn't turn out to be a cancer. Unfortunately this is easier said than done.