Physics - Classical Mechanics - Simple Pendulum

almost 3 years ago

Introduction

Hey it's a me again @drifter1 with the first post of the year 2022! I hope it started great for all of you, and best wishes for the new year!

Today we continue with Physics, and more specifically the branch of "Classical Mechanics" in order to get into Simple Pendulums.

So, without further ado, let's get straight into it!

Simple Pendulum

Periodic motion is not limited to simple harmonic motion (SHM) that we covered up to this point! Of course, not all periodic motion systems have to contain springs.

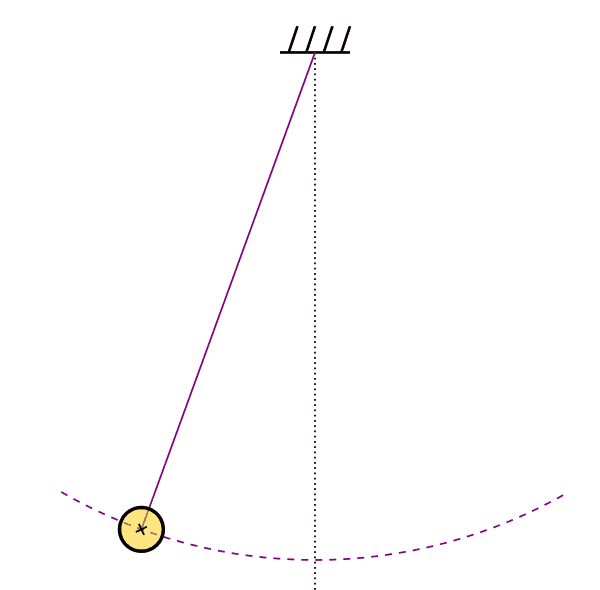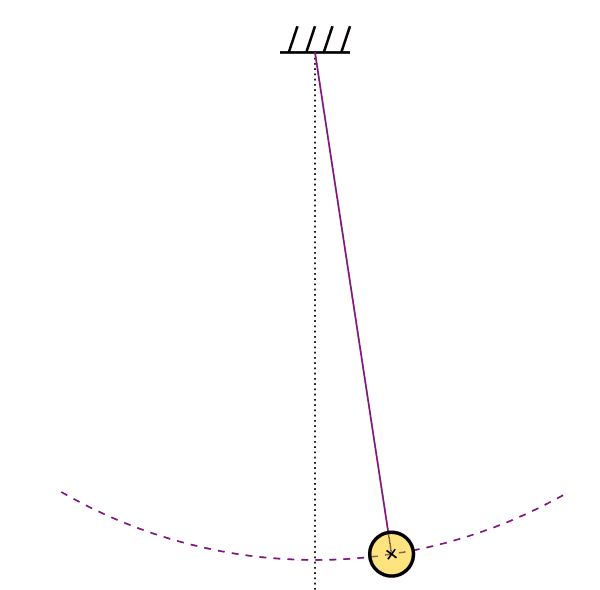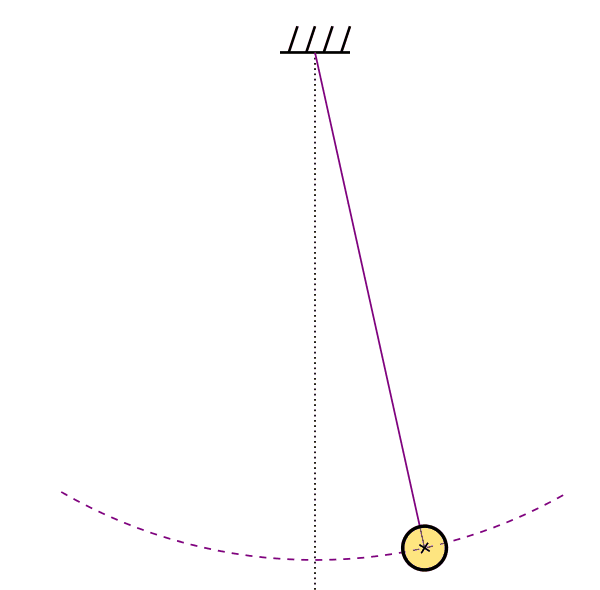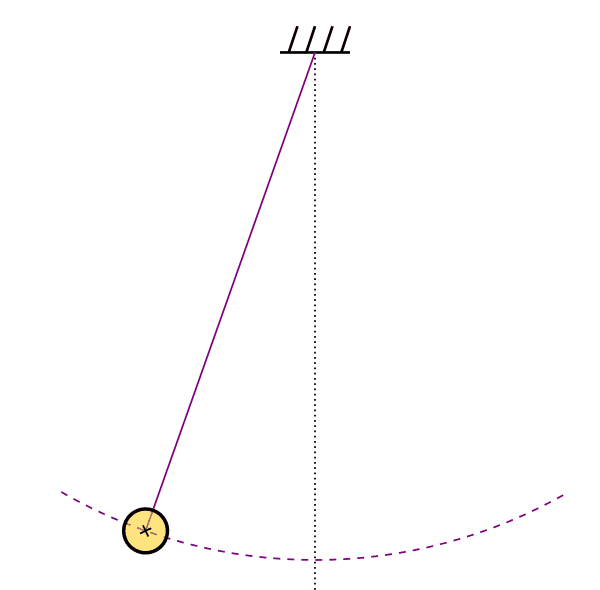
The simple pendulum is yet another idealized model for periodic motion. In such a system, a point mass m is hanging from a weight-less and non-extensible string within a homogeneous gravity field. Moving the mass from the equilibrium position to one side causes an oscillation (or periodic motion) around the equilibrium position.

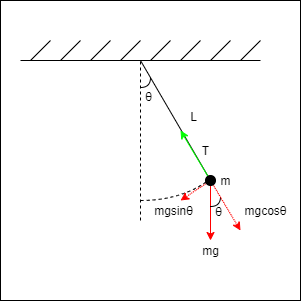
Return Force

The oscillation "route" in the case of a pendulum is not linear, but a circle arc. An arc from a circle with a radius equal to the length of the string, commonly denoted L.

If θ is the angular displacement from the vertical equilibrium position, then the component of the gravitational force that acts upon that route, and so the return force, is given by:

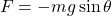
This also proves that such a periodic motion is not simple harmonic motion, as the return force is not proportional to x or at least θ, but instead sinθ.

Small Angle Approximations

When θ is very small, we can approximate sinθ with θ, which gives us:

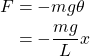
and so an equation of the form F = -kx, where mg/L plays the role of the k spring constant.

This allows us to approximate pendulum oscillation as if it was simple harmonic motion (!) and gives us equations such as:

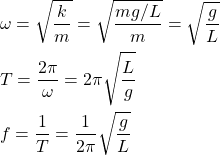
These equations don't dependent on the mass of the object, but only of the length of the string, L.

Using these, we could also approximate the angular displacement as:

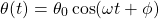
More Accurate Period

Let's also mention how one would approach getting more accurate results! The period can be expressed as an infinite series of the form:

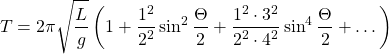
where Θ is the maximum angular displacement (basically the amplitude).

For example, for Θ = 15° the difference between the approximation and this series is only about 0.5%, so the approximation can be considered quite sufficient!

Gravity Approximation

It makes sense to use a pendulum in order to approximate the acceleration of gravity, as the period and length can be calculated easily and with great accuracy!

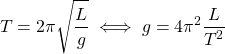
RESOURCES:

References

Images

https://commons.wikimedia.org/wiki/File:Pendulum-no-text.gif

Mathematical equations used in this article, where made using quicklatex.

Visualizations were made using draw.io.

Previous articles of the series

Rectlinear motion

Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion

Plane motion

Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions

Newton's laws and Applications

Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises

Work and Energy

Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
Internal Energy and Work -> Internal Energy, Internal Work

Momentum and Impulse

Conservation of Momentum -> Momentum, Conservation of Momentum
Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
Collision Examples -> Various Elastic and Inelastic Collision Examples
Impulse -> Impulse with Example
Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis

Angular Motion

Angular motion basics -> Angular position, velocity and acceleration
Rotation with constant angular acceleration -> Constant angular acceleration, Example
Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
Parallel Axis Theorem -> Parallel axis theorem with example
Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
Angular Momentum -> Angular Momentum and its conservation
Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
Exercises around Angular motion -> Angular motion examples

Equilibrium and Elasticity

Rigid Body Equilibrium -> Equilibrium Conditions of Rigid Bodies, Center of Gravity, Solving Equilibrium Problems
Force Couple System -> Force Couple System, Example
Tensile Stress and Strain -> Tensile Stress, Tensile Strain, Young's Modulus, Poisson's Ratio
Volumetric Stress and Strain -> Volumetric Stress, Volumetric Strain, Bulk's Modulus of Elasticity, Compressibility
Cross-Sectional Stress and Strain -> Shear Stress, Shear Strain, Shear Modulus
Elasticity and Plasticity of Common Materials -> Elasticity, Plasticity, Stress-Strain Diagram, Fracture, Common Materials
Rigid Body Equilibrium Exercises -> Center of Gravity Calculation, Equilibrium Problems
Exercises on Elasticity and Plasticity -> Young Modulus, Bulk Modulus and Shear Modulus Examples

Gravity

Newton's Law of Gravitation -> Newton's Law of Gravity, Gravitational Constant G
Weight: The Force of Gravity -> Weight, Gravitational Acceleration, Gravity on Earth and Planets of the Solar System
Gravitational Fields -> Gravitational Field Mathematics and Visualization
Gravitational Potential Energy -> Gravitational Potential Energy, Potential and Escape Velocity
Exercises around Newtonian Gravity (part 1) -> Examples on the Universal Law of Gravitation
Exercises around Newtonian Gravity (part2) -> Examples on Gravitational Fields and Potential Energy
Explaining the Physics behind Satellite Motion -> The Circular Motion of Satellites
Kepler's Laws of Planetary Motion -> Kepler's Story, Elliptical Orbits, Kepler's Laws
Spherical Mass Distributions -> Spherical Mass Distribution, Gravity Outside and Within a Spherical Shell, Simple Examples
Earth's Rotation and its Effect on Gravity -> Gravity on Earth, Apparent Weight
Black Holes and Schwarzschild Radius -> Black Holes (Creation, Types, How To "See" Them), Schwarzschild Radius

Periodic Motion

Periodic Motion Fundamentals -> Fundamentals (Period, Frequency, Angular Frequency, Return Force, Acceleration, Velocity, Amplitude), Simple Harmonic Motion, Example
Energy in Simple Harmonic Motion -> Forms of Energy in SHM (Potential, Kinetic, Total and Maximum Energy, Maximum Velocity), Simple Example
Simple Harmonic Motion Equations -> SHM Equations (Displacement, Velocity, Acceleration, Phase Angle, Amplitude)
Simple Harmonic Motion and Reference Circle -> SHM and Smooth Circular Motion, Reference Circle
Simple Harmonic Motion Exercises -> 2 Complete Examples on Simple Harmonic Motion