Physics - Classical Mechanics - Bernoulli’s Equation

[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Physics, and more specifically the branch of "Classical Mechanics", in order to get into Bernoulli’s Equation.
So, without further ado, let's dive straight into it!
Energy Conservation and Flow
In order to satisfy flow continuity the velocity of ideal fluid (uncompressed fluid with no viscosity) changes along the path it flows. A narrower path means higher velocity, which in turn yields an increase in kinetic energy. What is constant in any case is the flow rate.
So, where does that energy come from? Energy conservation comes into mind. The energy must come from work done by some force that acts upon the fluid. Its possible to express this using the work-energy principle:
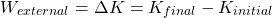
Let's simplify this analysis even further by considering only friction-less laminar flow, with no energy loss due to dissipative forces.
Of course, no external force is applied upon the system, which means that the force must come from some portion of the fluid itself. The work is thus done by pressure from surrounding fluid. This pressure exerts force that does work and causes the fluid to speed up.

So, as the net work done by the pressure increases the fluid's kinetic energy, the pressure of the fluid drops. The pressure is thus different in different regions of the fluid, as otherwise the net force would be zero. As the fluid accelerates it always moves from a higher-pressure region to a lower-pressure region.
Lastly, we should also not forget that pressure in fluid is affected by the height or depth of it. The difference in height causes an additional pressure, which is completely unrelated to the flow speed. It's related to the conservative force of gravity.
All this leads to a very useful relationship between the pressure, the flow speed and the height in a fluid, which is known as Bernoulli's equation.
Bernoulli’s Equation
In order to end up with Bernoulli's equation, we will apply the work-energy theorem at some portion of a fluid pipe. Consider a fluid pipe with varying diameter and height as shown below.
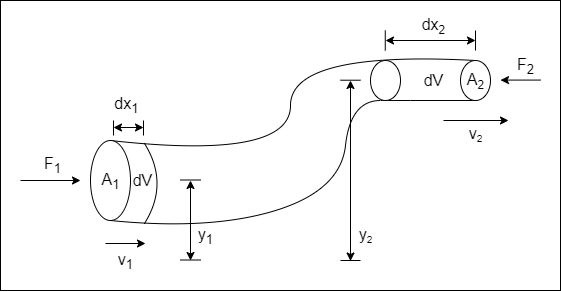
During a period of time dt the same volume of fluid dV flows through any given section of the fluid pipe. So, the sections with cross-section A1 and cross-section A2 respectively are related as follows:

The total work done during that same period of time due to pressure and in turn the forces F1 and F2 can be expressed as:
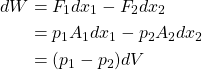
The work done is also equal to the change in kinetic and potential energy. The change in kinetic energy can be expressed as follows:
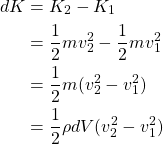
The corresponding potential energy is:

Combining these equations, the total work is:

Rearranging the equation gives us Bernoulli's equation:
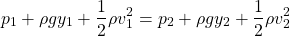
or
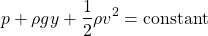
Static Fluids
For static fluids (v1 = v2 = 0) and a reference height of h2 = 0:
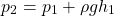
which yet again shows that pressure increases with depth.
Constant Depth
Another common situation is constant depth, h1 = h2. In that case only the pressure and velocity are now present. It's common to call this form of the equation Bernoulli's principle:
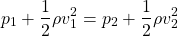
It has lots of applications that we will cover in the examples post.
RESOURCES:
References
- https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/14-6-bernoullis-equation/
- https://www.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is-bernoullis-equation
Images
Mathematical equations used in this article, where made using quicklatex.
Visualizations were made using draw.io.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
- Angular Momentum -> Angular Momentum and its conservation
- Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
- Exercises around Angular motion -> Angular motion examples
Equilibrium and Elasticity
- Rigid Body Equilibrium -> Equilibrium Conditions of Rigid Bodies, Center of Gravity, Solving Equilibrium Problems
- Force Couple System -> Force Couple System, Example
- Tensile Stress and Strain -> Tensile Stress, Tensile Strain, Young's Modulus, Poisson's Ratio
- Volumetric Stress and Strain -> Volumetric Stress, Volumetric Strain, Bulk's Modulus of Elasticity, Compressibility
- Cross-Sectional Stress and Strain -> Shear Stress, Shear Strain, Shear Modulus
- Elasticity and Plasticity of Common Materials -> Elasticity, Plasticity, Stress-Strain Diagram, Fracture, Common Materials
- Rigid Body Equilibrium Exercises -> Center of Gravity Calculation, Equilibrium Problems
- Exercises on Elasticity and Plasticity -> Young Modulus, Bulk Modulus and Shear Modulus Examples
Gravity
- Newton's Law of Gravitation -> Newton's Law of Gravity, Gravitational Constant G
- Weight: The Force of Gravity -> Weight, Gravitational Acceleration, Gravity on Earth and Planets of the Solar System
- Gravitational Fields -> Gravitational Field Mathematics and Visualization
- Gravitational Potential Energy -> Gravitational Potential Energy, Potential and Escape Velocity
- Exercises around Newtonian Gravity (part 1) -> Examples on the Universal Law of Gravitation
- Exercises around Newtonian Gravity (part2) -> Examples on Gravitational Fields and Potential Energy
- Explaining the Physics behind Satellite Motion -> The Circular Motion of Satellites
- Kepler's Laws of Planetary Motion -> Kepler's Story, Elliptical Orbits, Kepler's Laws
- Spherical Mass Distributions -> Spherical Mass Distribution, Gravity Outside and Within a Spherical Shell, Simple Examples
- Earth's Rotation and its Effect on Gravity -> Gravity on Earth, Apparent Weight
- Black Holes and Schwarzschild Radius -> Black Holes (Creation, Types, How To "See" Them), Schwarzschild Radius
Periodic Motion
- Periodic Motion Fundamentals -> Fundamentals (Period, Frequency, Angular Frequency, Return Force, Acceleration, Velocity, Amplitude), Simple Harmonic Motion, Example
- Energy in Simple Harmonic Motion -> Forms of Energy in SHM (Potential, Kinetic, Total and Maximum Energy, Maximum Velocity), Simple Example
- Simple Harmonic Motion Equations -> SHM Equations (Displacement, Velocity, Acceleration, Phase Angle, Amplitude)
- Simple Harmonic Motion and Reference Circle -> SHM and Smooth Circular Motion, Reference Circle
- Simple Harmonic Motion Exercises -> 2 Complete Examples on Simple Harmonic Motion
- Simple Pendulum -> Simple Pendulum (Return Force, Small Angle Approximations, More Accurate Period, Gravity Approximation)
- Physical Pendulum -> Physical Pendulum (Return Torque, Small Angle Approximations, Estimating Moment of Inertia)
- Exercises around Pendulums -> Complete Examples on the 2 types of Pendulums (Simple, Physical)
- Damped Oscillation -> Damping Force, Total Force and Differential Equation, Motion Equations, Special Cases
- Forced Oscillation and Resonance -> Forced Oscillation (Differential Equation, Amplitude, Resonance)
- Exercises around Damped and Forced Oscillation -> Complete Examples on Damped Oscillation and Forced Oscillation
- Chaos and Chaotic Oscillation -> Chaos, Unpredictability and Randomness, Chaotic Oscillation
Fluid Mechanics
- Density and Pressure -> Fluids and Fluid Mechanics, Density, Specific Gravity, Pressure
- Measuring Pressure in Fluids -> Pressure in Fluids (Variation with Depth), Absolute and Gauge Pressure, Measuring Pressure
- Pascal's Principle and Hydraulics -> Static Equilibrium, Pascal's Principle, Hydraulic Systems
- Archimedes' Principle and Buoyancy -> Buoyant Force, Archimedes' Principle, Relation with Density
- Surface Tension -> Surface Tension (Cohesive and Adhesive Forces, Unit, Definition), Capillarity
- Exercises on Fluid Statics (part 1) -> Various Density and Pressure Examples
- Exercises on Fluid Statics (part 2) -> Hydraulic Car Jack, Buoyancy Examples, Surface Tension Example
- Introduction to Fluid Dynamics -> Ideal Fluid, Flow Characteristics, Volume Flow Rate, Flow Continuity, Mass Flow Rate
Final words | Next up
And this is actually it for today's post!
Next time we will talk about Viscosity and Turbulence...
See ya!

Keep on drifting!
Posted with STEMGeeks
I never learned this in school 🤣 Thanks to you guys Stemgeeks I will have the chance to learn.
!1UP
You have received a 1UP from @ivarbjorn!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.