Mathematics - Discrete Mathematics - Sets and Relations

[Image 1]

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Sets and Relations.

So, without further ado, let's get straight into it!

---

Cartesian Product of Sets

The Cartesian Product of two non-empty sets A and B (in that order), denoted by A x B, is the set of all ordered pairs, where the first member belongs to set A and the second member belongs to set B.

In set builder notation:

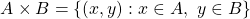
(Binary) Relation

Each subset of A x B is called a (binary) relation R from set A to B. As such, if (x, y) ∈ R and R ⊆ A x B then x is related to y by R. If A = B then R ⊆ A x A is known as a relation on A.

Function

A relation R is called a function when there's exactly one output for each input. In other words, there have to be no ordered pairs with the same first member and different second member.

Example

For example, if A = {1, 3, 5} and B = {2, 4, 6} then the following would be valid relations for the cartesian product A x B:

• R₁ = { (1, 2), (1, 4), (3, 2), (3, 6), (5, 4) }
• R₂ = { (1, 4), (1, 6), (3, 4), (5, 2) }
• R₃ = { (1, 2), (3, 6), (5, 2) }

Only the last one is also a function!

---

Relation Terminology

A relation is commonly denoted as R : A → B.

Domain and Range

The set of all first members in the ordered pairs of R (the inputs) is known as the domain of relation, and commonly denoted by DOM (R).

The set of all second members in the ordered pairs of R (the outputs) is known as the range of the definition, and commonly denoted by RAN (R).

As such, if R : D → S, D would be the domain of definition and S the range of the relation.

Types and Properties

Relations are classified into types depending on the properties they satisfy.

A relation R on set A is:

• Reflexive : (x, x) ∈ R for every x ∈ A
• Irreflexive : (x, x) ∉ R for every x ∈ A
• Symmetric : (x, y) ∈ R ⟺ (y, x) ∈ R for every x ∈ A, y ∈ A
• Antisymmetric : (x, y) ∈ R ⟺ (y, x) ∈ R only when x = y
• Asymmetric : (x, y) ∈ R ⟺ (y, x) ∉ R for every x ∈ A, y ∈ A
• Transitive : (x, y) ∈ R and (y, z) ∈ R ⟺ (x, z) ∈ R
• Identity or Equivalence: Reflexive, Symmetric and Transitive
• Partial Order : Reflexive, Antisymmetric and Transitive

Example

Consider the set A = { 1, 2, 3 }.

Valid relations of the form R : A → A are:

• R₁ = { (1, 1), (2, 2), (3, 3) }, which is reflexive
• R₂ = { (1, 2), (1, 3), (2, 1), (3, 1) }, which is symmetric

---

Function Terminology

A function is commonly denoted as f : A → B.

Domain, Co-Domain and Range

Each element from set A is uniquely associated to an element in set B. The set A is called the Domain of the function, whilst the set B is called the Co-Domain of the function. The range of a function is the image of the domain, and thus a subset of the co-domain.

Types and Properties

Functions are classified into types depending on properties they satisfy.

As such, a function f is:

• Injective : Each element of the Domain set is connected to an element of the Co-Domain Set
• Surjective : Each element of the Co-Domain set has a pre-image from the Domain Set (the co-domain and range are equal)
• Bijective : Both Injective and Surjective

The set cardinalities will be related in the following way:

• Injective : |A| ≤ |B|
• Surjective : |A| ≥ |B|
• Bijective : |A| = |B|

Example

Consider f : Z → N, f(x) = 2x + 1.

The function is injective but not surjective, because:

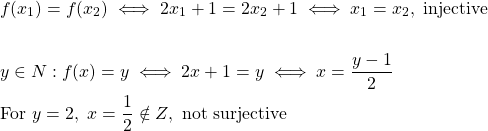
So, the range of function f is not the co-domain N but a subset of N.

---

RESOURCES:

References

1. https://www.javatpoint.com/discrete-mathematics-tutorial
2. http://discrete.openmathbooks.org/dmoi3.html
3. https://brilliant.org/wiki/discrete-mathematics/

Images

1. https://commons.wikimedia.org/wiki/File:Kern_Mathematik.svg

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

---

Previous articles of the series

• Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
• Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
• Set Operations → Venn Diagrams, Set Operations, Properties and Laws

---

Final words | Next up

And this is actually it for today's post!

Next time we will continue on with more on Relations...

See ya!

Keep on drifting!

Posted with STEMGeeks