Mathematics - Discrete Mathematics - Probability

[Image 1]

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Probability.

So, without further ado, let's get straight into it!

Probability Theory

Probability theory is the branch of mathematics concerned with the probability of events from occurring. Based on probability, it's possible to predict the future outcome of an event with a certain probability of being correct, but in general the outcome of such trials is always uncertain.

In the context of computer science, probability is very useful when analyzing the complexity of algorithms.

Probability

Consider an event A. The probability of event A from happening is denoted as P(A). Probability has a value in the closed range [0, 1], where:

• 1 : certain event
• 0 : impossible event

Of course, the probability of an event from happening and not happening (complement event) always adds up to 1:

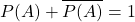
Let's now consider a probability experiment. The set of all possible outcomes of that experiment is referred to as the sample space. In that context, an event is basically a subset of the sample space. So, if S is the sample space set and E the subset of the outcomes in favor of an event A, the probability of P(A) can be written as:

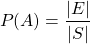
This equation only applies if all outcomes are equally likely to happen. Such sample spaces are basically uniform. For example, tossing a coin or rolling a dice falls into that category.

Theorems

Before getting into the addition and multiplication theorems, let's first mention some more terms related to probability...

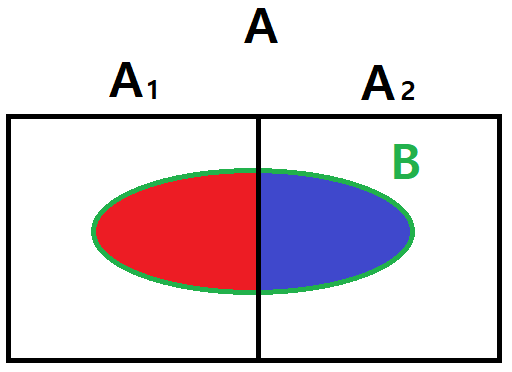
Being defined by sets, events can be easily related to each other by using Venn diagrams and algebra from Set Theory. As such, two events which cannot occur simultaneously are basically mutually exclusive or disjoint events. Their intersection equals the empty set:

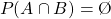
Addition Theorem

For disjoint events, the probability of the union equals the sum of the individual probabilities:

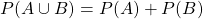
If the events aren't disjoint then the intersection needs to be excluded:

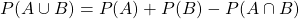
Multiplication Theorem

For independent events, the probability of both occurring at the same time equals the product of their individual probabilities:

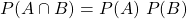
Example

Consider the probability experiment of tossing a dice.

The sample space is of course S = {1, 2, 3, 4, 5, 6}.

Supposing the following events:

• E = {2, 4, 6} : tossing an even number
• O = {1, 3, 5} : tossing an odd number
• A = {3, 4}
• B = {5, 6}

let's calculate the following probabilities:

• P(E)
• P(A)
• P(E ∪ O)
• P(E ∪ A)

The probabilities of the first two events are simply:

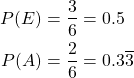
The union of the E and O events results in the sample space S, which is a certain event, and so the probability is 1.

For the union of the two non-disjoint events E and A, the intersection needs to be considered as well. The intersection is the set {4}, and so the probability is:

RESOURCES:

References

1. https://www.javatpoint.com/discrete-mathematics-tutorial
2. http://discrete.openmathbooks.org/dmoi3.html
3. https://brilliant.org/wiki/discrete-mathematics/

Images

1. https://commons.wikimedia.org/wiki/File:Law_of_total_probability.png

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

• Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
• Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
• Set Operations → Venn Diagrams, Set Operations, Properties and Laws
• Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
• Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
• Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
• Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
• Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
• Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
• Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
• Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
• Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
• Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
• Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
• Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations

Final words | Next up

And this is actually it for today's post!

Next time we will get into Conditional Probability...

See ya!

Keep on drifting!

Posted with STEMGeeks