Mathematics - Discrete Mathematics - Partial Order Relations and Sets
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Partial Order Relations and Sets.
So, without further ado, let's get straight into it!
Partial Order Relations
A relation R on set A is a partial order relation if it satisfies all three of the following properties:
- Reflexive : (x, x) ∈ R for every x ∈ A
- Antisymmetric : (x, y) ∈ R ⟺ (y, x) ∈ R only when x = y
- Transitive : (x, y) ∈ R and (y, z) ∈ R ⟺ (x, z) ∈ R
Example
A great example of a partial order relation is the subset relation ⊆, since it satisfies all properties:
- A ⊆ A for any set A ⟺ reflexive
- A ⊆ B and B ⊆ A then A = B ⟺ antisymmetric
- A ⊆ B and B ⊆ C then A ⊆ C ⟺ transitive
Partial Order Set (POSET)
The set A together with a partial order relation R on it, commonly denoted by (A, R), is called a partial order set or POSET.
POSET Elements
The members of set A are elements of the partial order set.
Two elements a and b of a set partial order set A are comparable if a ≤ b or b ≤ a via a partial order relation. Otherwise, they are non-comparable.
Max and Min Elements
An element a ∈ A is a maximal element of A if for any other element c ∈ A, c ≤ a.
In a similar manner, an element b ∈ A is a minimal element if for any other element c ∈ A, b ≤ c.
Only one of each can be defined for every POSET.
Upper and Lower Bounds
Consider a subset B of a partial order set A.
Then, a ∈ A is an upper bound of B if c ≤ a for every c ∈ B.
Similarly, b ∈ A is an lower bound of B if b ≤ c for every c ∈ B.
The least upper bound is known as the supremum of B and denoted by Sup(B), whilst the greatest lower bound is known as the infimum of A and denoted by Inf(B).
Hasse Diagrams
Partial Order Relations and Sets are commonly visualized using Hasse diagrams, which are basically ordering diagrams. They are easier to draw then directed graphs, but can be converted back to directed graphs with relative ease.
In a Hasse diagram:
- the individual elements are denoted by points rather than circles
- since partial order is reflexive the connections / edges from each element / vertex to itself are not drawn
- since partial order is transitive implied edges are also skipped
- directional arrows are omitted as the direction of the relation is implied from top-to-bottom
Example
Consider the following Hasse diagram:
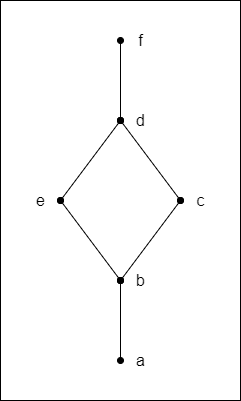
If B = {a, b, e} ⊆ A = {a, b, c, d, e, f} related by the partial order relation R denoted in the Hasse Diagram then:
- a is a minimal as well as the infimum (greatest lower bound)
- e is a maximal as well as the supremum (least upper bound)
- e, d and f are all upper bounds, whilst a is a lower bound.
Total Order Relations
If for all a, b ∈ A of a set A only (a, b) ∈ R or (b, a) ∈ R or a = b then the relation R is a total order relation. Such a relation basically forms a chain.
The total order set is generally a subset of a partially ordered set.
Example
An example of such a relation is '<' on the set of natural numbers N or set of integers Z. Additionally, the '<' relation also doesn't satisfy the reflexive property, and so it can't be classified as an equivalence relation nor a partial order relation.
Lattices
There is a Lattice in a POSET if for any pair of members there is a least upper bound and a greatest lower bound.
Lattices have properties that make them useful for lots of applications of Computer Science. One of them is Boolean Algebra, as any Boolean Algebra is basically a Lattice.
There might be a dedicated post on them later on...
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
Final words | Next up
And this is actually it for today's post!
Next time we will start with a new concept, either Combinatorics or Propositional Logic...
See ya!

Keep on drifting!
Posted with STEMGeeks