Mathematics - Discrete Mathematics - Graphs 2

over 2 years ago

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Graphs 2.

As always, I highly suggest checking out the previous part before this one...

So, without further ado, let's get straight into it!

Graph Representation

There are two main ways of representing graphs:

adjacency matrix
adjacency lists

Let's get into each one separately...

Adjacency Matrix

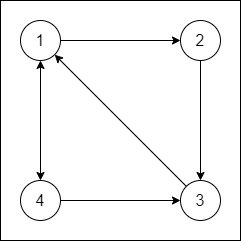
If G is a graph with n vertices, then the adjacency matrix is an n x n matrix A, where each element a_ij is defined as:

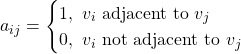
As such if there's an edge between vertices v_i and v_j there will be a 1 in the corresponding row-column pair of the matrix. Similarly, when there's no edge there will be a 0.

In the case of a directed graph the number of 1's equals the number of edges.

For multigraphs the 1 is replaced by the number of edges between the respective vertices.

Adjacency Lists

If G is a graph with n vertices then the corresponding n adjacency lists, one for each vertex, contain the vertices each vertex is adjacent to.

Such a representation can be used for both directed and undirected graphs, but not for multigraphs.

Example

Let's consider the following directed graph:

The corresponding adjacency matrix is:

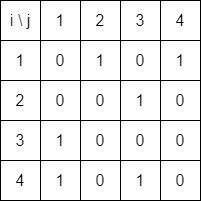
whilst the respective adjacency lists are:

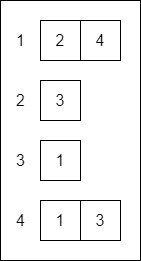
Graph Types and Properties

In addition to the types and properties mentioned last time, there are even more which are worth mentioning.

Isomorphic Graphs

Graphs are isomorphic if they are the same. Isomorphism is thus the analogy of equality in the context of graphs.

Of course, due to their nature it's possible to visualize graphs in various ways, different names in the vertices etc. So, graphs are basically isomorphic when it's possible to relate all edges 1-to-1.

For graphs G₁ and G₂ an isomorphism is basically a bijection f between the respective vertex sets V₁ and V₂, such that when (a, b) is an edge in G₁ if and only if (f(a), f(b)) is an edge in G₂.

For example the following graphs are isomorphic:

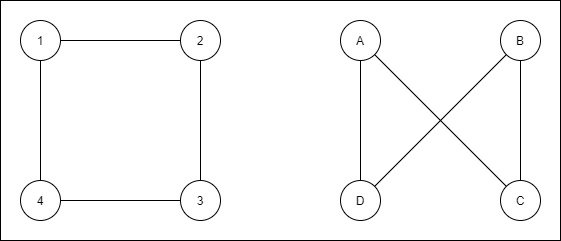
because vertices B and C are basically 3 and 2 respectively.

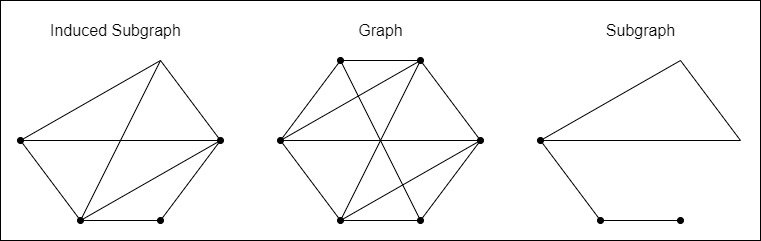
Subgraphs

A subgraph of a graph consists of a subset of the vertices and edges of the "parent" graph. Therefore, if G = (V, E) and G' = (V', E') is a subgraph then V' ⊆ V and E' ⊆ E.

One special case is the induced subgraph, where every edge of E whose vertices are still in V' is an edge in E'. So, in order to create an induced subgraph some vertices and only their adjacent edges are removed.

Lastly, when removing only edges but keeping the original vertices of G, then the subgraph is a so called spanning subgraph.

For example:

Bipartite Graphs

A graph G whose vertices can be partitioned into two subsets V₁ and V₂, so that each edge connects a vertex from V₁ to a vertex of V₂ is known as a bipartite graph.

For example:

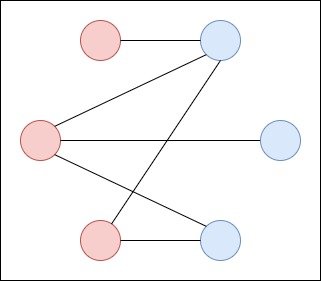
If each vertex of V₁ is connected with an edge to each vertex of V₂ then the graph is a complete bipartite graph.

Regular Graphs

A graph G is regular or more specifically K-regular if all vertices have the same degree K.

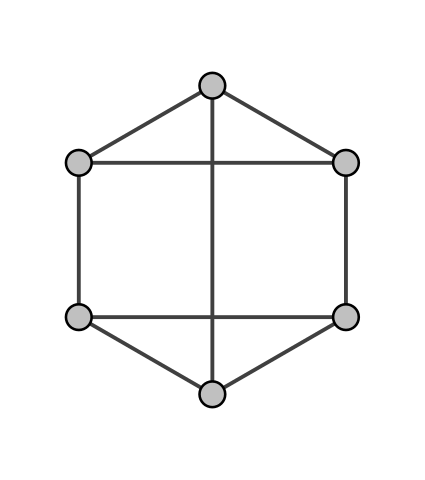
[Image 2]

Planar Graphs

Graphs that can be "drawn" on a flat plane with no edges crossing are called planar graphs.

For such graphs it's possible to define the concept of faces, where faces are basically the regions bound by edges and containing no edges on the interior.

Such graphs, also satisfy Euler's Formula:

where V is the number of vertices, F the number of faces and E the number of edges.

For example:

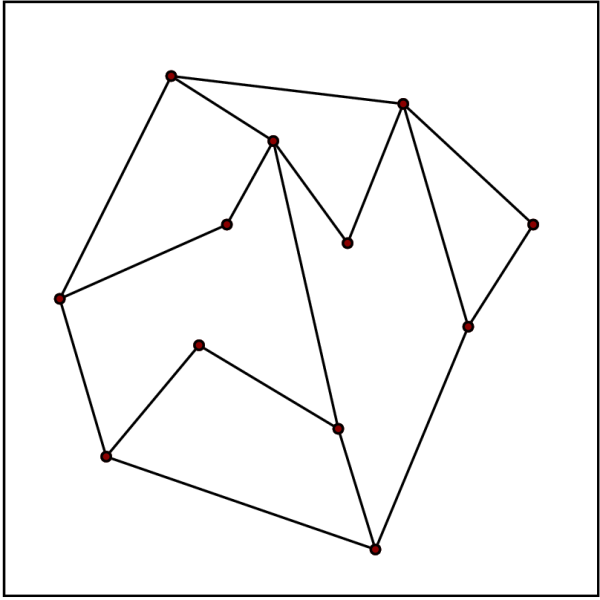
[Image 3]

RESOURCES:

References

Images

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
Set Operations → Venn Diagrams, Set Operations, Properties and Laws
Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
Probability → Probability Theory, Probability, Theorems, Example
Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)