Mathematics - Discrete Mathematics - Conditional Probability

over 2 years ago

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Conditional Probability.

I highly suggest checking the post on Probability before this one!

So, without further ado, let's get straight into it!

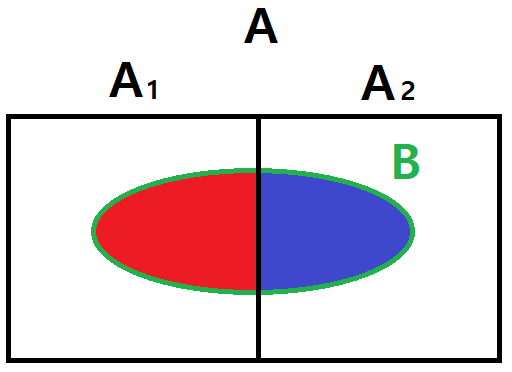
Conditional Probability

For dependent events, where the occurrence of one affects the outcome of another, a new kind of probability is defined known as conditional probability. The probability of an event A from occurring when an event B has already occurred is denoted as P(A | B), and given by:

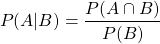
Solving for the intersection, results in:

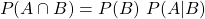
In a similar manner, the probability of event B from occurring when A has occurred is:

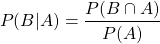
If the events A and B are independent then:

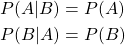
Law of Total Probability

Based on conditional probability, it's possible to calculate the total probability of an event B for any number of disjoint events A_i. The resulting equation is known as the law of total probability:

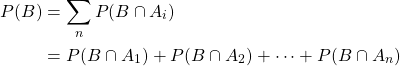
Each intersection can also be replaced with the corresponding conditional probability equation yielding:

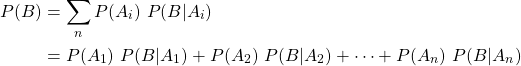
Bayes' Theorem

Let's not forget to mention Bayes' Theorem, which is basically an equation that relates P(A | B) and P(B | A).

It's easy to derive such an equation from the definition of conditional probability:

Note: Of course commutativity applies for the intersection of A and B.

So, knowing P(A), P(B) and either of the two it's possible to calculate the other using this equation.

Full-On Example

Consider a bowl is filled with 3 black and 5 white marbles. What's the probability of picking:

two consecutive black marbles
black marble followed by white marble
three consecutive black marbles
a black marble in the second pick

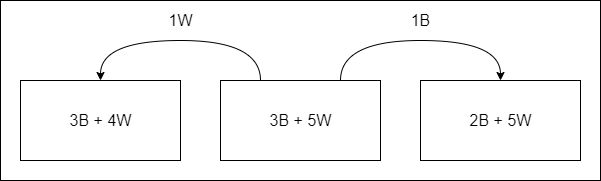
The overall number of marbles is 8, and so the probabilities of picking a black and white marble respectively are initially:

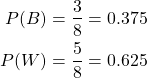
Two consecutive black marbles

After picking a black marble, 7 marbles will be remaining, with only 2 being black. The probability of picking a second black marble, after a black one has already been picked, is thus:

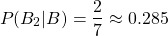
And so, the total probability for picking two consecutive black marbles is:

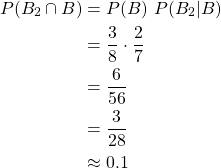
Black marble followed by white marble

After picking a black marble, 5 out of the 7 remaining ones will be white. So, the probability of picking a white one after a black marble is:

As such, the total probability for picking a black marble followed by a white marble is:

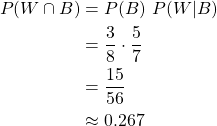
Bonus: Of course, the order doesn't matter in this problem, as picking a white one and then a black one has the same probability (it's simply the intersection of B and W in either order). As such, after picking a white one 3 black marbles will remain, giving the same total probability of:

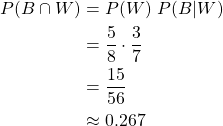
Three consecutive black marbles

After two black marbles have already been picked, picking a third marble has a probability of:

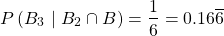
as 6 marbles will remain with only 1 being black.

As such, the total probability is:

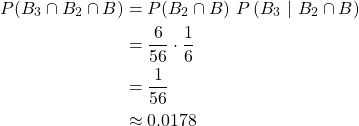
In other words, the probability is basically the product:

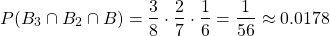
as each pick depends on the previous pick.

Black marble in second pick

This last case is a great example of the law of total probability!

Because it's uncertain what came first, the probability will be a sum of two cases:

black marble was picked first
white marble was picked first

So, picking a black marble in the second pick has a probability of:

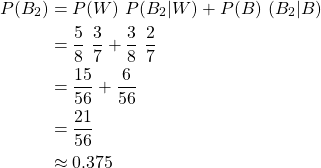
RESOURCES:

References

Images

https://commons.wikimedia.org/wiki/File:Law_of_total_probability.png

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
Set Operations → Venn Diagrams, Set Operations, Properties and Laws
Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
Probability → Probability Theory, Probability, Theorems, Example