Mathematics - Discrete Mathematics - Combinatorics Topics
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Combinatorics Topics.
Combinatorics is basically a branch of Mathematics by itself. Thus, this article will give an overview on some additional topics.
So, without further ado, let's get straight into it!
Pigeonhole Principle
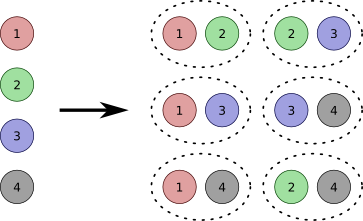
First of all, let's get into the so called Pigeonhole Principle. This principle can be applied for solving a whole variety of problems. The main idea is as follows: if n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
This idea can also be generalized for any natural k, with n pigeonholes being occupied by kn + 1 pigeons, resulting in at least one pigeonhole being occupied by k + 1 or more pigeons.
Example
Let's find the minimum number of students in a class so that at least two of them are born in the same month.
The pigeonholes in this case are the months and so:
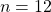
At least two can be translated into:
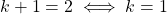
Thus, the minimum number of students is:
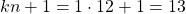
Pascal's Triangle
The values of the binomial coefficient can be visualized in the form of a triangle known as Pascal's Triangle.

[Image 2]
Binomial Theorem
The values of this triangle are also the coefficients of the polynomial expansion of a binomial raised to natural n. The following is known as the binomial theorem (or expansion):
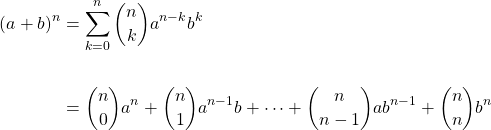
Example
Let's find the coefficient of x 6 in the expansion of (x + 1) 8.
Using the binomial theorem:
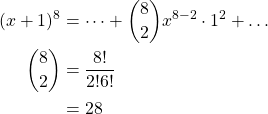
Counting Derangements
Using the inclusion-exclusion principle (PIE) it's possible to solve more advanced counting problems.
One such problem is counting derangements, which is basically the number of permutations where no object is in its original spot in the order.
For example, three numbers have only two derangements. In the context of set {1, 2, 3} these are {2, 3, 1} and {3, 1, 2}.
The procedure of solving such problems is basically as follows: count all permutations and then subtract those that are not derangements.
For any natural n, the number of possible derangements is given by:
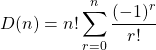
or recursively:
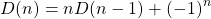
Example
For 4 numbers the number of possible derangements is:
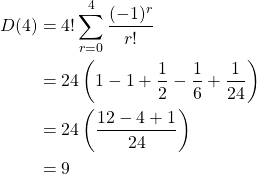
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
- https://commons.wikimedia.org/wiki/File:Combination.png
- https://commons.wikimedia.org/wiki/File:Pascal%27s_triangle_5.svg
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with Propositional Logic...
See ya!

Keep on drifting!
Posted with STEMGeeks