Mathematics - Discrete Mathematics - Combinations and Permutations

over 2 years ago

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Combinations and Permutations.

So, without further ado, let's get straight into it!

Factorial

A n factorial is the product of the n first natural numbers. It is denoted by n!. Additionally, the factorial of 0 is defined as 0! = 1.

Mathematically:

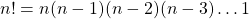
For example:

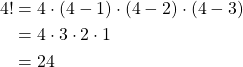
Binomial Coefficient

For any natural number n and k, with 0 ≤ k ≤ n, the following number, known as a binomial coefficient, is defined:

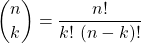
Being read as "n choose k", it can be interpreted as:

the number of ways (combinations) to select k objects from a total of n objects
the number of subsets with cardinality k of a set with cardinality n

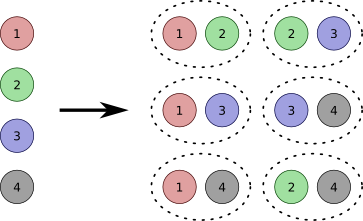
For example, "4 choose 2":

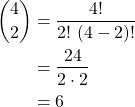
This is also the thumbnail of the post...

Combination

A combination is the selection of some or all objects from a given set of objects, where the order doesn't matter. The number of combinations of n objects, where r are taken at a time is denoted as C(n, r) or n_{c_r}.

The answer to any such problem is the binomial coefficient "n choose r":

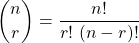
Permutation

A permutation is any arrangement of a set of n objects in a given order. The number of permutations of n things taken all at a time equals n! .

Any arrangement of r objects of a set of n objects in a given order is a r-permutation. It is denoted by P(n, r) or n_{p_r}, and given by:

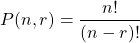
With Repetition

The previous equations are about combinations and permutations, where repeating isn't allowed. With repetition, the result is different.

Permutation

The number of permutations of r objects from n where repetition is allowed is given by n ^r.

For example, 8 bits can be arranged in 2 ⁸ = 256 ways.

Combination

The number of combinations of r objects from n where repetition is allowed is given by:

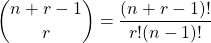
RESOURCES:

References

Images

https://commons.wikimedia.org/wiki/File:Combination.png

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
Set Operations → Venn Diagrams, Set Operations, Properties and Laws
Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)