Mathematics - All About Exponents, Roots and Logarithms

about 3 years ago

Introduction

Hey it's a me again @drifter1!

Today's article is another high-school refresher on Mathematics, and more specifically on Exponents, Roots and Logarithms.

So, without further ado, let's get straight into it!

Exponents

Exponents, which are also known as Powers, specify how many times a base number should be used in a multiplication where it occurs many times by itself. In other words, if b is the base number and p the power, then the corresponding multiplication is:

For example:

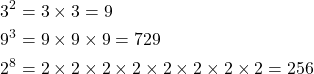
When typing on a keyboard its common to use the ^ symbol. Thus, a^n is the same as aⁿ.

Negative Exponents

If the exponent is negative then it basically specifies how many times we divide by the base number. It might be easier to think of it as fractions of the form 1 by number, which are multiplied by each other.

For example:

From these examples we can see that it is also possible to calculate the positive exponent and simply take the reciprocal afterwards, as shown below.

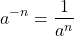
Exponents and Parentheses

Parentheses should be treated with caution (!) as exponents can apply on a single variable or the complete term within parentheses, as shown in the examples below.

The same also applies to minus (-) signs, as the absence of parentheses affects the outcome of exponentiation:

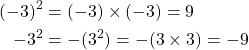
Exponent of 0 and 1

Of course, an exponent of 1 means the number itself:

An exponent of 0 gives a result of 1 for any base except 0. 0⁰ is undefined and requires special handling depending on the problem.

Square and Cube

The square of a number is defined as multiplying it by itself. In terms of exponents it's thus a power of 2.

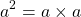
Because multiplying two negative numbers leads to a positive number, the square of any number always gives a positive result! The squares of integers are known as perfect squares.

Similarly, if a number is used three times in a multiplication, we are talking about the cube of that number, or a power of 3.

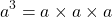
When cubing a negative number the result will now be negative. Cubing natural numbers (>0) yields perfect cubes.

Fractional Exponents (and Roots)

Of course, exponents are not limited to integers. They can be any rational number, and thus even fractions.

In the special case where the exponent is a fraction of the form 1 divided by a natural number, we are talking about a root. For example, 1 / 2 specifies a square root (√) and 1 / 3 a cube root.

In general:

So, what exactly is a root?

The square root is the number which when squared gives the number within the root. For example √9 = 3, because 3 squared equals 9. Similarly, the n-th root is the number which when raised to the power of n yields the number within the root. This is a quite complicated problem! Only perfect squares, cubes etc. are easy to identify or at least simplify.

Complicated fractions like 3 / 2 may look complicated by they are not (!), as they can mostly be translated into simple powers and roots, like a cube (3) and square root (1/2) in that case.

Exponent Properties

The following properties can be used in order to simplify expressions which contain exponents:

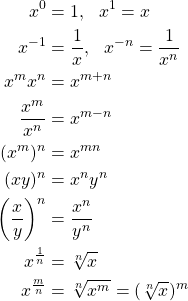
So, remember that:

Multiplying two exponents, m and n, of the same base x, is the same as raising x to a power which is equal to their sum : m + n.
Dividing two exponents, m and n, of the same base x, is equal to raising x to a power which equals the top exponent reduced by the bottom exponent : m - n.
Raising an exponential of a power of m by another exponent n, is equal to raising directly by a power equal to their multiplication : m x n.

Logarithms

With exponents we specify how many times a number is multiplied by itself. With roots we try to find the number which was raised to that power. So, which question remains now?

Well, having a number which is the result of exponentiation, how many times does a given number need to be multiplied by itself in order to end up with that result? What exponent needs to be used? That exactly is a logarithm.

For example:

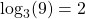
as two 3's are needed in order to end up with 9. The result is basically the required exponent : 3² = 9.

The number which is multiplied is known as the base of the logarithm. The previous example had a base of 3.

Relation of Exponents and Logarithms

It's easy to notice the relationship between exponents and logarithms. Mathematically, it can be defined as:

Common Logarithms

Logarithms written without base are known as common logarithms, and the base is usually 10. So, they specify how many times 10 needs to be multiplied in order to get a desired number.

For example:

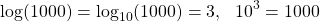
Natural Logarithms

Another commonly used base is Euler's number, e, which is about 2.718. A logarithm with a base of e is known as a natural logarithm and denoted with ln.

Base Change

Changing the base of a logarithm is as simple as dividing by the logarithm of the previous base with a base equal to the new base:

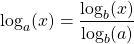
Using the same concept it's also possible to swap x and the base:

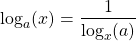
Logarithm Result

Of course, the result of the logarithm can have decimals and be negative as well. A negative logarithm basically specifies how many times we divide by the base number. But, be careful! In log_b(x), x must always be positive. The logarithm of a negative number is undefined!

Also, note that the logarithm of 1 gives us 0 for any base:

Logarithm Properties

Similar properties to those of the exponents can also be defined for logarithms. Those are:

And so remember that:

the logarithm of an multiplication is equal to the sum of the individual logarithms
the logarithm of a division is equal to the difference of the individual logarithms
the logarithm of n to the power of r is equal to r times the logarithm of n