Solving Quadratic Equations With Complex Numbers
Hello there. In this math post, I would like to cover solving quadratic equations with complex numbers. It is assumed that the reader is able to factor and solve quadratic equations and is familiar with the quadratic formula.
As usual, math text (images) rendered with QuickLaTeX.com.
Contents
- Review Of Complex Numbers
- Review Of Exponent Laws
- Solving Quadratics By Taking The Square Root
- Complex Roots From Difference Of Squares Factoring
- Complex Roots From The Quadratic Formula
Review Of Complex Numbers
After the real numbers we have the complex numbers. All complex numbers are real numbers but not all real numbers are complex numbers. The complex number takes on the form of z = a + bi.
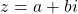
The a represents the real part of the number while the bi part represents the imaginary part of the number. Alongside the coefficient b, the imaginary number i is equal to the square root of negative one.
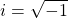
Taking the square of both sides yields the result of i squared being equal to negative one.
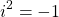
Review Of Exponent Laws
Given two numbers p and q with an exponent n you have the exponent law of:
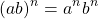
Note that square roots have an exponent of a half. The above exponent law for square roots becomes:
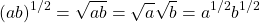
Solving Quadratics By Taking The Square Root
For solving a quadratic equation such as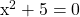 
, you can isolate for the x-squared part.
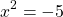
Under the real numbers taking the square root on both sides is bad. With complex numbers you can take the square root on x-squared and on the negative five on the right side.
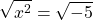
The left side of the above is just x. For the right side negative five can be decomposed into -1 times 5. The square root of negative one is the complex number i and the square root of 5 is left alone.
Complex Roots From Difference Of Squares Factoring
There is the option of applying the difference of squares factoring technique on two term quadratic equations. Let's look at a few examples.
Example One
In the quadratic equation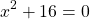 
, you can do difference of squares factoring. The positive 16 has to be rewritten as minus negative 16.
The square root of x-squared is x and the square root of negative 16 is 4i.
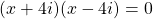
The solutions for this quadratic is plus and minus 4i.
Example Two
Let's look at a tougher quadratic such as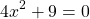 
.
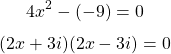
Solving for x in 2x + 3i gives x = -3i/2. The other solution is x = 3i/2.
Complex Roots From The Quadratic Formula
Recall that the quadratic formula is:
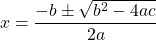
where a, b and c are from the quadratic equation in the form of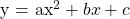 
.
If the discriminant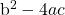 
is negative, you will have a negative inside the square root and have complex roots for the quadratic equation.
Example One
Solve for x in the equation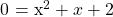 
.
The coefficients for a, b and c are 1, 1 and 2 respectively. Use these values in the quadratic formula.
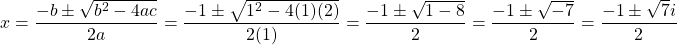
For the plus case you have the answer of 
and the minus case answer would be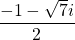 
.
Example Two
In the equation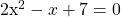 
, solve for x.
The coefficients in this quadratic equation are a = 2, b = -1 and c = 7. Use these values accordingly in the quadratic formula.
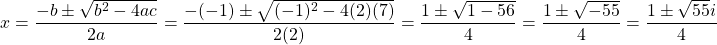
Side Note: The calculator soup website has a nice quadratic formula solver which works with complex numbers.
Posted with STEMGeeks