Reciprocal Trigonometric Ratios [Math]

Hi there. In this math post I cover reciprocal trigonometric ratios. It is assumed that the reader is familiar with sine, cosine and tangent ratios.

Pixabay Image Source

 

Topics

---

• Review Of Sine, Cosine, Tangent Ratios & SOH CAH TOA
• Reciprocal Trig Ratios
• Examples

 

Review Of Sine, Cosine, Tangent Ratios & SOH CAH TOA

---

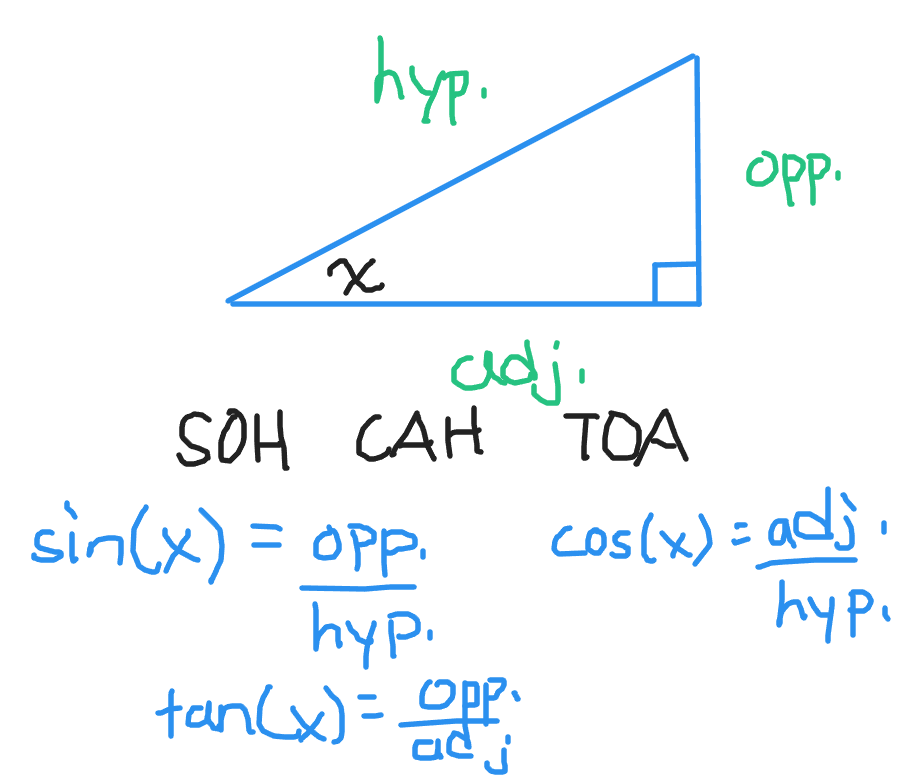
Given a right angle triangle you can obtain trigonometric ratios based on which side lengths and angles are available.

The sine of an angle is the opposite side length divided by the hypotenuse side length.

For the cosine of an angle, it is the adjacent side length divided by the hypotenuse side length.

The tangent of an angle is the opposite side length divided by the adjacent side length.

From the sine, cosine and tangent trigonometric ratios a memory aid called SOH CAH TOA can be formed. It does sound weird but it is a very useful memory aid.

 

Reciprocal Trig Ratios

---

A reciprocal of a fractions is where the fraction is flipped. Flipped is the layman's term of switching the numerator and denominator of a fraction. As an example the reciprocal of 4/7 is 7/4.

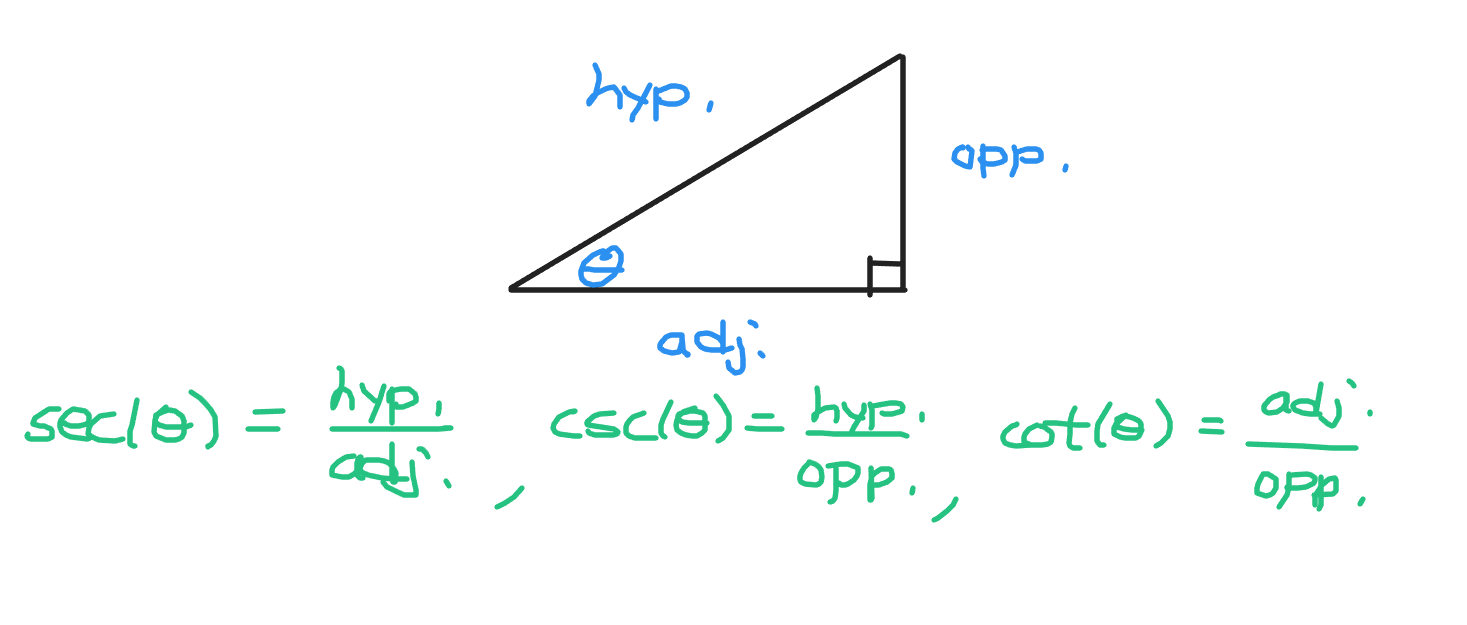
Reciprocal trignometric ratios are based on sine, cosine and tangent trigonometric ratios.

The reciprocal of the sine of an angle is the cosecant of an angle. This is given by csc(x).

For the reciprocal of the cosine of an angle is the secant of an angle. This is given by sec(x).

The cotangent of an angle or cot(x) is the reciprocal of the tangent of an angle.

 

Examples

---

I present examples of obtaining reciprocal trigonometric ratios. Screenshots diagrams are provided here too.

Example One - Cosecant

The cosecant trigonometric function is one divided by the sine function. You can start with the sine trigonometric ratio. After that you can take the reciprocal of the sine fraction by flipping the fraction.

 

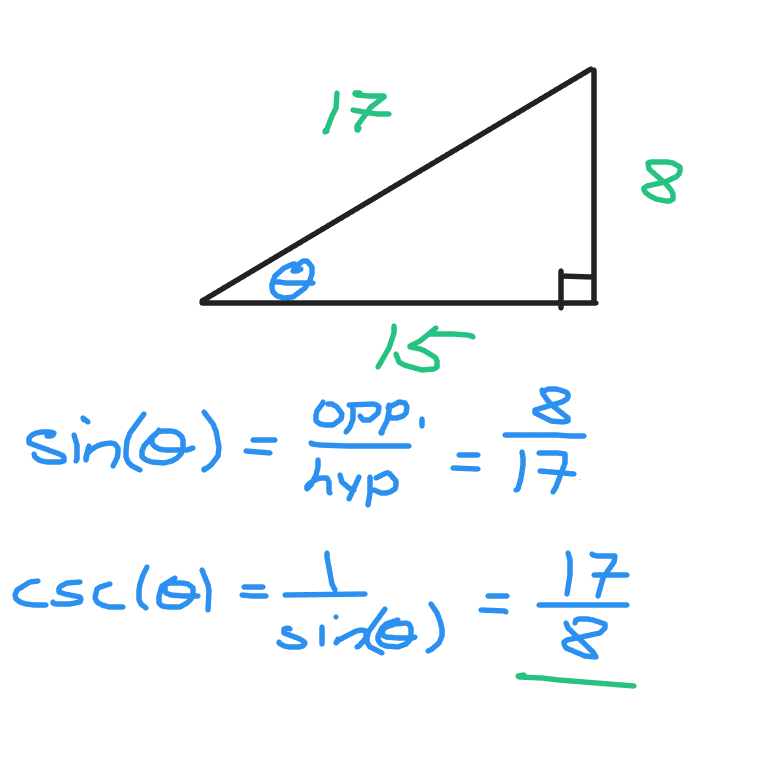
Example Two - Secant

For secant, it is the reciprocal of the cosine function.

 

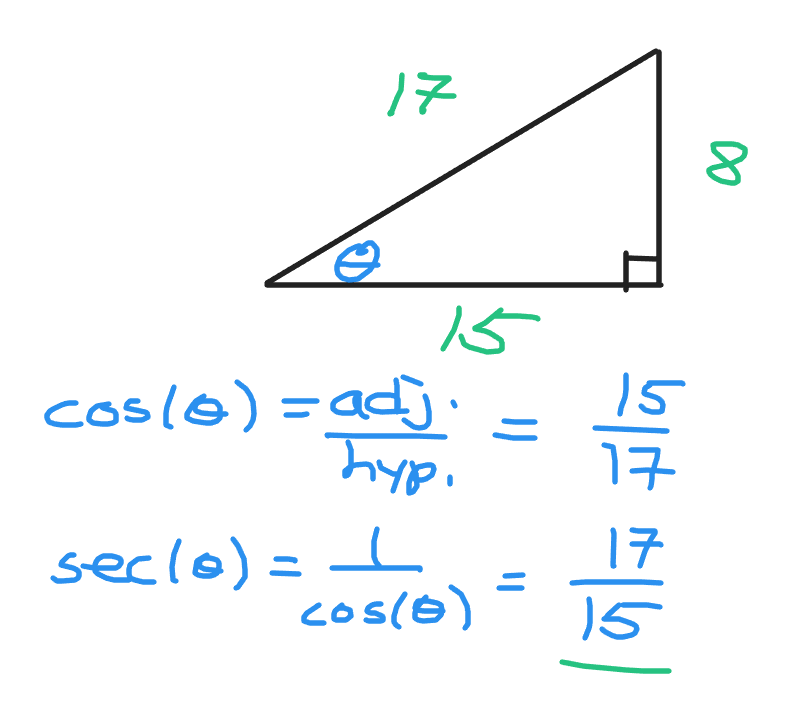
Example Three - Cotangent

Take the reciprocal of the tangent trigonometric ratio to obtain the cotangent trigonometric ratio.

 

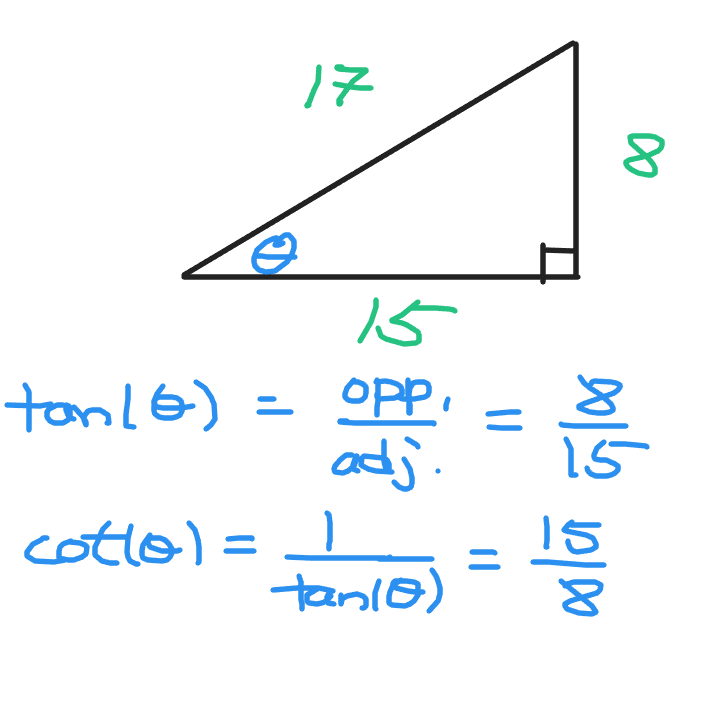
Example Four - Sum Of Trig Ratios

We can obtain the sum of trigonometric ratios through addition, subtraction, multiplication, division and so on. This example deals with the addition of trig ratios.

In this example I add the tangent of the angle theta and the cosine of the angle.

 

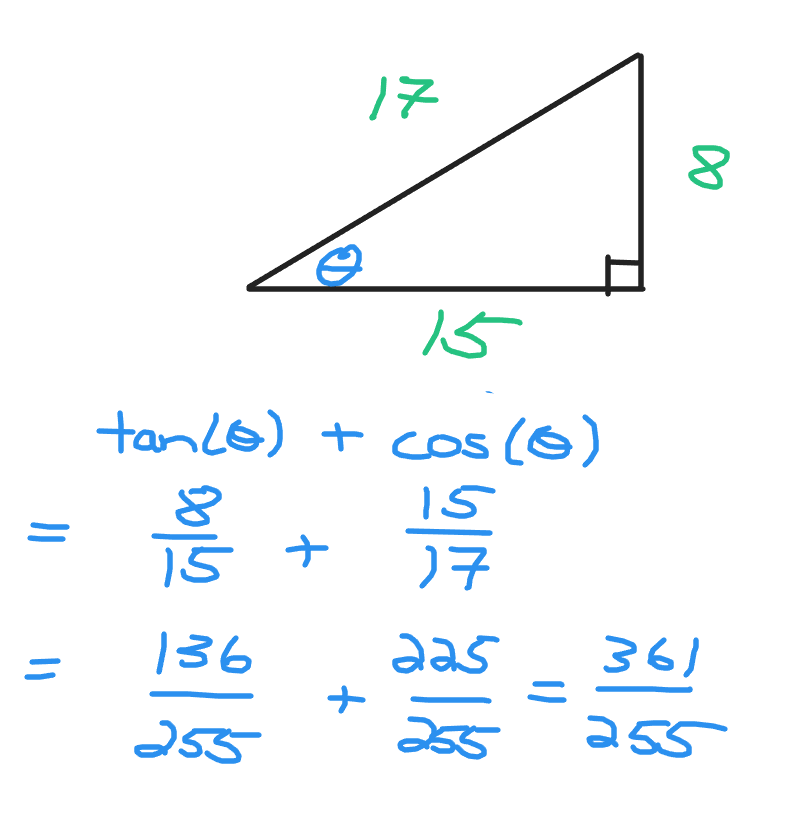
Example Five - Product Of Trig Ratios

With this example, I take the product of two trigonometric ratios. What is the answer to the sine of the angle theta multiplied by the cosine of the angle?

 

Thank you for reading.

Posted with STEMGeeks