Partial Sums Of Arithmetic Series [Math]
Hi there. In this math post, I cover the topic of partial sums of arithmetic series.
This time I mostly use Quicklatex.com and Pixabay for the math images.

Topics
- Arithmetic Sequences Vs Series
- Review Of Arithmetic Sequence Formula
- Understanding The Partial Sums Formula For An Arithmetic Series
- Examples
Arithmetic Sequences Vs Arithmetic Series
In a previous post I covered the concept of arithmetic sequences.
An arithmetic sequence is a list of numbers that add or subtract by the same amount to obtain the next number. One simple example would be 3, 5, 7, 9, 11, 13, 15, 17, ... , 99. This is the odd numbers from 3 to 99 where you add by two to get the next number.
An arithmetic series is like an arithmetic sequence. Instead of listing the numbers, the numbers are added together. Commas are replaced by plus signs. One simple example would be 10 + 15 + 20 + 25 + 30 + 35 + ... + 100. This is adding the numbers from ten to one hundred where the next number is the previous number plus five.

Review Of Arithmetic Sequence Formula
With the arithmetic sequence formula you can obtain any term/number in the sequence. The formula can also be used to obtained the common difference, first number or any number in the sequence.
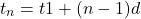
where t_{n} is the n-th number in the sequence, t_{1} is the first number in the sequence and d is the common difference.
Understanding The Partial Sums Formula For An Arithmetic Series
From an arithmetic series, what if you wanted to add some or all of the numbers in the series? Consider a simple arithmetic series of the whole numbers from 1 to 50. That is 1 + 2 + 3 + 4 + 5 + ... + 48 + 49 + 50.
Instead of add from 1 to 50 left to right, consider making pairs in the following way. Add the first number of one and the last number of 50 together to obtain 51 as one pair. The next pair is two and fourty-nine which adds up to 51. The third pair is three and fourty-eight. This can be continued until all numbers are added. The amount of pairs is 25 which is half of 50 and the sum of each pair is 51. Adding the whole numbers from 1 to 50 is the product of 25 and 51. That is 25 pairs where each pair is 51 which is equal to 25 x 51 = 1275.
Witeboard.com screenshot below.
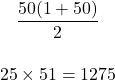
The above was for a specific example. Here is a formula can be used for any arithmetic series.

Divide by two as the number of pairs is the amount of numbers n divided by two. Even if n is odd the formula still works for obtaining the sum of numbers from the first term t1 to the last term tn.
Examples
Example One
What is the total of all the whole positive numbers from 1 to 1000? That is 1 + 2 + 3 + 4 + ... + 1000 = ??
There are one thousand numbers from 1 to 1000. The first number is one and the last number is 1000. Use the partial sum formula with n = 1000 to obtain the total/sum of the whole numbers from 1 to 1000.
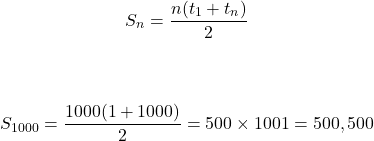
Example Two
Add up all the even numbers from 20 to 140 including 20 and 140.
The first term here is 20 and the last term is 140. As we have even numbers the common difference is two. Note that an even number plus one is an odd number. The next even number would be one after the odd number or even number plus two to get the next even number. It looks like 20, 22, 24, 26, 28, 30, 32, ..., 140.
What we do not have is the number of terms from 20 to 140 inclusive. Use the arithmetic sequence formula and solve for n.

Once the number of terms n in the arithmetic sequence is found we can use the partial sum formula to obtain 20 + 22 + 24 + 26 + ... + 136 + 138 + 140.
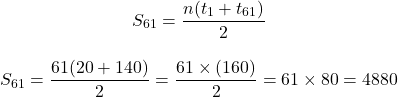
Example Three
Determine the total of -20 + -16 + -12 + -8 + -4 + 0 + 4 + 8 + ... + 204 + 208.
First find the number of terms in the sequence of -20, -16, -12, -8, -4, ..., 204, 208 with the arithmetic sequence formula. Note that the common difference is d = 4 as the next number goes up by 4.

Once the number of terms n is found you can use the partial sum formula to obtain the sum of -20 + -16 + -12 + -8 + -4 + 0 + 4 + 8 + ... + 204 + 208.
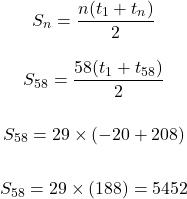

Posted with STEMGeeks
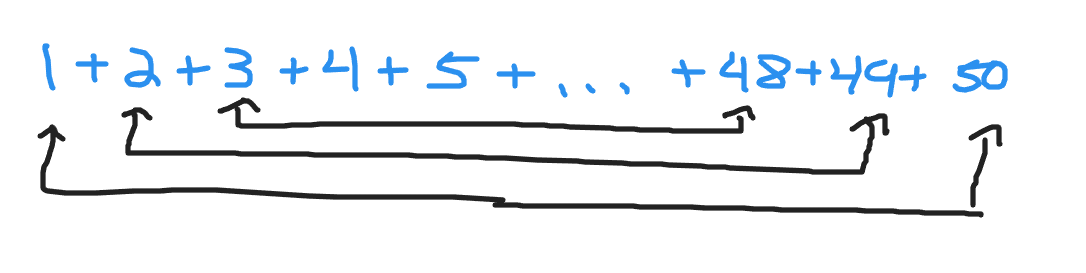
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
I remember doing this in middle school!
!discovery 31
Middle school I see. For me it was high school lol.
This post was shared and voted inside the discord by the curators team of discovery-it
Join our Community and follow our Curation Trail
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program