An Introduction To Trigonometric Ratios & SOH CAH TOA
Hi there. In this math post I provide an introduction to trigonometric ratios of right angled triangles. I also cover the useful memory aid SOH CAH TOA and its usage.
Topics
- Right Angle Triangles
- Trigonometric Ratios - Sine, Cosine, Tangent
- SOH CAH TOA Memory Aid
- Examples
Right Angle Triangles
A right angle triangle is a triangle with one right angle (90 degrees). The other two angles are acute angles with each angle being less than 90 degrees. Note that a triangle with 2 right angles or more is impossible as the sum of the three angles would be more than 180 degrees.
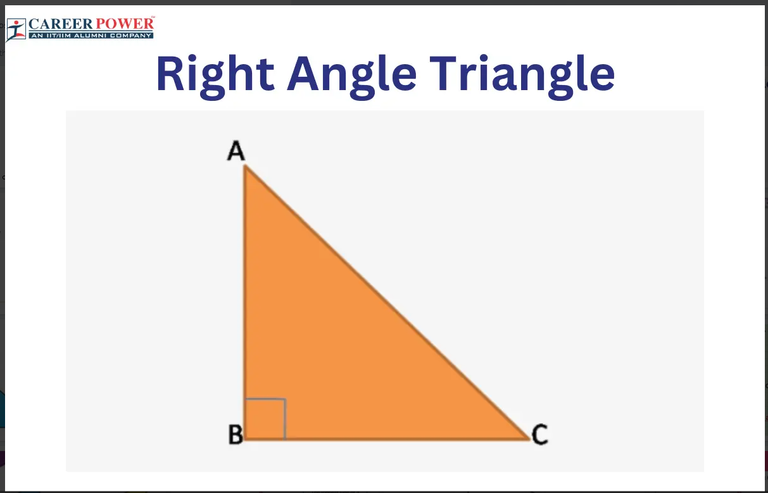
The hypotenuse is the longest side of the right angle triangle. It is always opposite to the right angle. (The right angle is largest angle in the right angled triangle.)
Trigonometric Ratios - Sine, Cosine, Tangent
With trigonometric ratios we can relate an angle of a right angle triangle with the sides.
The sine of an angle is given by the opposite side to the angle divided by the hypotenuse.
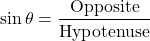
The cosine of the angle θ (theta) is given by the adjacent side to the angle divided by the hypotenuse.
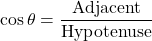
For the tangent, you have the opposite side to the angle divided by the adjacent side length.
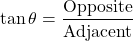
Note that θ (theta) is an angle in the triangle.
Here is a summary image from this site. They use the letter A for the angle referring to the corner at A.
SOH CAH TOA Memory Aid
The ratios for sine, cosine and tangent can be confusing to memorize. A useful memory aid for memorizing the three trigonometric ratios is SOH CAH TOA. How does this work?
For sine you have opposite over hypotenuse. The first letter is sine is S, then you have the letter O in opposite and the letter H in hypotenuse. You get the memory aid SOH for sine.
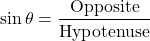
With cosine, you have the letter C from cosine, A from adjacent and H for hypotenuse.
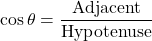
Tangent would be T for tangent, O for opposite and A for adjacent. This gives the TOA memory aid.
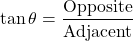
Putting it all together gives you SOH CAH TOA. Summary image below.

Example
Refer to the picture screenshot below for the right angle triangle. I used a combination of witeboard.com and my Wacom tablet.

Here we have the 5-12-13 right triangle. In this example I set up the trigonometric ratios with sine, cosine and tangent. Finding angles is another topic.
Given the angle C in the right angle triangle, we determine the sine, cosine and tangent ratios.
The sine of angle C is opposite over the hypotenuse. The side length opposite to angle C is 5. Thirteen is the hypotenuse. Sine of angle C is 5/13.
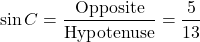
The cosine of angle C is the adjacent side length over the hypotenuse. Twelve is the adjacent side length to angle C. The hypotenuse is 13.
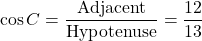
With the tangent of angle C we have the opposite side length over the adjacent side length.
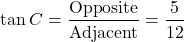

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.