222^333 Or 333^222 - Which Is Bigger ?

I happened to come across this question on a YouTube channel some days ago and it captivated me - basically because I love math. The two operations would actually yield humongous numbers but what's more interesting is that you are required to tell which of the two is bigger without a calculator.

Is 222^333 bigger than 333^222 or is it the other way round ?

However, even if you punch those numbers in a calculator you may still not be able to tell which is bigger. For example, below is what my phone's calculator gave for both operations.

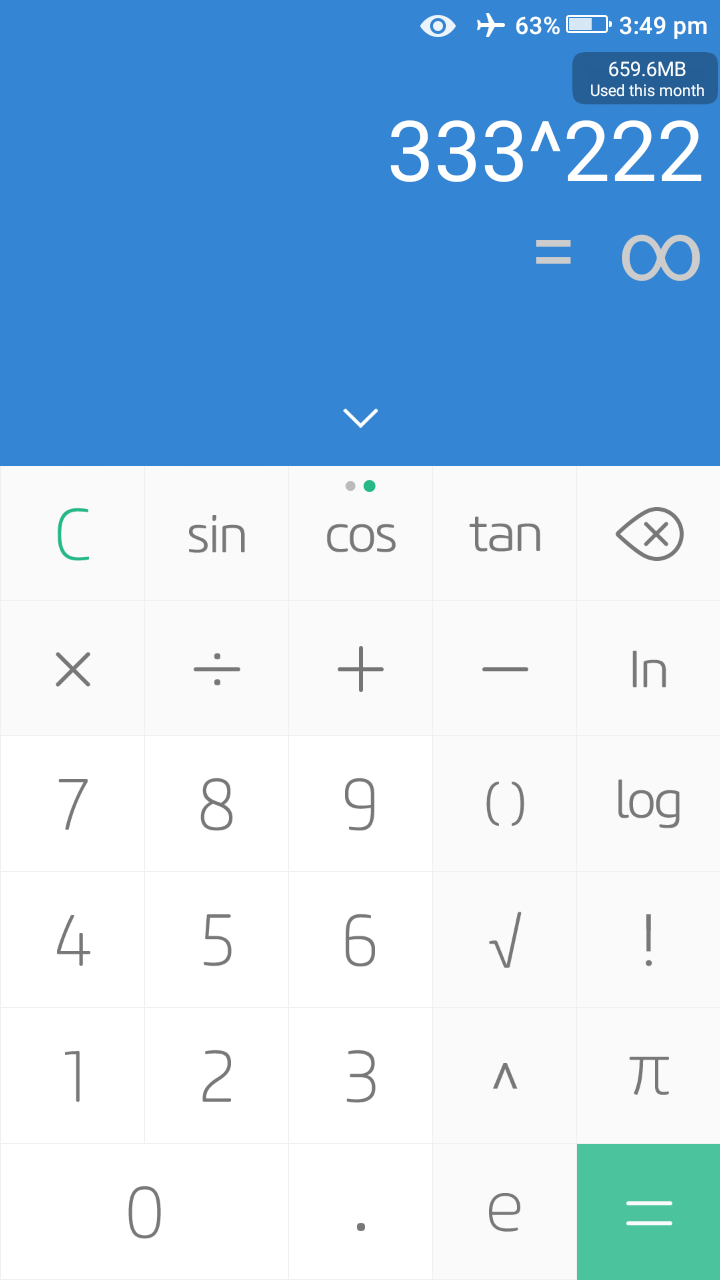
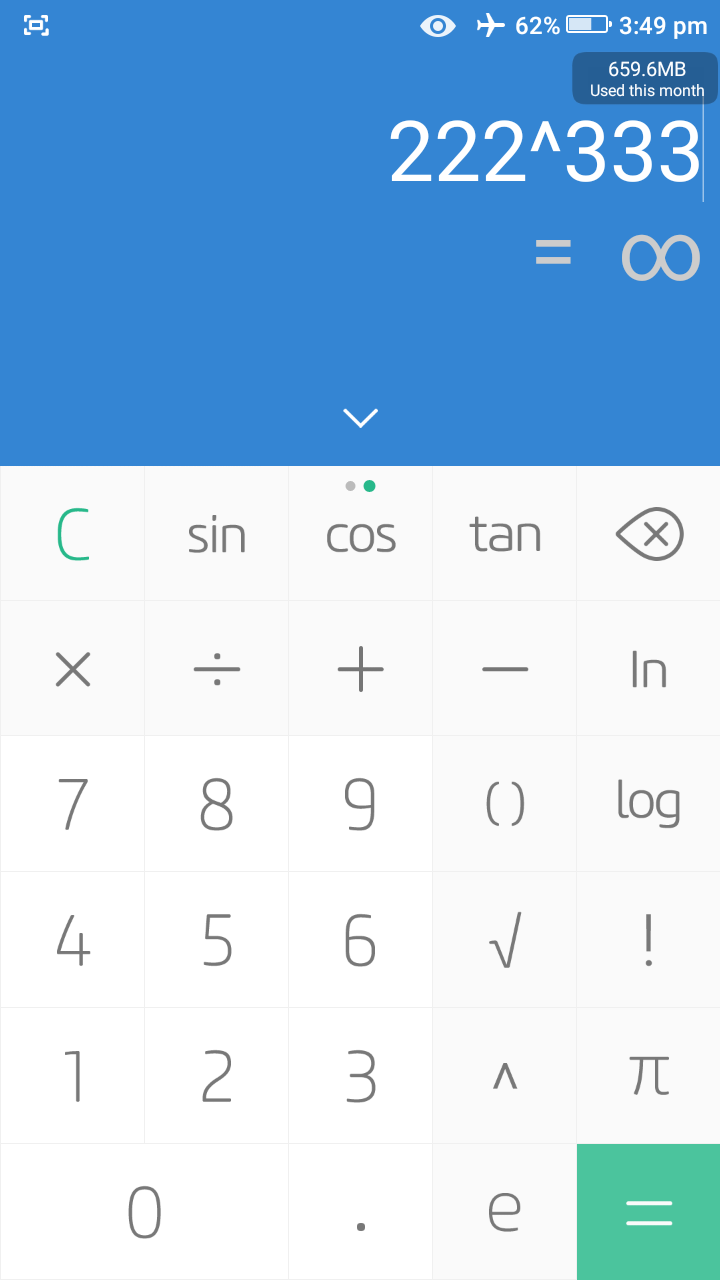
Which means if I wanted to cheat by using my phone's calculator I'll still get fucked up. 😂
Some of us think calculators are better than us, especially in terms of speed but what you don't know is that calculators despite the speed also have limits. One plausible reason why my phone's calculator didn't give me a definitive answer is likely due to memory capacity, it's processing memory can't contain all the numbers - remember i said earlier that those operations would yield humongous numbers. There could be other reasons though.

With the way the question was presented (not involving a calculator), the first thing that comes to mind is that there most be a trick to telling which is bigger without having to know the result of the operations and this is where our brains superiority to calculators comes in.

I however did not play the video to know how they got which was bigger. I sometimes don't search for other people's solutions to certain problems so as make my own discoveries and better understand it. It's been quite a relatively long while since i flexed my mathematical muscle - due to other problems, so it took me long to discover how to answer the question.
So, I'm going to share with us what i discovered.

To non-mathematians, such question looks very intimidating but we can make it less intimidating. In the early 17th century, John Napier discovered something very remarkable that would change mathematics and science for the better. He discovered a function that could simplify complex arithmetic and exponential operations or simplify arithmetic and exponential operations requiring very large numbers, this function is today referred to as the logarithmic function.
If we are going to make those operations look less intimidating, we are going to need the help of the logarithmic function. There are two popular types of logarithmic functions namely, natural logarithm(ln) and common logarithm(Log). For simplicity we would make use of the common logarithm (base 10).

Let A = 222^333 and B = 333^222

Following the rules of logarithm such that log(a^b) = b log(a), we would have

Log(A) = 333Log(222) or 333 × Log(222)

And

Log(B) = 222Log(333) or 222 × Log(333)

Notice that the exponential operations have been transformed into multiplication and now looks less intimidating . 😎

The next step would be to find what Log(222) and Log(333) are which looks also difficult because you would need a logarithm table or a calculator. We have no logarithm table nor a calculator, so how do we proceed further ?

Well, it's not very difficult if you are very familiar with logarithms. The common logarithm of any number usually requires two parts called the "characteristics" and "mantissa". The characteristics usually comes before the decimal point and the mantissa usually comes after the decimal point. The characteristics is easier to get of hand, simply count the number of digits of the number whose logarithm we are looking for and subtract 1 from it.
222 has three digits (the three 2's), the characteristics of 222 is 2 or (3 - 1)
So,
Log(222) = 2.

Notice the point (decimal) after the 2

Applying the same rule to Log(333), we have

Log(333) = 2.

Notice the point (decimal) again after the 2

Also, we would be having

Log(A) = 333 × 2.

And

Log(B) = 222 × 2.

But we aren't done yet and it's because we need to know the numbers after the decimal point (the mantissa). This mantissa part usually requires logarithm table of which we don't have but hope isn't lost, there's another trick.
However, merely looking at Log(A) and Log(B) it would seem that Log(A) is bigger than Log(B), both are sharing the same 2. but 333 is bigger than 222.
How can we be certain that Log(A) is indeed bigger than Log(B) ?

This can be known through what i call a test of strength as we shall now see.

In one decimal place, the mantissa can take on values "only" in the range of 0 to 9, what this implies is that from 2.0 to 2.4 we can approximate it to 2 while from 2.5 to 2.9 we can approximate it to 3. What we have just done is approximate the likely values of Log(333) and Log(222) using their upper and lower limit (3 and 2 respectively).

The next step is to test the strength of 333 and 222 using a permutation/possible operations that we could be presented with, using the above approximations. You can see it as a boxing match with different rounds between 333 and 222.

We can be presented with values of the kind below

Round 1 (First possibility)

Log(A) = 333 × 2 and Log(B) = 222 × 3

Which is bigger or the winner in round 1 ?

It is a tie (no winner) and it's because both of them have same result (666).

Round 2 (second possibility)

Log(A) = 333 × 3 and Log(B) = 222 × 3

Which is bigger or the winner in round 2 ?

It's obviously Log(A) and it's because 999 (333 × 3) is bigger than 666 (222 × 3).

Last Round (Final possibility)

Log(A) = 333 × 2 and Log(B) = 222 × 2

Log(A) wins again, 666 is bigger than 444

Log(A) had 2 wins while Log(B) had zero wins and there's a single draw. What this means is that Log(A) can either be equal to or bigger than Log(B) irrespective of the actual values of Log(333) and Log(222).

However, based only on number of wins, Log(A) is bigger. We can further confirm this with a calculator as seen in the images below, even though it's no longer necessary.

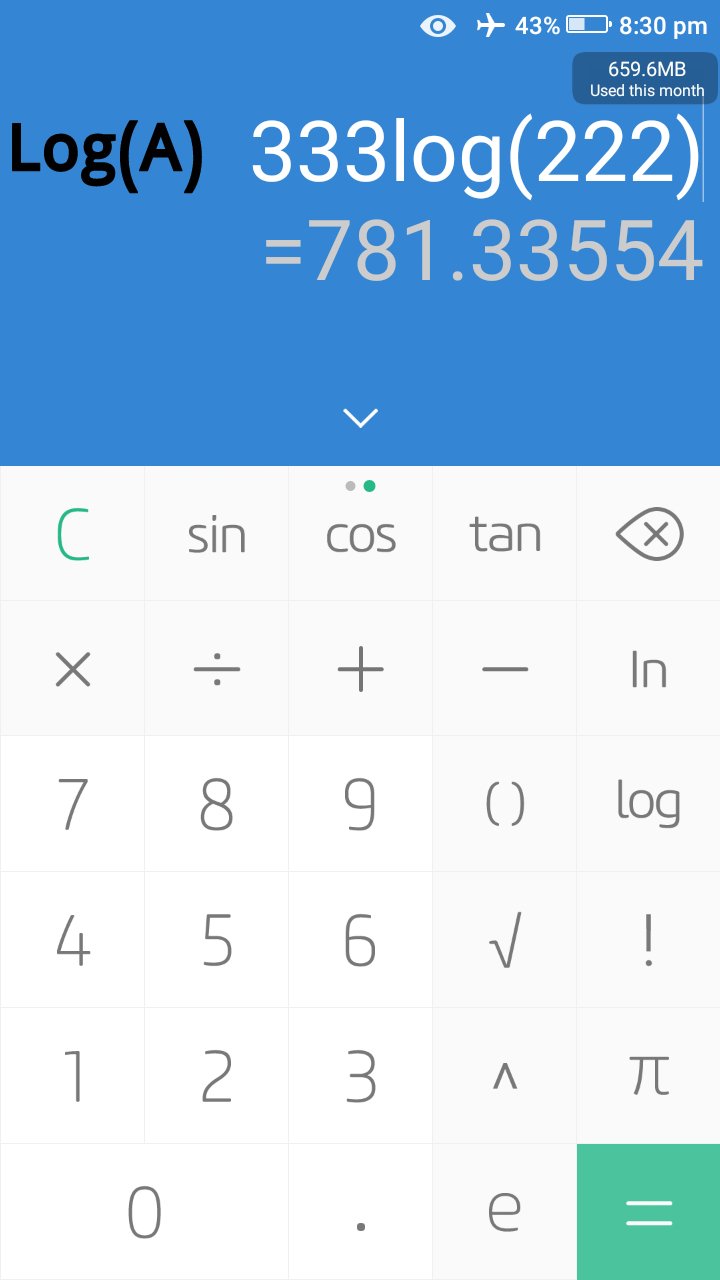
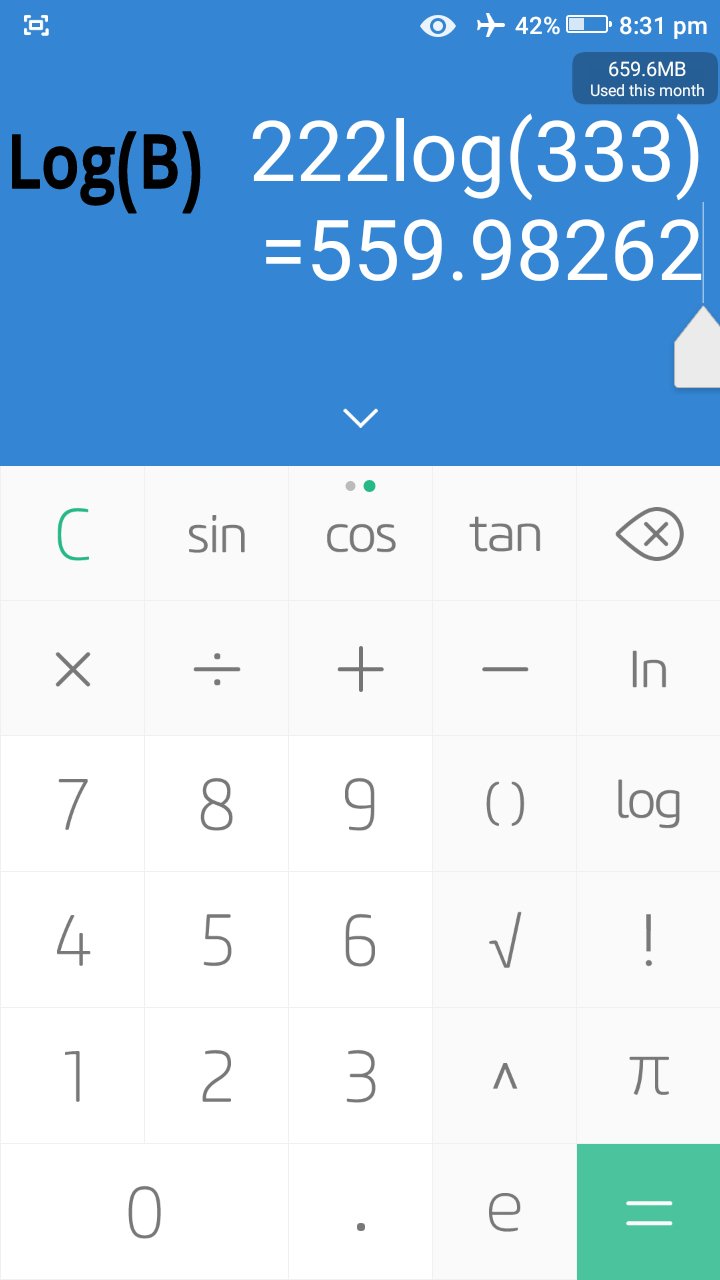
If Log(A) is bigger than Log(B), then A is bigger than B and it means that 222^333 is bigger than 333^222, it's as simple as that.

Math is sweet, you just have to love it. 😉

Thank you all once again for stopping by to read my jargons and also thank you @stemng, @lemouth and the @Steemstem team for your valuable supports.

Source

Lastly, please don't forget to do the needful
Upvote
Comment
Reblog
If you enjoyed my jargons.

Background image source by @doze