Preparation for calculus (Chapter P.I). Exercise 7: Elaborate the graph of the equation by plotting points.

Hello friends and followers of STEM content, this time I want to address a topic that is preparation for calculus, as is the graph of an equation by plotting points.

To do this we are going to place ourselves in chapter P, in the exercises of section P.I on page 8 of the book of calculus with analytic geometry by Larson and Hostetler to solve the proposed exercise number 7 that says:

Plot the graph of the following equation by plotting the following points

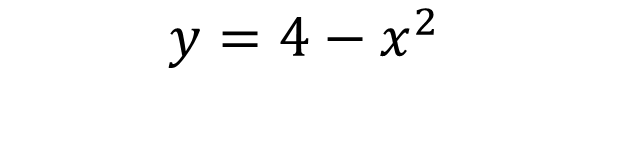
For this purpose, we draw up a table of values:

For x = 0

y = 4-(0)²

y = 4

For x = 1

y = 4 - (1)²

y = 4-1

y = 3

For x = 2

y = 4 - (2)²

y = 4 - 4

y = 0

For x = 3

y = 4 - (3)²

y = 4 - 9

y = -5

For x = 4

y = 4 -(4)²

y = 4-16

y = -12

We fill in the table with the y values:

It is not necessary to find the intersection points, since when x = 0; y = 4. When y = 0; x = 2. The coordinates of these points are the intersections with the Cartesian axes.

The graph is a parabola because the equation is a quadratic function, as follows x² is negative means that the parabola opens downward and the vertex is a maximum point.

The coordinates of the vertex for when the factor BX=0 is the point whose coordinates is the intersection with the X axis, i.e. the vertex has coordinates: (0;4)

The other important thing to keep in mind is that for the same values of x that appear in the table the same values of Y apply but for negative values of x.

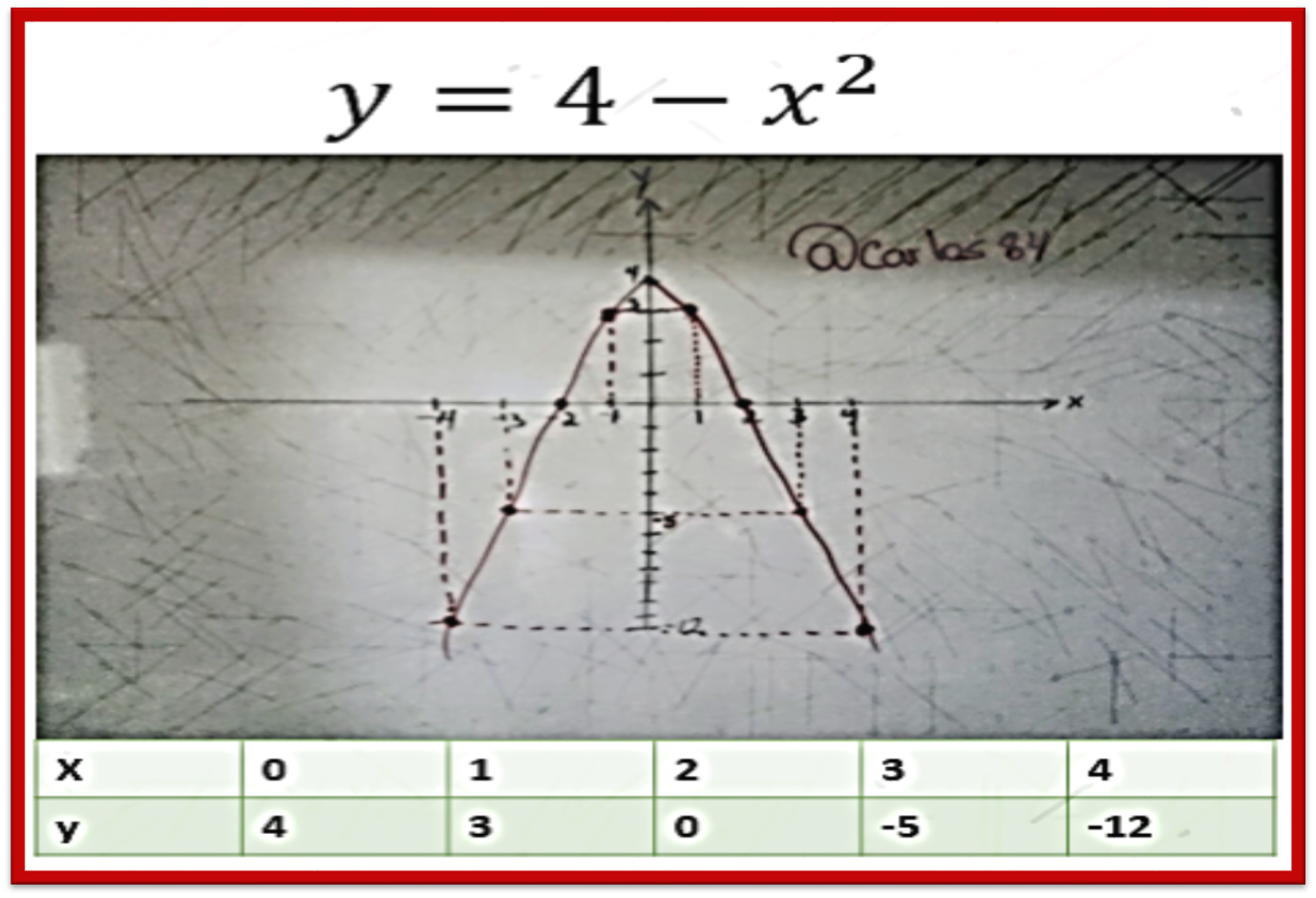
Already having all this information we can plot the function in the Cartesian plane (x,y plane), for this I want to vary a little, so I am not going to plot it with the geogebra software, but I am going to plot it on the blackboard of my house, as follows:

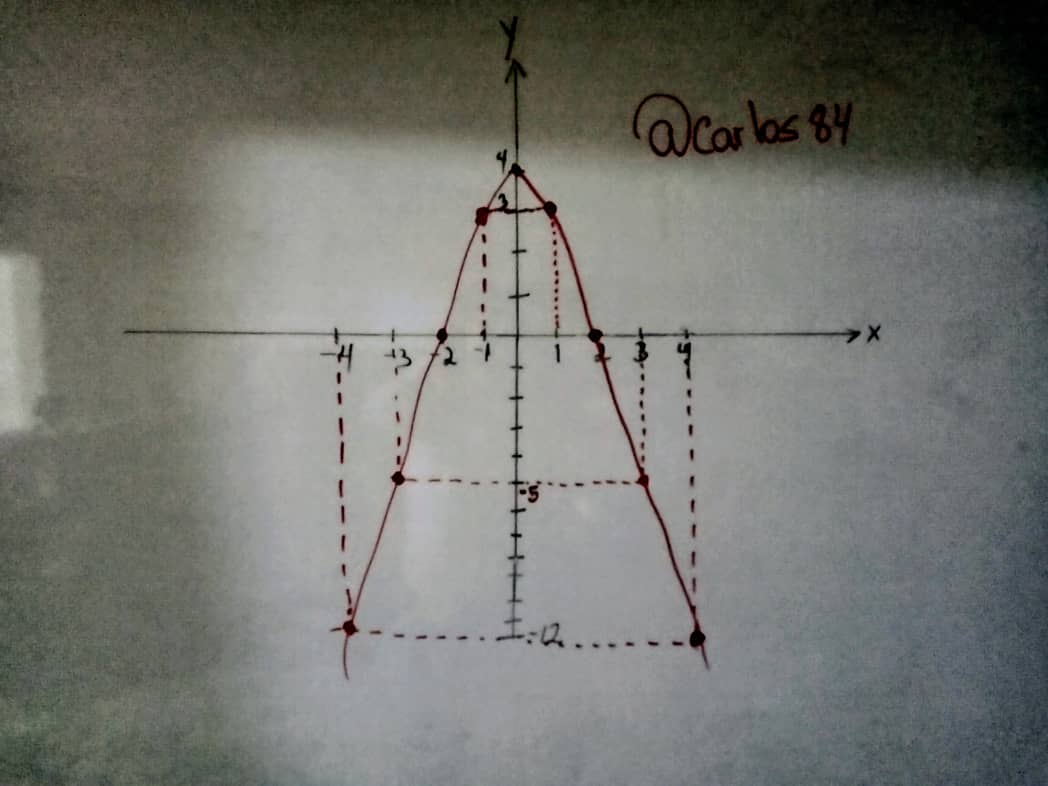
We can see in the previous graph that there is a symmetry of the function with respect to the y-axis.

The domain of the function is all the real numbers.

The Range of the function is (-∞;4]

The function grows in the interval (-∞;0]

The function decreases on the interval [0;∞).

Bibliographic Reference

Calculus with Analytic Geometry by Ron Larson, Robert, P. Hostetler and Bruce H. Edwards. Volume I. Eighth Edition. McGraw Hill. Año 2006