Optimization problem by means of the derivative of a function: Calculation of a minimum length

Image source

Hello friends and followers of STEM content, this time I want to explain a form of optimization by applying the derivative, for it will be proposed to solve an exercise of real life, as shown below:

Two poles are 30 feet apart. One pole is 12 feet high and the other pole is 28 feet high. The poles are to be connected by a cable that is tied somewhere in the ground between them.

At what point should it be tied to the ground in order to use as little cable as possible?

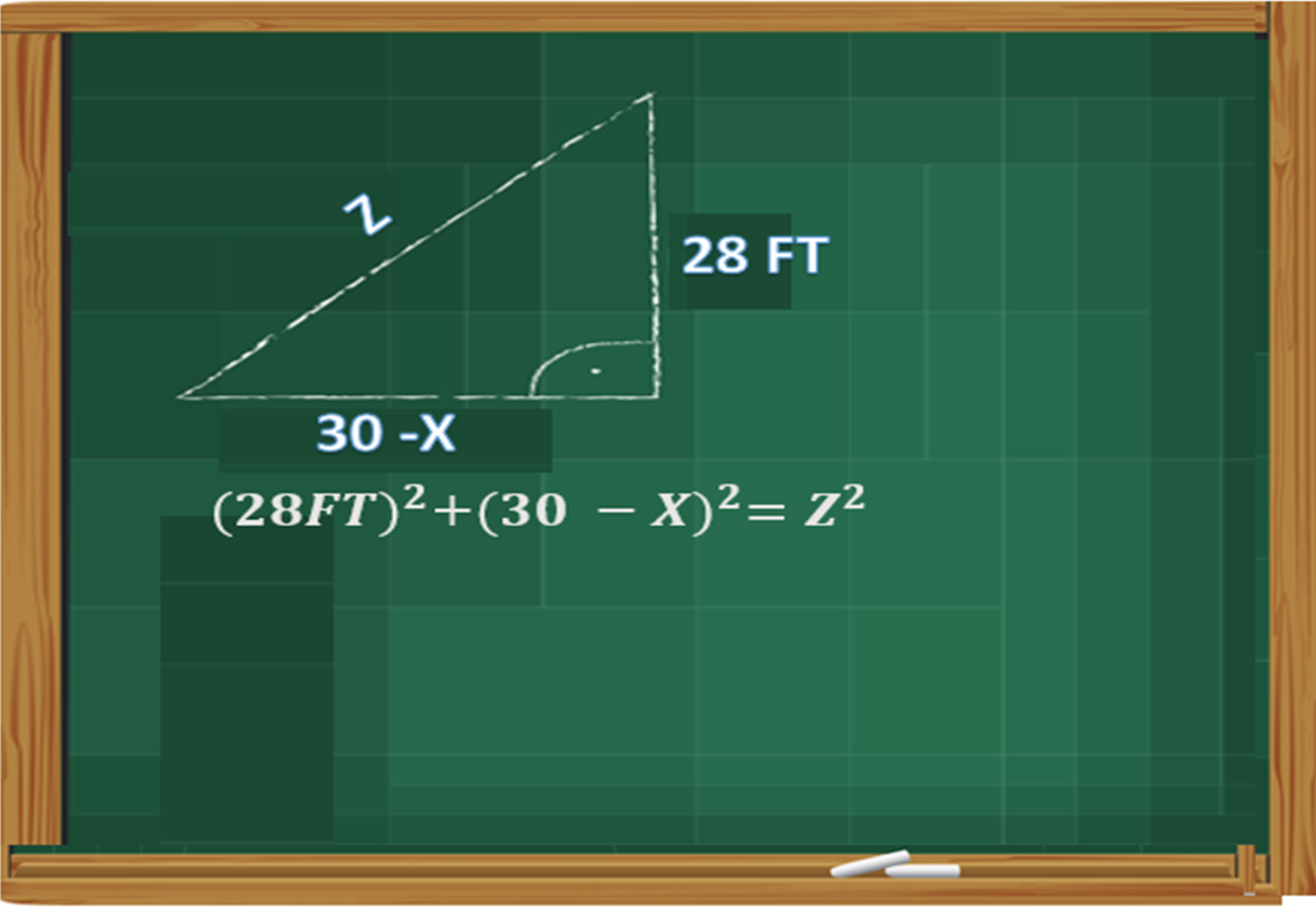
Below is an image prepared by me (@carlos84) alluding to the representation of the exercise:

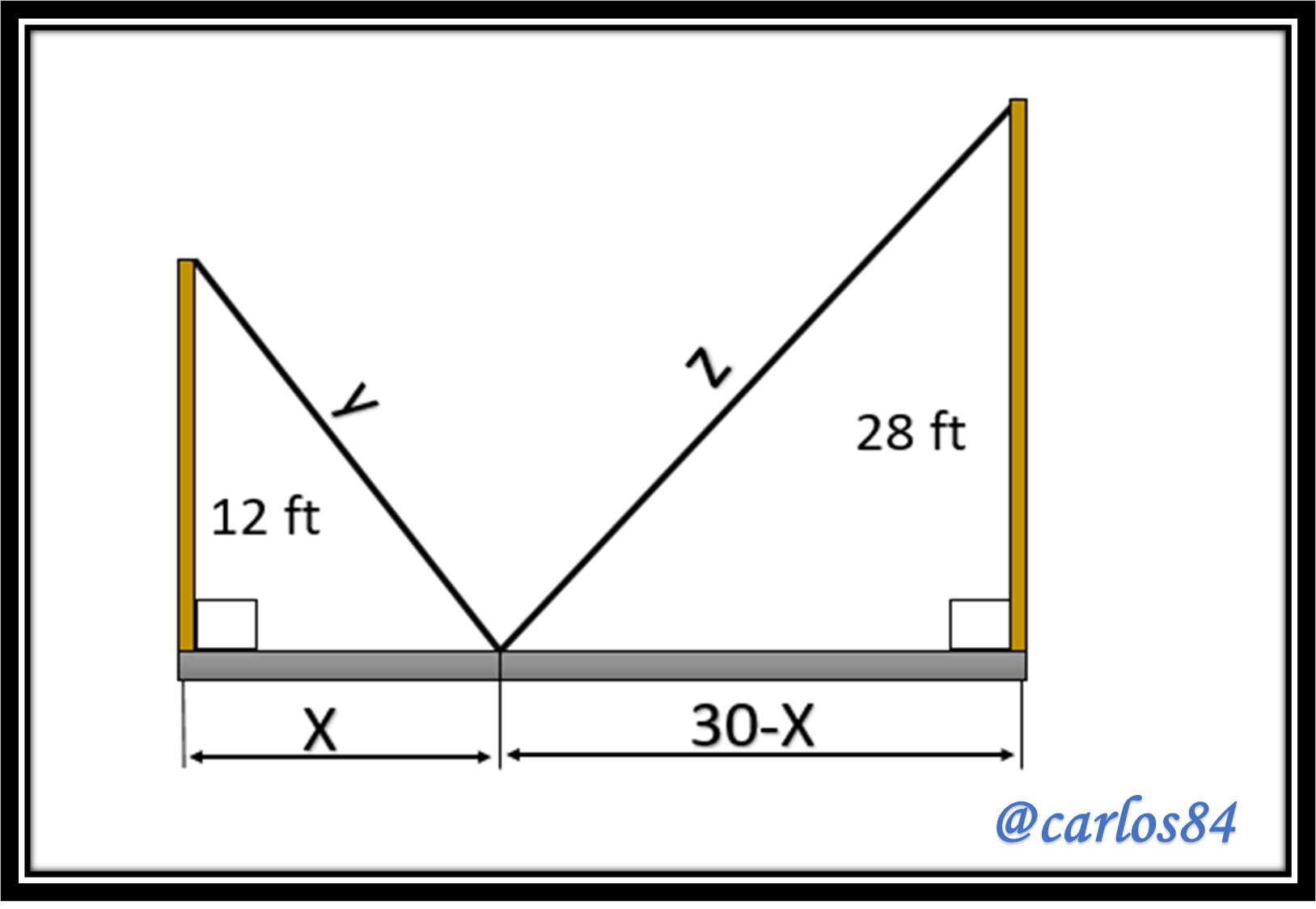
As can be seen in the picture above, Y: is the length of the cable from the top of the 12' pole to any point on the floor. Z: is the length of the cable from the top of the 28-foot pole to the same point on the floor where the cable from the 28-foot pole is connected. The length from pole to pole is 30 feet. X: is the distance from the bottom end of the 12-foot pole to any point on the ground, from that same point to the point at the bottom end of the 28-foot pole is the distance: 30-X.

We have two right triangles:

• Pole length of 12 feet: where: the adjacent leg is X, the opposite leg is 12 feet and the hypotenuse is Y.

Image edited from pixabay

• Pole length of 28 feet: where: the adjacent leg is 30 - X, the opposite leg is 28 ft and the hypotenuse is Z.

Image edited from pixabay

In this post we are using a very important term which is to optimize, since placing the cables to tie the poles at a specific point can waste the least amount of cable possible while maintaining the safety standards required by the operation.

Image source

One of the first aspects we should consider as the cable length to be optimized to Y + Z = W, so the cable length optimization function is going to be W, which in turn is going to be the sum of Y and Z.

Solution to the problem

As we must add: Y + Z to find the optimization function W, we must apply the Pythagorean theorem to get the value of Y and Z, as follows:

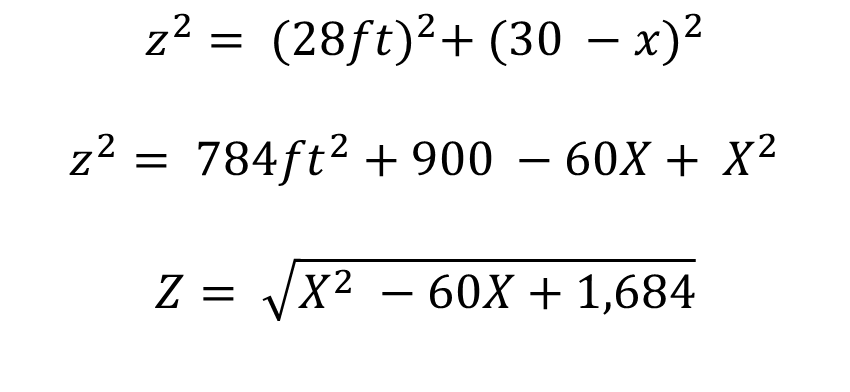
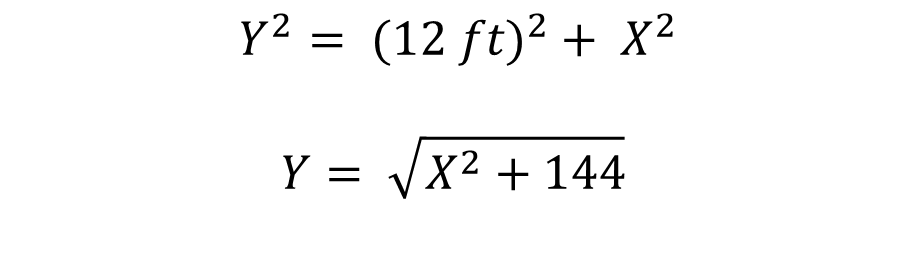
Since to optimize for this case is to spend the minimum amount of wire of the function W, it implies that the function W reaches optimality by equaling the first derivative to zero, i.e. W' = 0 and since W = Y + Z, it implies that

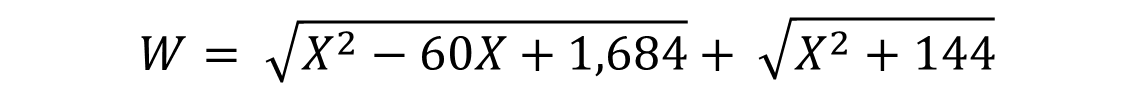
To find the derivative of the optimization function W we proceed as follows:

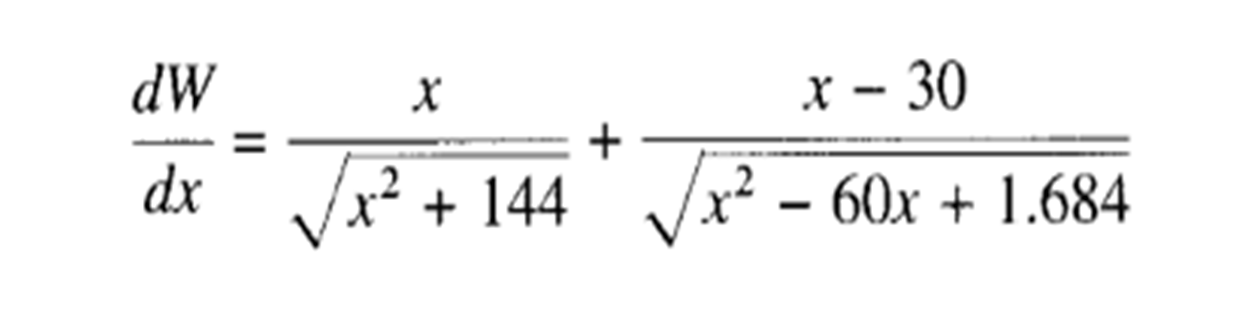
We proceed to equal the derivative to zero:

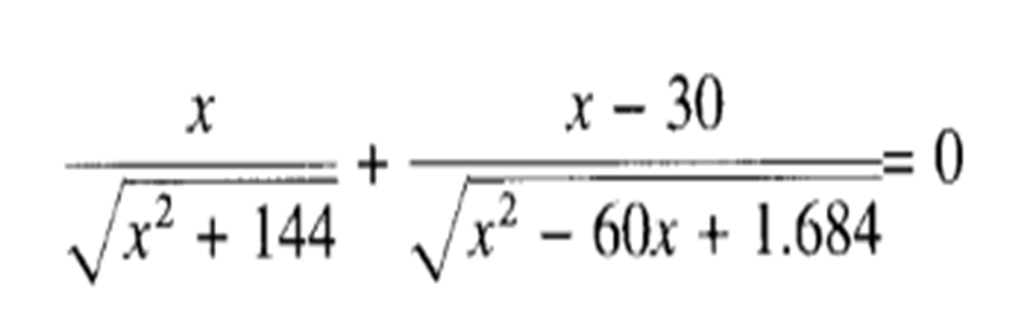
We solve the equation and find the values of X:

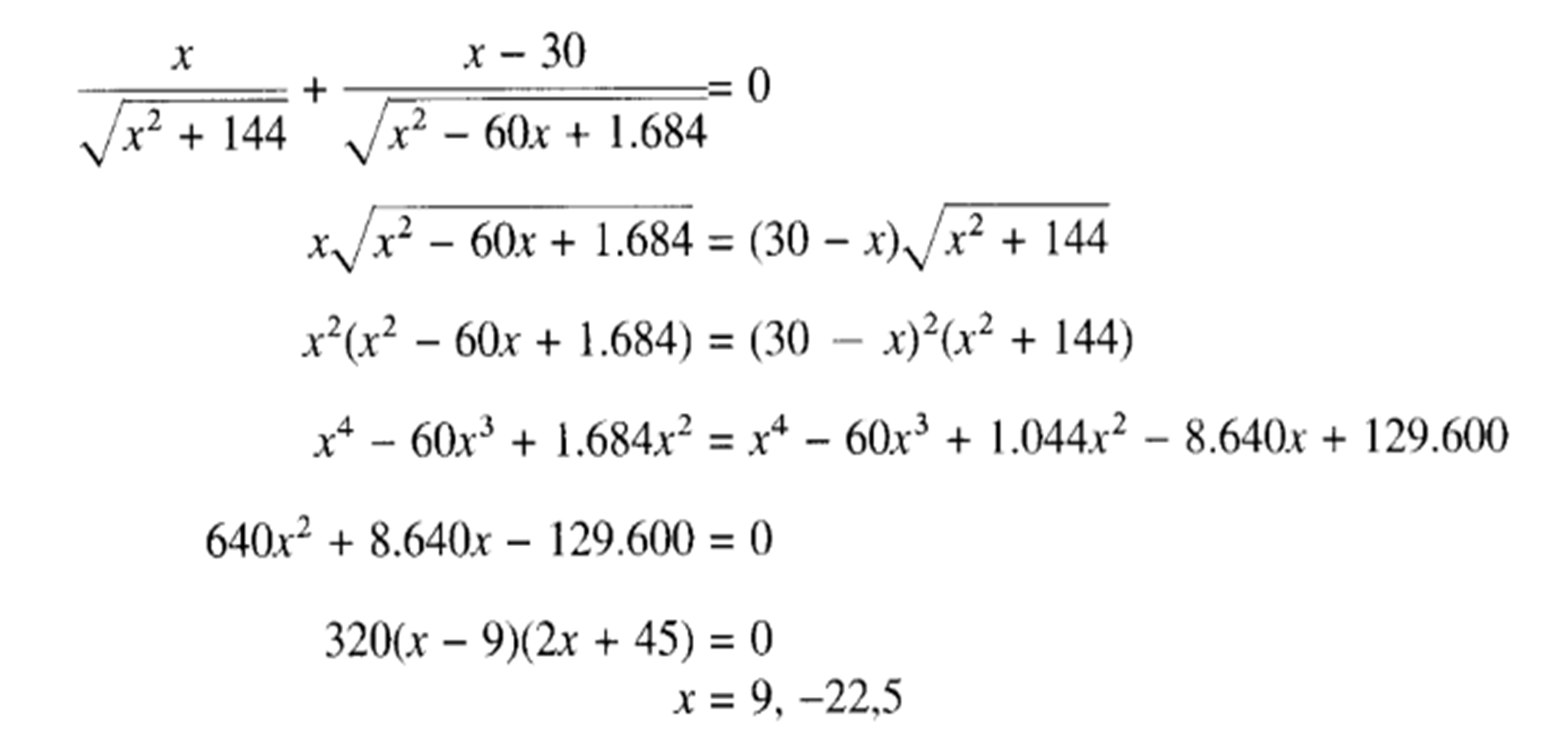
He gave us that

X = 9
X= -22.5

However the distance of -22.5 is not within the range of [0 , 30], so of the two options we choose X = 9.

Which means that in order to spend less amount of cable we should tie the cable at 9 feet from the pole which is at a height of 12 feet and in that way we are ensuring that the operation guarantees safety while at the same time spending the right amount of cable which is the important thing about the optimization process.

Referencia bibliográfica recomendada

• Calculus book with Analytic Geometry. Volume I. Author: Larson and Hostetler. 7th edition.