Multiple integration exam of the subject Calculus III (considerations on how to solve it)

Hello friends and enthusiasts of the academic and educational content that we share here in the educational community with the interest of disseminating the educational strategies that we educators of the world use to educate young people at all levels of education.
In this opportunity I would like to share with you some considerations on how to solve a written exam that I gave to my university calculus III students.
In Calculus III, students must have previous knowledge of Calculus I and Calculus II. This is because most of the content taught in Calculus III are, for example, functions, limits, derivatives and integrals: functions, limit, derivatives and integrals, with the difference that in calculus III the functions are with two variables, the limits are solved for functions of two variables, the derivatives are solved partially, since the derivatives that are solved are of functions of two variables, the process to solve an integral is also different, since they are integrating functions of several variables, so it is very common to find multiple, double and iterated integrals such as those presented as an example in the resolution of the exam model proposed in this post.
Let's start with the first exercise.

It is an iterated double integral, whose limits of integration go from zero to two in the first integral and from zero to one in the second integral.
The integrand is composed of three terms, therefore each of the terms must be integrated with respect to the variable Y and then be evaluated at the limits of integration [0;1]. It is important to note that these limits of integration are substituted in the Y variable. Then the remaining integral with respect to the variable X is solved and evaluated at the limits of integration [0;2], the procedure follows:
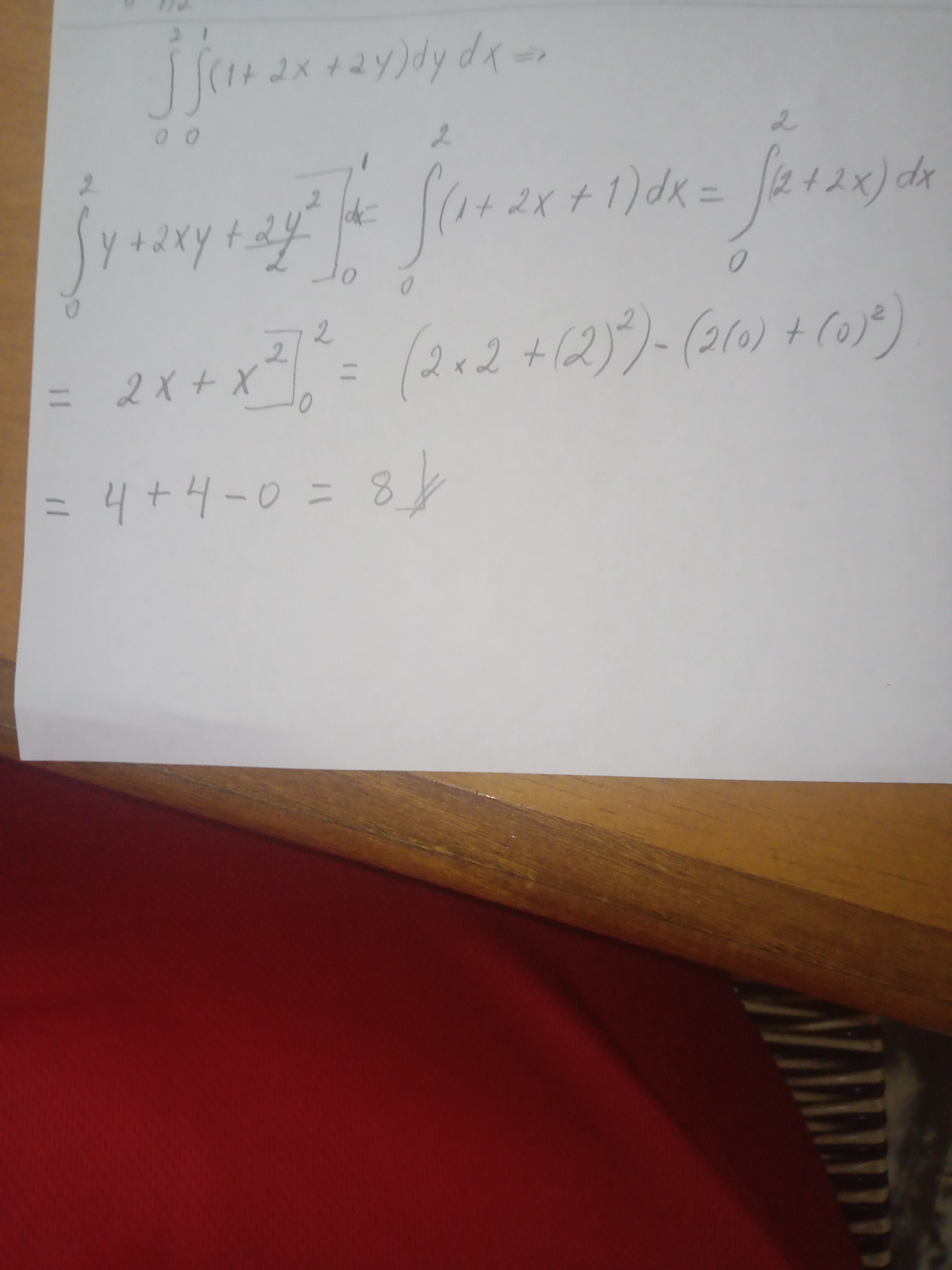
Exercise number two is an integral that is solved in the same way as the integral of the first exercise, however the only difference is that it has different limits of integration, let's see how it is solved:

For the third exercise it must be taken into account that it is not a double integral, it is an iterated simple integral but of an integrand is a function of two variables (X;Y).
The function of the integrand has the particularity that the Y variable is a constant since the integral must be solved with respect to the X variable.
When we solve the integral with respect to X, we must apply the method of substitution or change of variables, where U= Lnx and its derivative is dx/x, it is solved as follows:
One of the convenient steps to follow to solve this integral is to solve the indefinite integral which is solved by the method of substitution or change of variable:

The last exercise is solved as follows:

Note: all images shown in this post were photographs taken with my smart phone blu
Recommended bibliographic reference
Calculus with Analytic Geometry. Author: Larson and Hostetler. Volume 2.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.