Geogebra software technology applied to the calculation of the area of intersection between two real functions

Hello friends and lovers of STEM content, this time I want to vary a little my blog, that is why I want to present for this case a topic of the subject of calculus that I teach at the Southern Experimental University of Lake Jesus Maria Semprum (UNESUR).

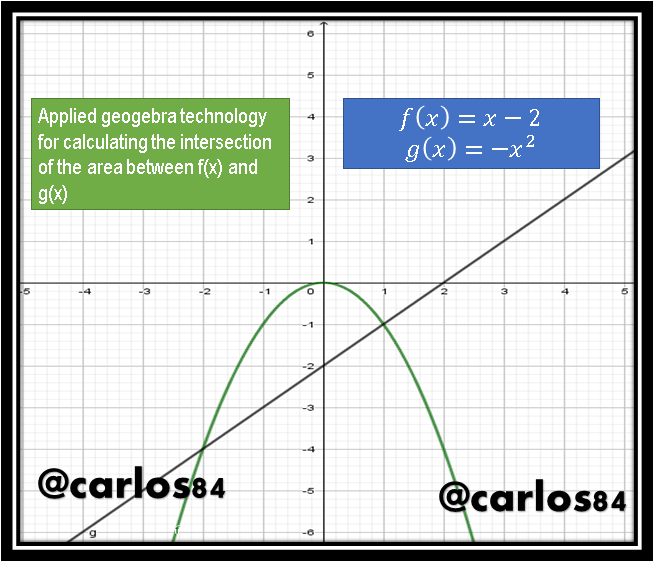
The topic to be discussed is to find the area of intersection between two real functions, this time the real functions are the line f(x)= x-2 and the parabola g(x)= -x².

For this case we are going to use the geogebra software technology to know the coordinates of the intersection points of the two functions in the Cartesian plane and to know exactly the region of intersection to which we are going to find the area.

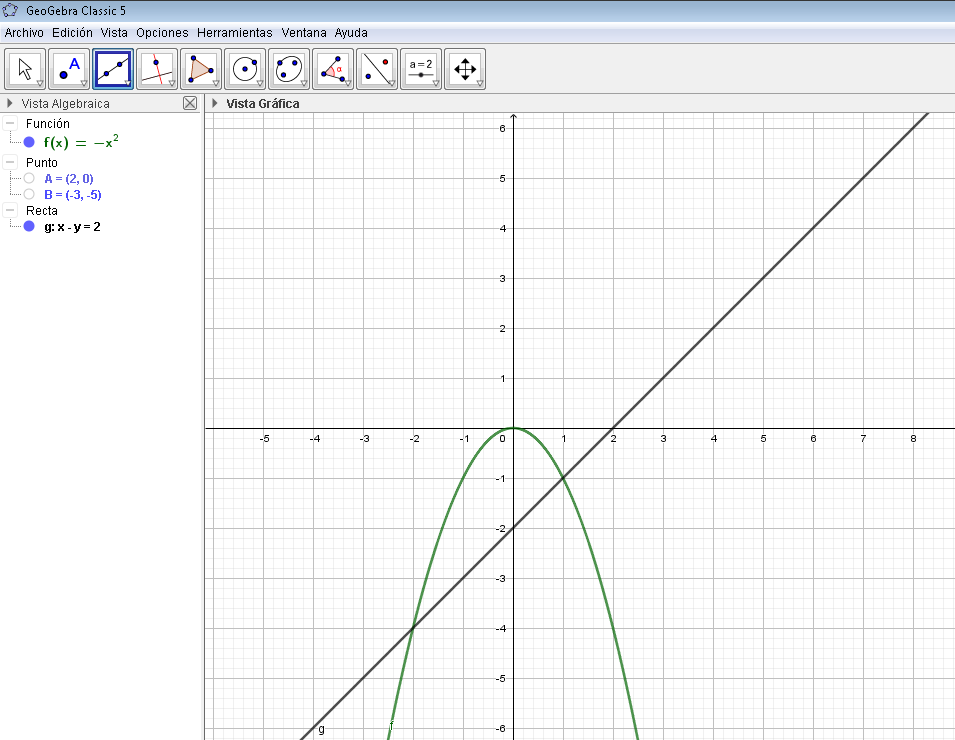
As it can be observed in the previous image the function that is above is the parabolic function and the one below is the linear function, and the coordinates in the X axis of the intersection points are displayed in an interval that goes from -2 to 1.

Taking into account this information, thanks to the fact that we were able to rely on the geogebra software technology, we do not have to find algebraically the coordinates of the intersection points, we do not have to find the points of cuts with the coordinate axes, but we simply consider the formula for calculating the area between the intersection of two real functions.

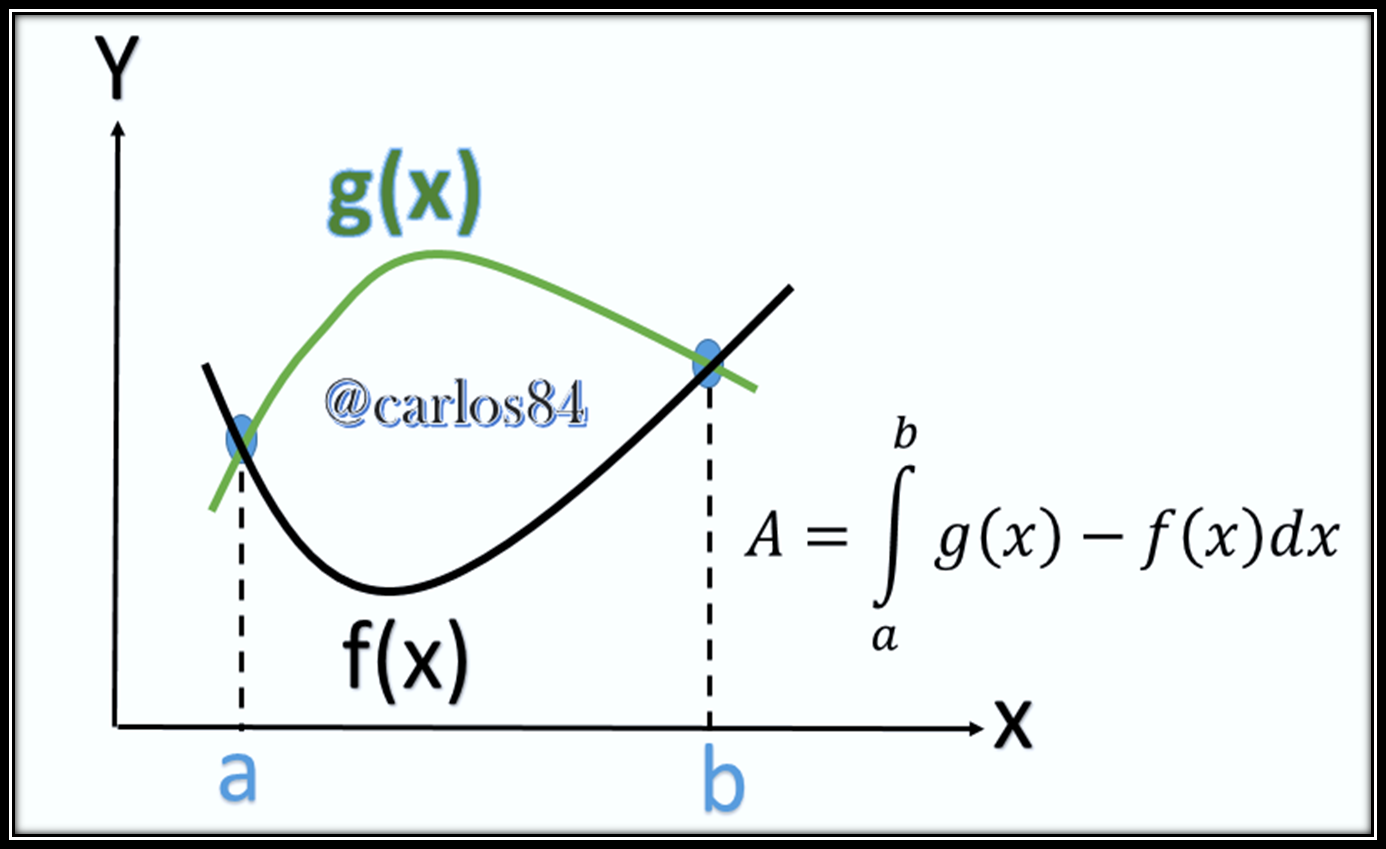
Therefore, what we would have to do is to calculate the area applying the formula shown previously, where the limits of integration would be a= -2 and b= 1, the function above is g(x) = - x².

The one below is f(x)= x-2, so the approach for calculating the area between the intersection of the two functions is:

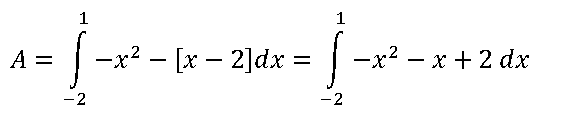
To solve the definite integral, the first thing to do is to solve the indefinite integral and apply the fundamental theorem of calculus:

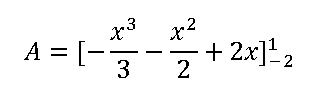
To apply the fundamental theorem of calculus we simply substitute in the variable x the upper limit and subtract the substitution of the lower limit:

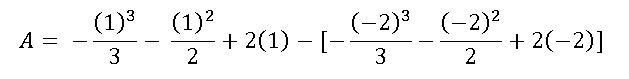
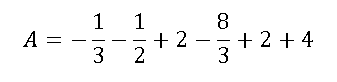
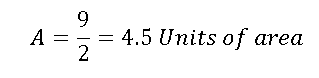
Conclusions

• With the application of geogebra software technology we can find the region of the plane where the two real functions intersect, and with this we simply save the step to be able to graph, and in this way we can directly apply the calculation of area between the intersection of the two functions.

• Obtaining the exact region of intersection minimizes the errors at the moment of knowing which are the limits of integration in the area calculation.

• The application of the integral for the calculation of the area between the intersection of two functions is very necessary since this type of regions in the plane are regions that do not delimit exact geometric regions such as rectangles, triangles, circles, among others, and that on the contrary are regions of the plane where the calculation of its area is only possible with the application of the integral for the calculation of area.

References

Larson's calculus book. 7th edition. Volume I.

Note: all images are my own and were created using Microsoft PowerPoint design tools.