Find the area under f(x) by solving a neperian logarithm integral.

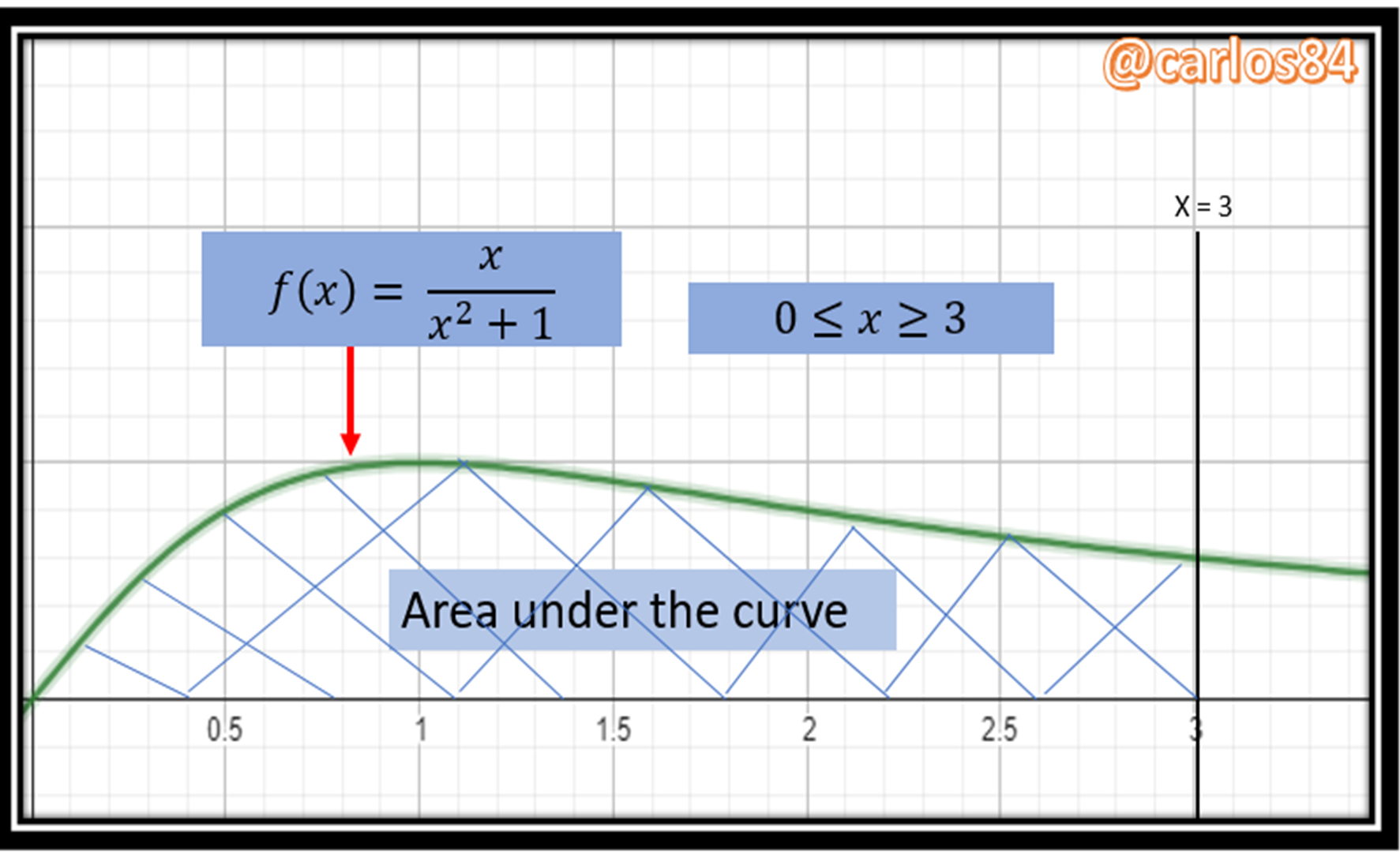
Hello friends and followers of STEM content, this time I want to explain how to calculate the area under the curve of a rational function by means of an integral that is solved by the neperian logarithm rule.

The function to which we are going to calculate the area is the region bounded by:

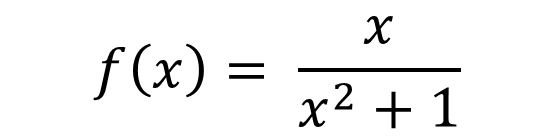
the x-axis and the vertical line x= 3

The graphical representation of the requested area is:

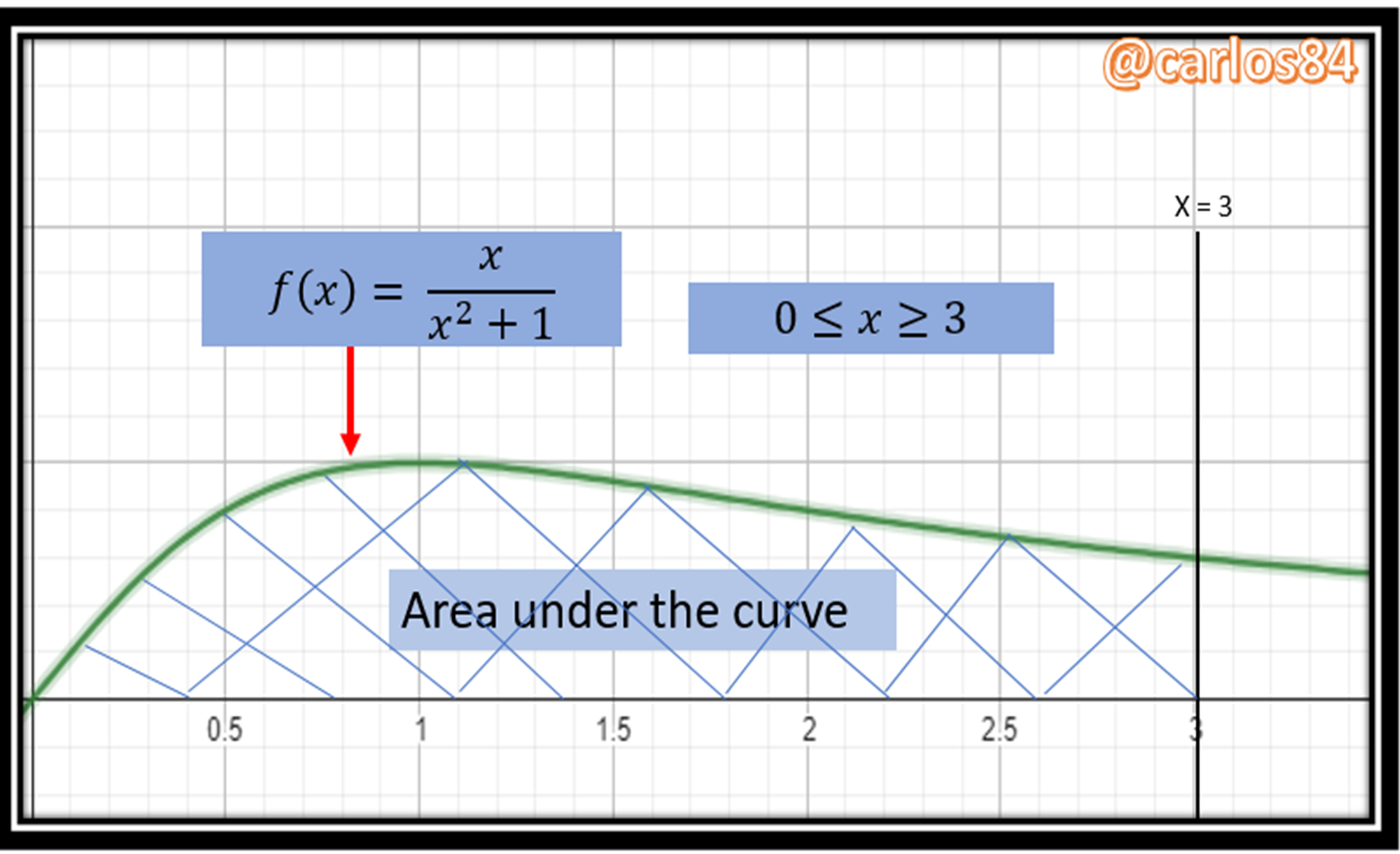
The solution to find the area between the curve, the x-axis and the vertical line x = 3 is by solving the following definite integral:

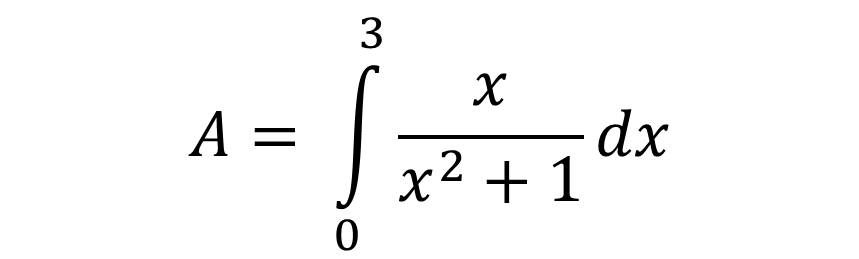
To solve the definite integral we first solve the indefinite integral:

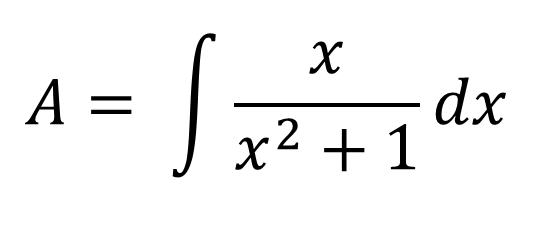
The result that gives us the resolution of the indefinite integral we evaluate it in the interval x [0 , 3] applying the fundamental theorem of calculus:

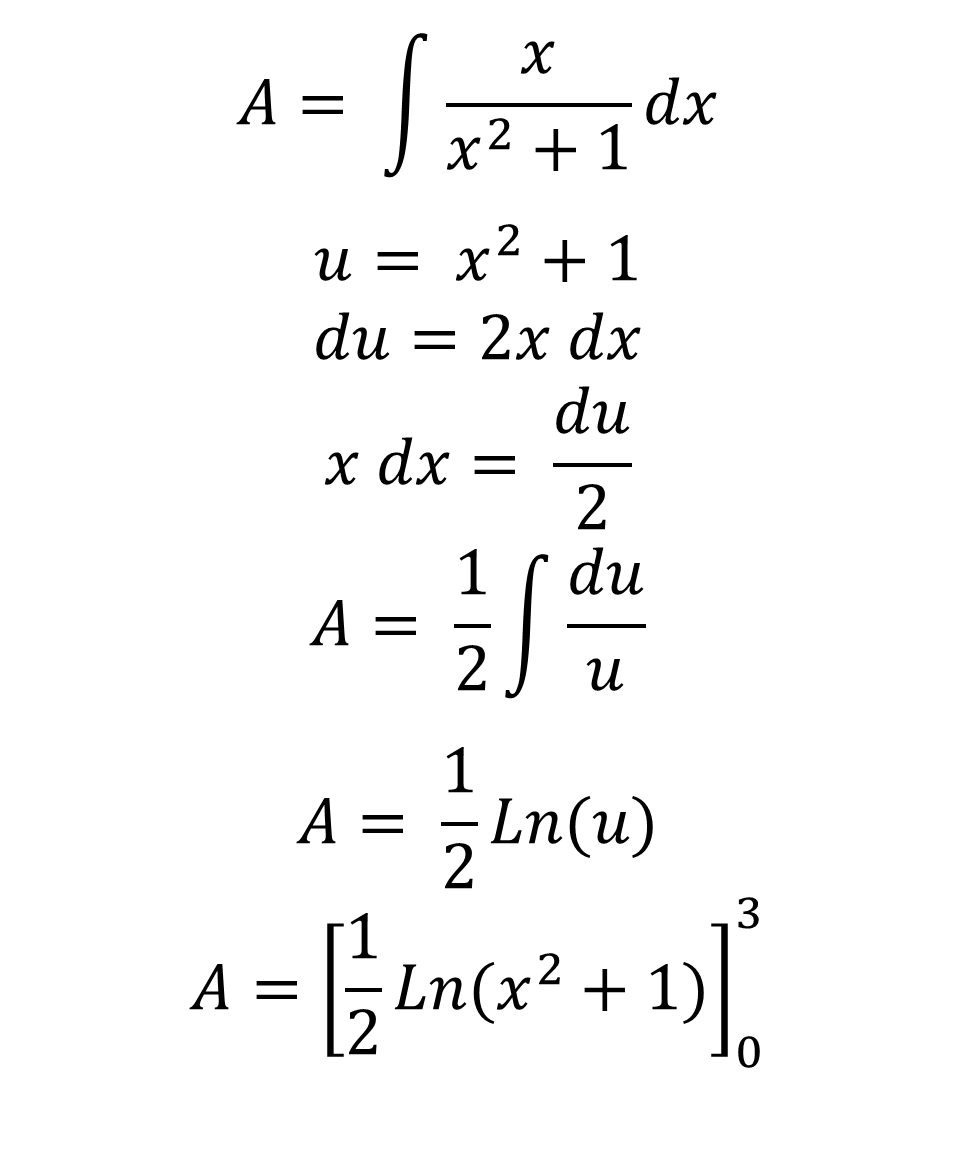
Then we apply the fundamental theorem of calculus:

Conclusion

Applying the basic rule of integration of Neperian Logarithms we can calculate the area under the curve of a rational function, what we have to have defined is the area of the limited region and to be able to consider the integral, for this case the area gave us equal 1.151 units of area.

Recommended Bibliographic Reference

Calculus book with Analytic Geometry by Larson and Hostetler. Volume I. 7th edition.

Note: All equations were prepared using the equation insertion tools of Microsoft PowerPoint. The graphs were generated with geogebra software.