Can a quadratic mathematical model be constructed from a table of consumer price index data as a function of time?

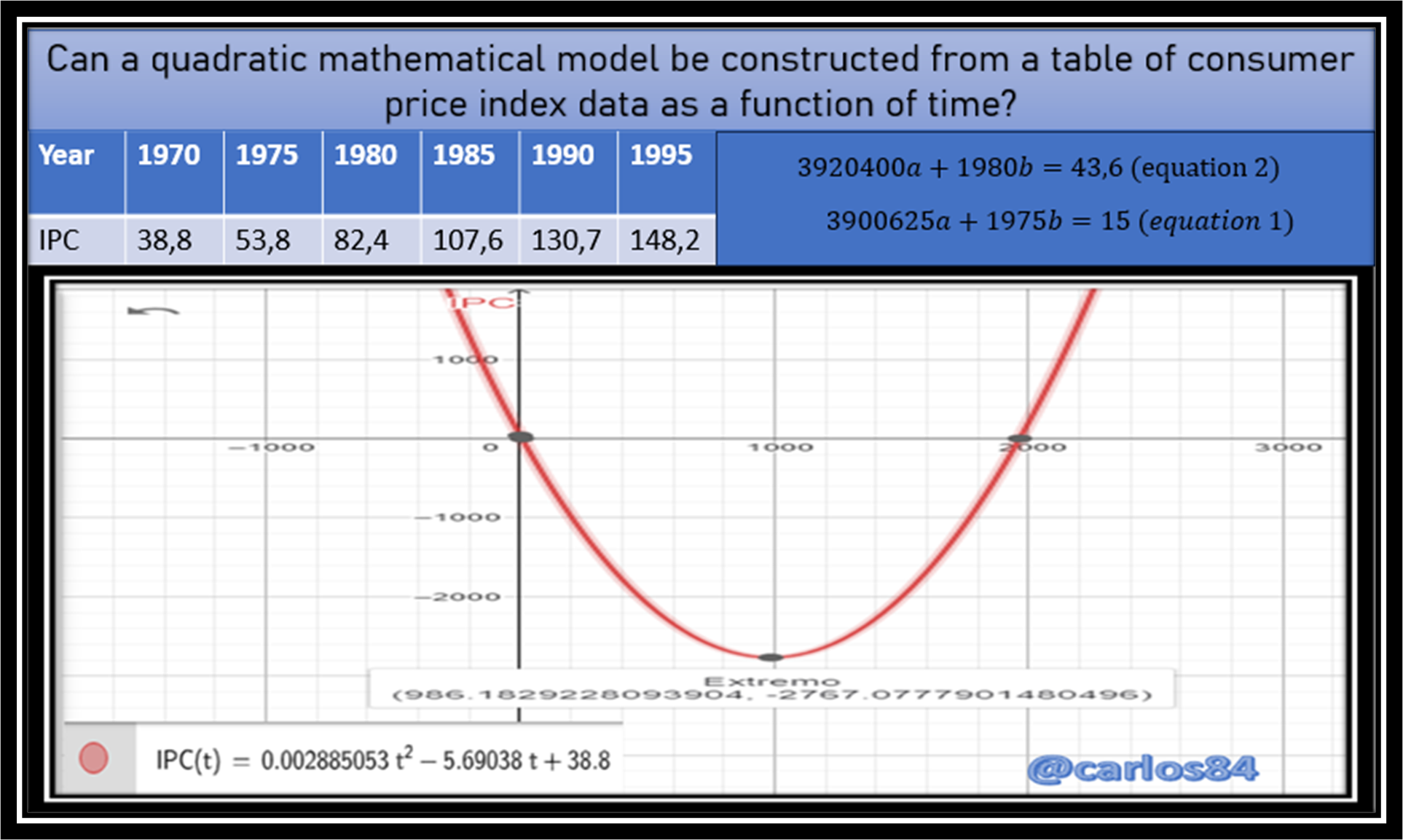
Hello friends and followers of STEM content, this time I want to explain how to generate a quadratic mathematical model from a data table, in this case the data table is:

CPI stands for Consumer Price Index.

The following is requested:

[1] Find a mathematical model of the form y=at^2+bt+c that fits the data. y=IPC and t is the time measured in years, it is important to consider the origin as t=0 in the year 1970.

[2] Apply the model to predict the CPI for the year 2000.

Solution to the problem

To find the mathematical model whose representation is a quadratic function of the form:

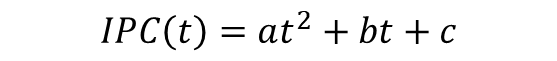
We start by saying that when t=0 we are in the year 1970, where CPI = 38.8, which implies that:

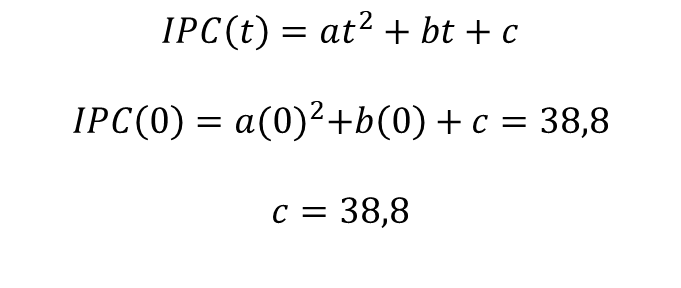
Under the above deduction we have that c=38.8.

When t=1975, it implies that CPI = 53.8, therefore:

To get equation 2, we must consider minimum another point, so I will consider t= 1980 and CPI= 82.4, therefore:

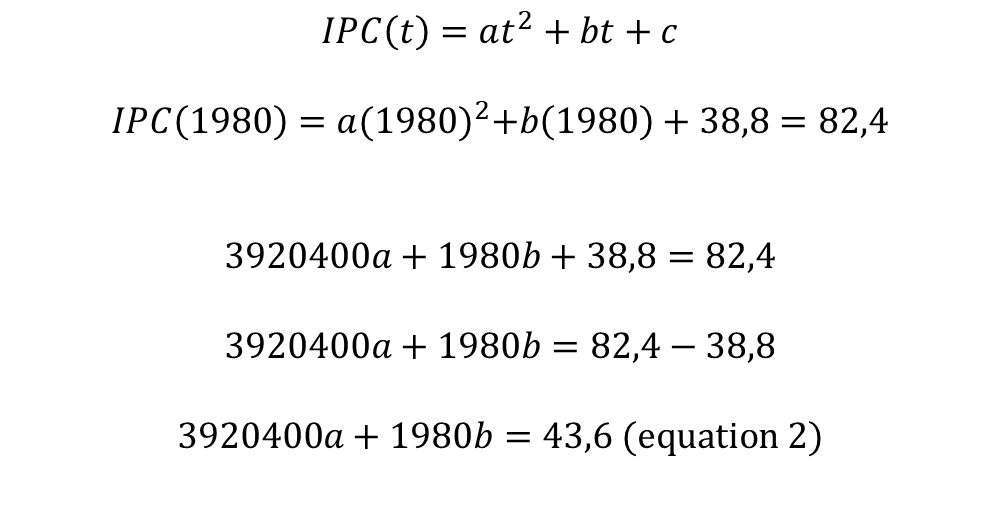
Given equation 1 and equation 2, we solve this linear equation system by the elimination method:

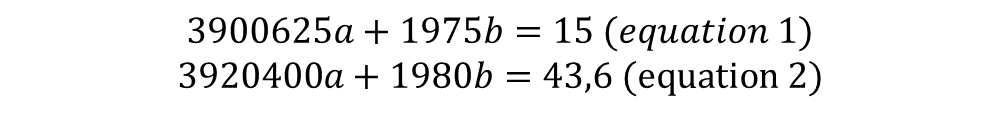
To eliminate b, we multiply all of equation 2 by -1975, and multiply equation 1 by 1980:

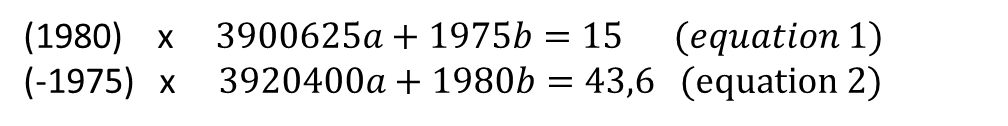
We find the value of a:

Already having the value of a=0.002885053 we substitute in:

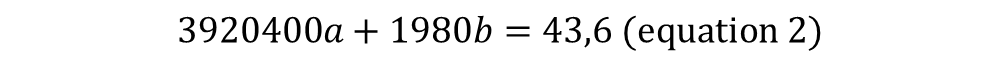
As follows:

Already having the values of a = 0.002885053 , b = -5.69038 and c=38.8 we can find the mathematical model of the form y=at^2+bt+c that fits the data, therefore the quadratic mathematical model is:

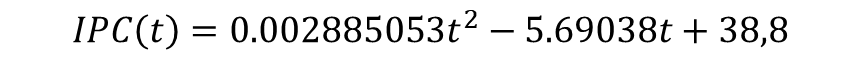
To apply the model to predict the CPI for the year 2000, we simply substitute t = 2000 in

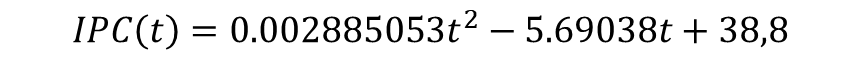
The quadratic mathematical model can predict that in the year 2000 the consumer price index (CPI) is $198.252, which if we compare it with that of 1995, which is $148.2, we realize that it has increased by $50.

We could also ask ourselves:

In which year is the lowest consumer price index (CPI) perceived?

To do this we will plot in GeoGebra the quadratic model

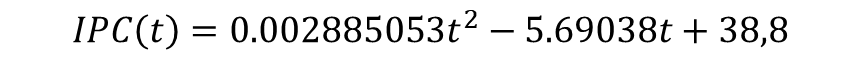
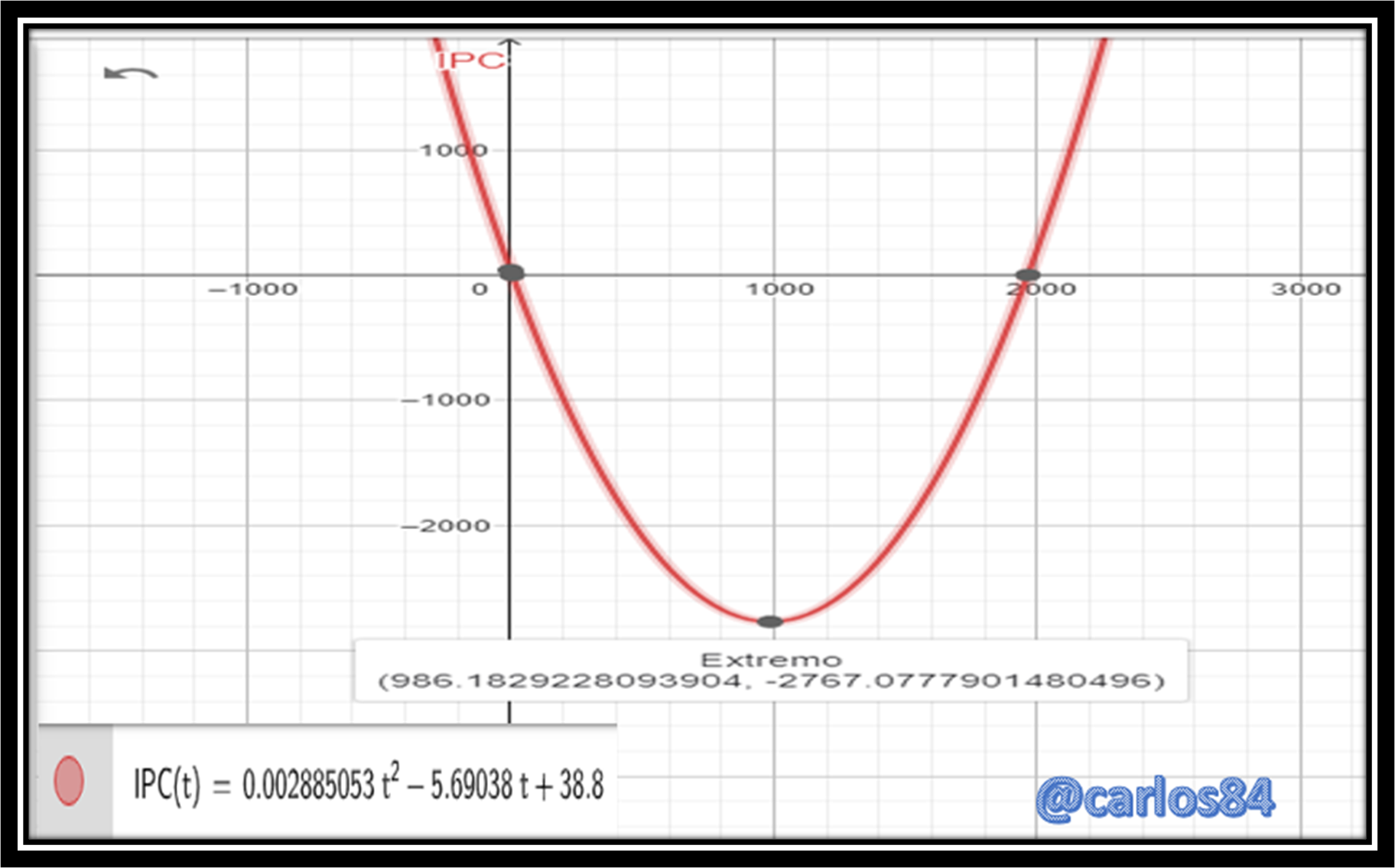
Since the graph of the quadratic model is a parabola that opens upwards, it implies that the year with the lowest consumer price index (CPI) is at the vertex of the parabola.

The vertex of the parabola is at the point (986.18 ; -2767.07), which means that the lowest CPI is -2767 dollars and it was in the year 986, after the year 986 is that we see that the CPI claims to increase significantly.

Recommended reference

Calculus with Analytic Geometry. Author: Larson and Hostetler. Volume I. 7th edition.

Note: All the equations were elaborated using the Microsoft PowerPoint insertion tools. The parabolic function graph was generated using GeoGebra software as a tool.