Applications of the derivative to economics and commerce

Although the most common way to analyze rate changes is when a variable changes with respect to time, however in this case we have an application of the derivative in economics and commerce, in which there are rates of change that are not measured with respect to time, these rates of change studied in economics are called marginal benefit, in which the changes that are obtained due to the costs obtained in producing a certain amount of a product that is for sale are studied, knowing that income benefits are obtained from the sales of such products.

The purpose of this post is to explain how the derivative can mean a very effective application that helps us to understand this rate of change in the economy in relation to the costs obtained by producing a certain amount of a product, for this we will present an example in which I will calculate the marginal benefit given the cost of production to produce a certain amount of a product.

Equations involved

Example in calculating marginal profit given the cost of production of the number of units produced (sold)

The production cost of x quantity of shoes produced is given by the following cost function:

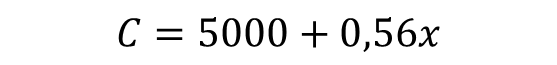
The monthly demand for shoes is given by the following expression:

Find the total profit and marginal profit for: x= 20,000 units of shoes produced.
Para hallar el beneficio total (P)

P = R - C

R = xp, which implies that:

Therefore P = R - C is:

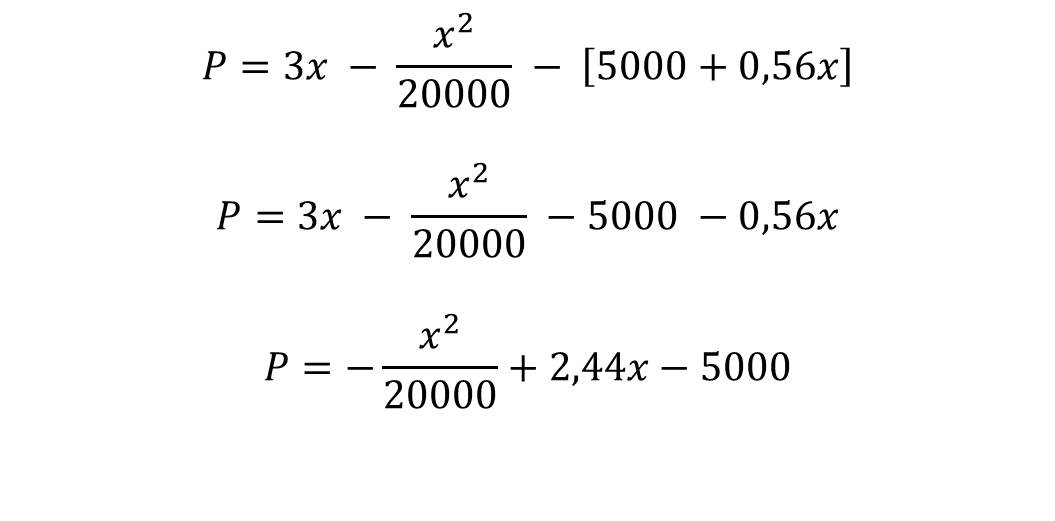
To calculate the marginal benefit, the function P is derived as follows:

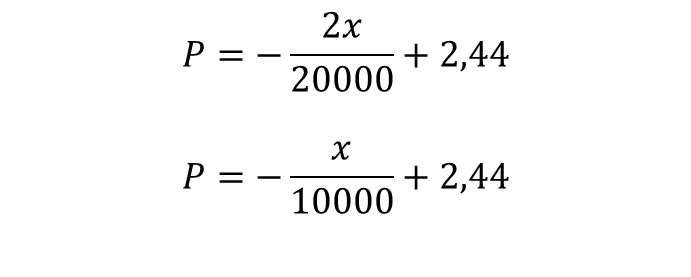
To calculate the total profit, the production value is substituted:

x = 20000 units of shoes

In the original P function:

For x = 20,000 units of shoes the total profit is:

This means that when 20,000 shoes are sold, there is a cost of $16,200 and a total profit of $23,800.

To calculate the marginal profit for when x= 20,000 shoes are sold, we substitute x = 20,000 in the derived P function:

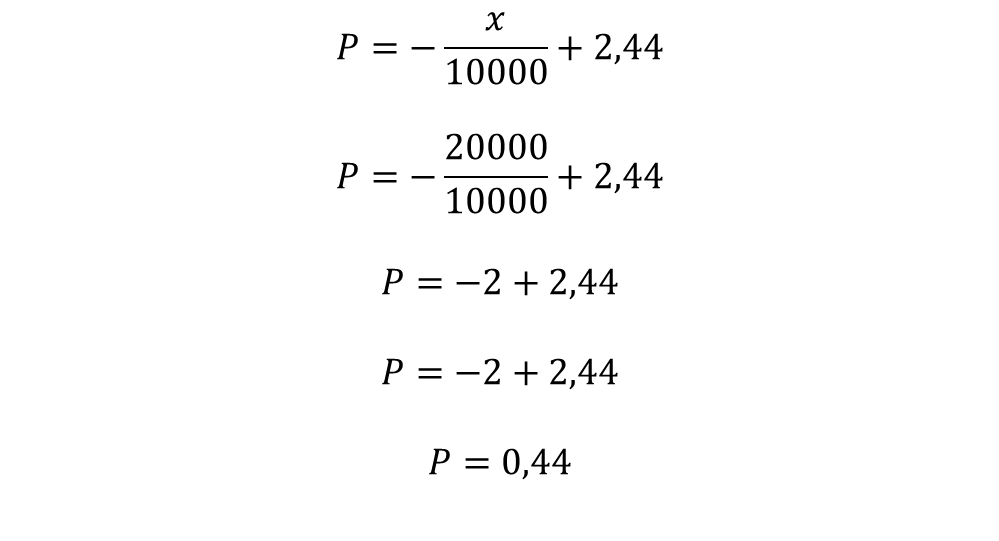
This means that when 20,000 units of shoes are produced, a marginal profit of $0.44 is obtained.

Conclusion

Marginal profit as a function of shoe units produced varies according to:

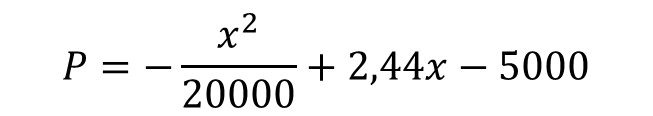
This function is a parabola that opens downward, so there is a maximum point where it reaches the highest value, so the marginal profit is achieved when the slope of the tangent line to the parabola is horizontal, and that is when the total profit function is derived and is equal to zero. Which translates into:

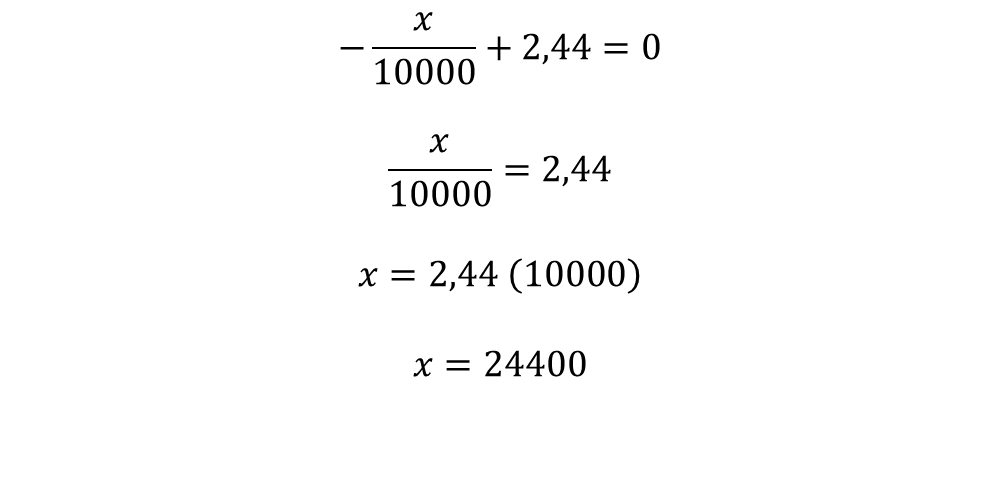
This means that when the quantity of 24400 shoes is produced is when the greatest amount of profit is obtained, since when a greater quantity of 24400 shoes is produced, the marginal profit will decrease. An example of this can be seen when 30000 shoes are produced to find out what the marginal profit is:

What we can observe is that when a quantity of shoes greater than 24400 units is produced, the marginal profit starts to be negative.

Recommended bibliography

Calculus with Analytic Geometry. Volume I. 7th edition. Author: Larson and Hostetler.

Note: All equations in this post were prepared using Microsoft PowerPoint equation insertion tools.