Introducción

En esta oportunidad quiero tratar un tema dentro del cálculo diferencial que tiene una gran relevancia en lo que concierne a una aplicación directa que tiene la derivada usando simplemente su definición.

Cuando se tiene una función polinómica y le aplicamos el proceso de derivación, y al resultado obtenido le sustituimos el valor de la coordenada x del punto en donde es tangente a la curva, estaríamos completando entonces en esencia el verdadero significado de esta operación, quizás hoy en día en muchas universidades se vea sencillo, pero en los tiempos antiguos existieron matemáticos como Isaac Newton y Gottfried Leibniz que lucharon mucho tiempo para poder descubrir lo que quizás yo en cortas líneas logre demostrar en lo referente al cálculo de la pendiente de una recta que es tangente a cualquier curva en un punto.

El objetivo de esta publicación es tomar el ejercicio propuesto #7 del libro de cálculo con geometría analítica de Robert Larson volumen I de la página 104 del capítulo II para resolverlo en función de la aplicación que tiene intrínsecamente la derivada para conseguir el valor de la pendiente de la recta tangente a cualquier punto de la curva.

Los datos que se van a elegir son una función cuadrática y las coordenadas de un punto en donde pasa una recta tangente en ese mismo punto a esa función parabólica.

Para realizar la demostración de que realmente la derivada funciona como una herramienta ideal para conseguir la pendiente de una recta tangente a cualquier punto de una función polinómica, se tomaran dos puntos cualesquiera de la recta y se calculara la pendiente utilizando los conocimientos clásicos que nos brinda la geometría analítica.

Lo otro a considerar en la propuesta demostrativa que se realizara en este post es presentar ante ustedes el gráfico de la función cuadrática (parábola) con la recta que es tangente al punto seleccionado. El gráfico se realizara empleando el software de uso libre geogebra 5.0.

Ejercicio propuesto # 7 del libro de cálculo de Larson volumen I. Capitulo II página 104

Encontrar la pendiente de la recta tangente a la gráfica de la función en el punto dado:

Función polinómica: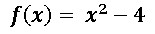

Coordenadas del punto tangencial: (1; -3)

Como se puede analizar en este caso, el libro de Larson en este ejercicio propuesto básicamente lo que nos pide encontrar es el valor de la pendiente de la recta que pasa por el punto tangencial a la parábola (función cuadrática).

¿Cómo debemos asumir la solución al problema planteado?

Para ello voy a citar textualmente la siguiente conceptualización entendida por mi de lo que es la definición geométrica de la derivada, que dice así:

"Cuando se realiza el procedimiento matemático para encontrar la derivada de una función real, realmente lo que se esta es encontrado es el valor de la pendiente de la recta que es tangente a la curva en un punto."

Teniendo en cuenta esta conceptualización podemos deducir entonces que para encontrar el valor de la pendiente de la recta que es tangente a la función cuadrática en el punto (1 ; -3) lo que se debe hacer primeramente es derivar la función cuadrática y luego en esa función derivada sustituir la coordenada x del punto (1 ; -3), el valor que nos arroje la sustitución de la coordenada x del punto (1 ; -3) será el valor de la pendiente de la recta que pasa por la función parabólica en el punto tangencial (1 ; -3).

Solución para encontrar la derivada de la función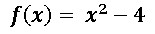

Para derivar esta función cuadrática mi propuesta es realizar su derivada por medio de las reglas básicas de derivación.

La primera regla básica de derivación que vamos aplicar es la siguiente:

• Cuando la función que se va a derivar tiene términos sucesivos se aplica la siguiente regla de derivación:

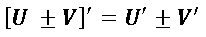
Esta expresión nos dice que si vamos a derivar una función que posee dos o más términos, simplemente derivamos cada uno de sus términos, por lo que nos quedaría lo siguiente:

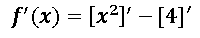
• Para derivar el termino 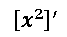aplicamos la siguiente regla de derivación:

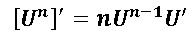
Para aplicar esta regla de derivación básicamente lo que se debe hacer es bajar el exponente, luego restarle la unidad al exponente y finalmente derivar la base. Por lo que la derivada de 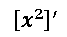es la siguiente:

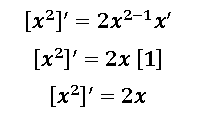
En la derivada de esta expresión hay que hacer una pequeña acotación, y es que la derivada de la base en esta ocación es la derivada de x, y si se busca en las reglas básicas de derivación la derivada de una variable es igual a 1.

• Para derivar el termino 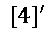debemos emplear la regla básica de derivación de la derivada de una constante, que dice que la derivada de cualquier número real es igual a cero.

• Finalmente nos queda que la derivada de la función cuadrática es

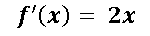
Como se mencionó en la parte de la solución del ejercicio propuesto en este artículo, lo primero que se debe hacer es encontrar la derivada de la función parabólica, lo cual ya se consiguió mediante la aplicación de las reglas básicas de derivación, ahora el próximo paso es sustituir la coordenada en x en la derivada de la función cuadrática.

Por lo tanto la pendiente de la recta que es tangente a la parábola en el punto (1; -3) se calcula como sigue:

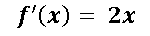
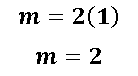
Para demostrar que la el valor de la pendiente de la recta que es tangente a la parábola en el punto (1 ; -3) es el correcto, y que pueda quedar demostrado que la derivada tiene una importancia relevante para calcular la pendiente de una recta cuando solo se conoce un punto, voy a calcular la ecuación de la recta que pasa por el punto (1; -3) conociendo el valor de la pendiente.

Calcular la ecuación de la recta utilizando la ecuación punto-pendiente

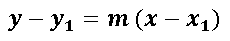
El valor de m=2 y las coordenadas del punto 1 es (X1; Y1)

Por lo que la ecuación de la recta se calcula como sigue:

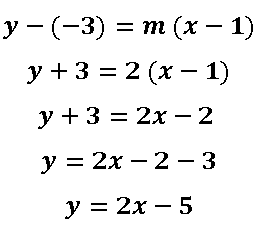
Para generar las coordenadas del otro punto de la recta 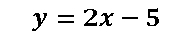voy a sustituir x=0 en la ecuación de la recta quedando de la siguiente manera:

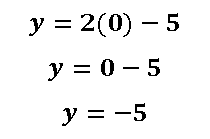
Habiendo sustituido x=0 en la ecuación de la recta nos da que y= -5, por lo que las coordenadas del segundo punto es (0; -5)

Cálculo de la pendiente de la recta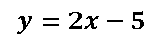conociendo los puntos (1; -3) y (0; -5)

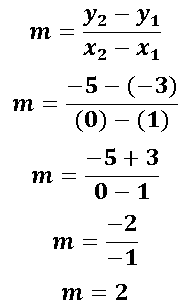
Explicación del análisis demostrativo del ejercicio planteado

Como podemos darnos cuenta la recta cuya ecuación es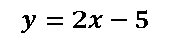 y que es tangente a la función cuadrática 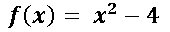en el punto (1 ; -3) se le puede encontrar el valor de la pendiente simplemente derivando la función cuadrática y sustituyendo la coordenada en x del punto tangencial, dándonos como resultado que la pendiente (m) es igual a 2.

Para corroborar este valor de la pendiente de la recta tangencial quise encontrar el valor de la pendiente conociendo dos puntos, para este caso uno de los puntos es el tangencial (1 ; -3) y el otro punto lo conseguimos de la ecuación de la recta que se consiguió de la herramienta que nos brinda la geometría analítica en la que se puede conseguir la ecuación de la recta conociendo un punto y su pendiente, dándonos como resultado un valor de la pendiente (m) igual que cuando lo hicimos por la derivada.

Gráfico de la función cuadrática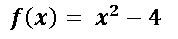y la recta tangencial 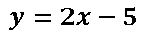en el punto (1; -3) utilizando el software geogebra 5.0

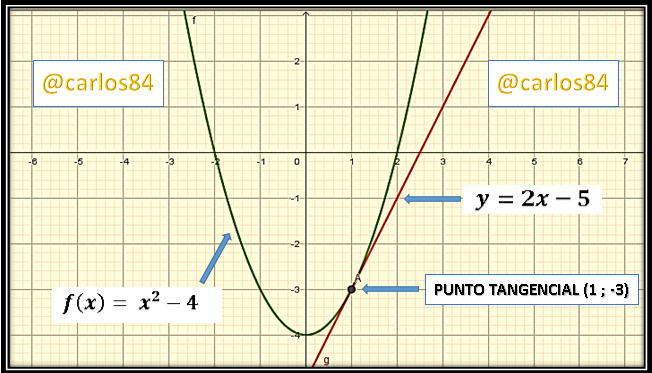
Entre los aspectos que se pueden considerar de este gráfico es que la función cuadrática es una función polinómica de variable real, tiene simetría con el eje Y. Corta al eje X en 2 y -2 y al eje Y en -4.

Lo otro que se puede observar es que claramente tiene un punto tangencial de coordenadas (1; -3), no está demás aclarar que para la generación del gráfico utilice el software geogebra 5.0, realizando luego un capture de pantalla y editando la imagen con las herramientas de diseño de Microsoft Word 2011.

Conclusiones y aportes educativos en esta publicación

1. Lo más claro y realmente convincente es que el ejercicio # 7 del capítulo II propuesto por el libro de Cálculo volumen I del autor Larson en la página 104 nos puede llevar como en este caso a demostrar que la pendiente de una recta que es tangente a cualquier curva en un punto dado se puede calcular mediante la derivada de una función real y luego ser corroborada aplicando la ecuación de la geometría analítica para calcular la pendiente de una recta conociendo dos puntos.

2. Con la resolución de este ejercicio cualquier alumno a nivel universitario puede sacar sus propias conclusiones y análisis referente a la necesidad existente que pudo haber surgido en los tiempos remotos en los que Isaac newton y Leibniz trabajaron para descubrir lo que hasta los momentos yo en lo particular considero es una de las herramientas más importante del cálculo infinitesimal como lo es la Derivada de una función real.

3. Otra herramienta muy importante para poder realizar deducciones y comparaciones son los gráficos que se puedan generar de este tipo de ejercicios, en este caso utilice como herramienta para generar el gráfico el software geogebra 5.0 de uso libre. En este gráfico se puede apreciar claramente el punto tangencial por donde pasa la recta a la parábola en el punto (1; -3), incluso se pueden elegir otros puntos arbitrarios pertenecientes a la recta para calcular nuevamente la pendiente de la recta y darnos cuenta que el valor de la pendiente de esta recta siempre nos dará el valor de m=2.

Referencia consultada y recomendada

Nota: Todas las imágenes en este artículo son de mi autoría y fueron elaboradas utilizando las herramientas de diseños de Microsoft Word y Microsoft PowePoint 2011.