Teorema del Valor Medio: Demostración y Aplicación /// Mean Value Theorem: Demonstration and Application

El Teorema del Valor Medio se le atribuye a Joseph-Louis Lagrange, un físico, matemático y astrónomo nacido en Turín (Italia) el 25 de enero de 1736, y quien murió en París el 10 de abril de 1813, este teorema es considerado por algunos matemáticos como el más importante del cálculo.

---

he Mean Value Theorem is attributed to Joseph-Louis Lagrange, a physicist, mathematician and astronomer born in Turin (Italy) on January 25, 1736, and who died in Paris on April 10, 1813, this theorem is considered by some mathematicians as the most important theorem of calculus.

---

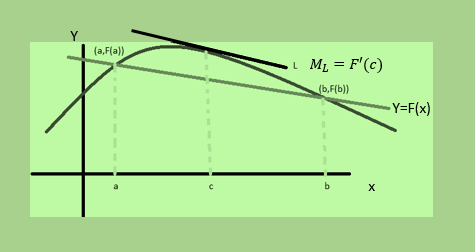
El Teorema del Valor Medio dice lo siguiente:

Si F(x) es una función continua en un intervalo [a,b] y diferenciable en (a,b) entonces existe c en (a,b) tal que F(a)- F(b)= F’(c)(b-a)

---

The Mean Value Theorem states the following:

If F(x) is a continuous function on an interval [a,b] and differentiable in (a,b) then there exists c in (a,b) such that F(a)- F(b)= F'(c)(b-a).

---

Vamos a demostrar este Teorema usando el Teorema de Rolle. //
Let's prove this Theorem using Rolle's Theorem.

---

Comencemos // Let's start

---

Definamos una nueva función: // Let's define a new function:

---

---

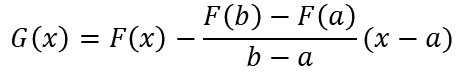
La función G(x) es la suma algebraica de dos funciones polinómicas, por ello cumple con las condiciones del Teorema de Rolle, es decir, continua en [a, b] y diferenciable en (a, b)

---

The function G(x) is the algebraic sum of two polynomial functions, so it satisfies the conditions of Rolle's Theorem, i.e., continuous in [a, b] and differentiable in (a, b).

---

Verifiquemos si G cumple con las condiciones del Teorema de Rolle.
Esto es: F(a)-F(b)=0

---

Let us verify if G satisfies the conditions of Rolle's Theorem.
That is: F(a)-F(b)=0

---

Para ello desarrollemos // To this end, let us develop

---

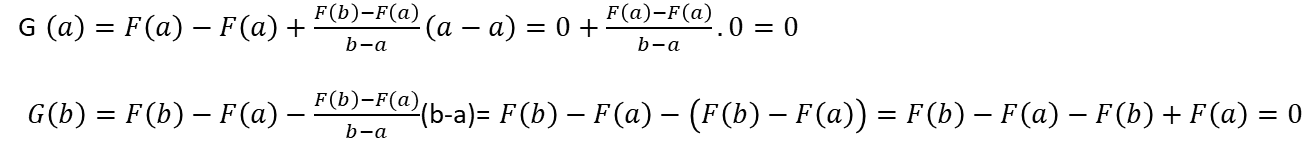
Entonces, de acuerdo al Teorema de Rolle, existe un c en (a,b) tal que F’(c)=0

Then, according to Rolle's Theorem, there exists a c in (a,b) such that F'(c)=0

---

Para encontrar a c debemos, primero, desarrollar G’(x)

To find c we must, first, develop G'(x)

---

Para lograr esto, tomaremos en cuenta que al derivar

In order to achieve this, we will take into account that when deriving

---

---

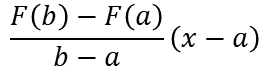
Nos resulta

We find it

---

---

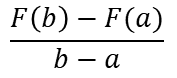
Luego

Then

---

---

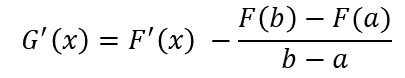
Con lo cual, hemos demostrado el teorema.

Thus, we have proved the theorem.

---

Ejercicio
Usando el Teorema del Valor Medio, verifique que:

Using the Mean Value Theorem, verify that:

a)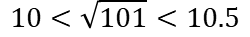

---

b)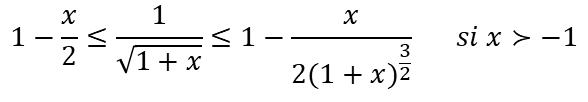

---

Solución a:

Solution a:

---

Definamos la siguiente función :

Let us define the following function:

---

---

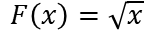
Esta función es continua en el intervalo (10, 10.5) y diferenciable en el intervalo [10, 10.5]

This function is continuous on the interval (10, 10.5) and differentiable on the interval [10, 10.5]

---

Veamos la gráfica a continuación

Let's see the graph below

---

---

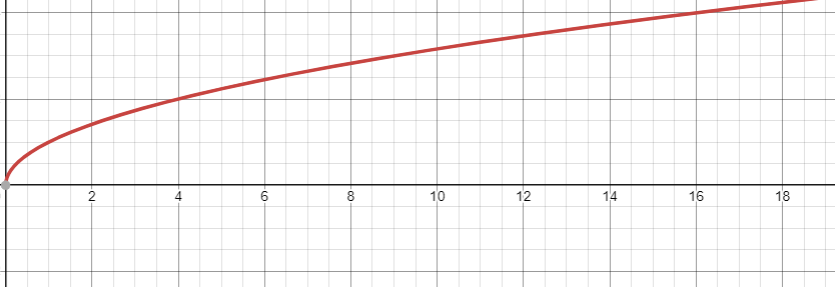
Por lo tanto, de acuerdo al Teorema del Valor Medio, debe existir un c en (10, 10.5) tal que:

Therefore, according to the Mean Value Theorem, there must exist a c in (10, 10.5) such that:

---

---

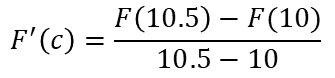
Derivando a F se tiene que:

Deriving F we have that:

---

---

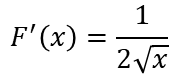
Sustituyendo a x por c en la derivada de F e igualando se obtiene lo siguiente:

Substituting x for c in the derivative of F and equating, we obtain the following:

---

---

---

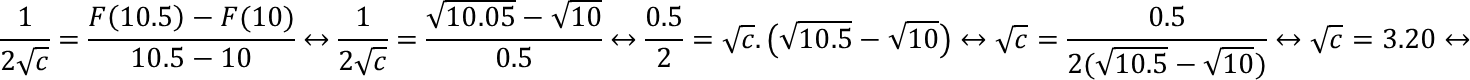
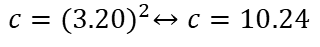
Con lo cual llegamos al resultado esperado.

This leads us to the expected result.

---

Dejamos el ejercicio b pendiente al lector.

We leave exercise b open to the reader.

---

▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄

---

Créditos

El post es totalmente original de la autora.
Algunos conceptos se desarrollaron con el apoyo de los Textos:
‘'Cálculo Diferencial para Administración y Economía’'. Autor es Jorge Sáenz. Segunda Edición. Editorial Hipotenusa. Barquisimeto-Venezuela. 2007.
"Calculo Diferencial e Integral". Autores: Howard E. Taylor y Thomas L. Wade. Editorial Limusa. Mexico. 1974.
Para la gráfica nos apoyamos en la Calculadora Gráfica Desmos, Paint y PowerPoint.

Credits

The post is entirely original by the author.
Some concepts were developed with the support of the Texts:
''Differential Calculus for Management and Economics''. Author is Jorge Sáenz. Second Edition. Hipotenusa Publishing House. Barquisimeto-Venezuela. 2007.
"Differential and Integral Calculus". Authors: Howard E. Taylor and Thomas L. Wade. Editorial Limusa. Mexico. 1974.
For the graphing we used Desmos Graphing Calculator, Paint and PowerPoint.

Posted with STEMGeeks