OPERACIONES CON POLINOMIOS/ADICIÓN Y SUS PROPIEDADES.

Comencemos con la adición de polinomios, la cual es una operación que cumple con las propiedades de: conmutatividad, asociatividad, existencia del elemento neutro y del opuesto o simétrico.
La adición de polinomios se define así:
Dados los polinomios:
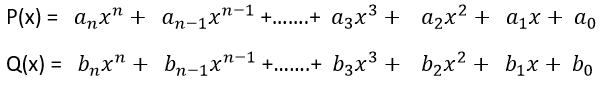
Entonces:
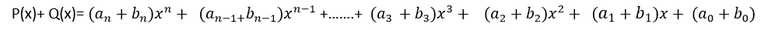
Donde el polinomio suma tendrá el grado del polinomio sumando que tenga mayor grado o el mismo grado de los sumandos si estos tienen el mismo grado.
Primer ejemplo:
Dados los polinomios:
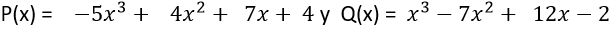
Hallar P(x)+ Q(x)
Observe que ambos polinomios tienen el mismo grado 3, entonces el grado de P(x)+ Q(x) también es 3.
Veamos:
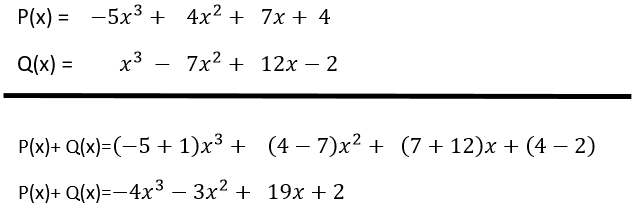
Segundo ejemplo:
Dados los polinomios:
Observe que el polinomio P(x) tiene grado 3 y Q(x) también es 2, entonces el grado de P(x)+ Q(x) es 3.
Veamos:
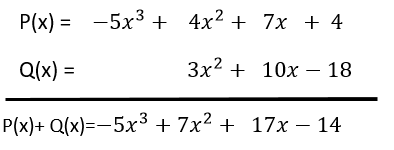
En cuanto a las propiedades de la adición de polinomios, podemos afirmar que:
Es muy sencillo probar que P(x)+ Q(x)= Q(x)+ P(x), ya que la adición de polinomios es conmutativa. El lector podrá validar estos resultados con cualquier ejemplo.
Verifiquemos la propiedad asociativa.
Consideremos los siguientes tres polinomios:
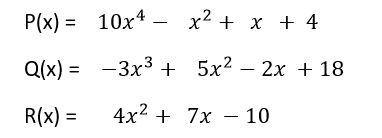
Queremos verificar que [P(x)+Q(x)]+R(x)= P(x)+[Q(x)+R(x)]= [P(x)+R(x)]+Q(x)
Comencemos con:
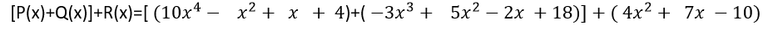
Primero resolvemos las operaciones que se encuentran agrupadas dentro del corchete; en este caso, eliminamos los paréntesis y reducimos los términos semejantes, es decir sumaremos los monomios de igual grado:
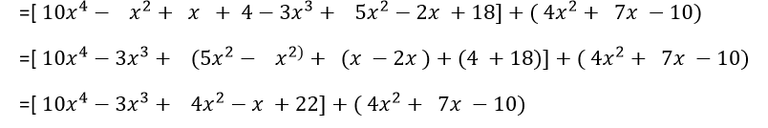
Eliminamos los signos de agrupación; es decir, corchetes y paréntesis:
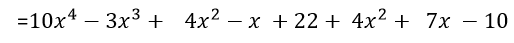
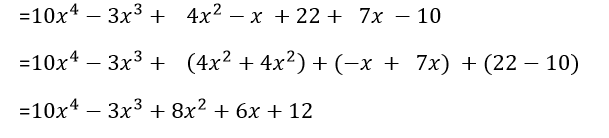
Siguiendo este mismo modelo, el lector podrá verificar que:
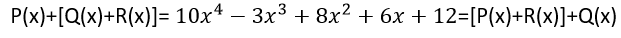
Elemento neutro
Existe un polinomio que llamaremos O(x) tal que para cualquier polinomio P(x)+O(x)=O(x)+P(x)
Tal polinomio es el POLINOMIO NULO
El Polinomio Nulo es un polinomio cuyos coeficientes son todos iguales a 0; es decir, O(x)=0
Existencia del OPUESTO O SIMETRICO.
Para todo polinomio P(x) existe un polinomio –P(x) tal que: P(x)+[-P(x)]=-P(x)+P(x)=O(x)
Ilustremos con un ejemplo:
Consideremos el siguiente polinomio:
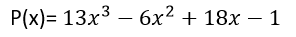
Entonces
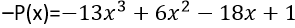
De tal forma verificamos que:
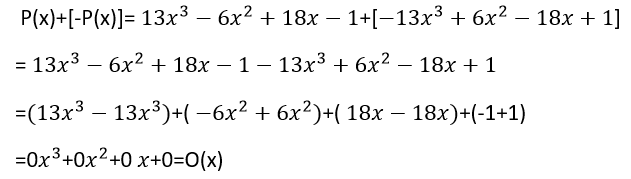
Hasta aquí la adición de polinomios y sus propiedades, esperamos que haya dentro de la comunidad alguien a quien le sea de utilidad este post.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.