FUNCIONES E IDENTIFICACIÓN DE VARIABLES EN EL CONTEXTO DE LA ECONOMÍA///FUNCTIONS AND IDENTIFICATION OF VARIABLES IN THE CONTEXT OF THE ECONOMY
The situations that arise in the field of business (accounting administration and economics) follow certain rules where the relationship that exists between the different variables is expressed in terms of dependence generated by a determinism or causality between them; said causality will always be defined by the number of variables that interact in the dynamic process that is being studied.
In these situations, mathematics plays a fundamental role as a tool to interpret and understand these processes, since through it it is possible to order and express these rules through mathematical models, for this it is essential to identify the variables and their relationships of dependency, which will give a global idea of the problem.
Un ejemplo sencillo que permite recrear las ideas anteriores es el siguiente:
A simple example that allows you to recreate the previous ideas is the following: In a factory the cost of production in raw material y of certain merchandise will depend on the quantity x of merchandise produced. It is clear that y depends on x. But the dependency relations are not enough since it is necessary to know the rule that relates or links them (for which we use mathematics).
Comencemos:
Let's get started:
In the previous example, to know the cost of production y, you would have to multiply the cost of producing a single item by the number of items produced x. If it costs the manufacturer $ 15 to produce an item, then the relationship is expressed by the following rule: y = 15x. According to her, producing 5 items costs the manufacturer 15.5 = 75; this is $ 75. F. See figure.
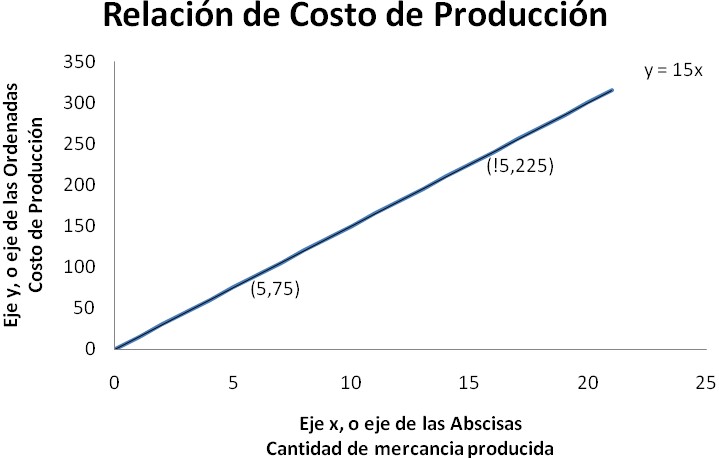
The way of expressing that the cost of production of 5 units of the item corresponds to $ 75 is observed in the graph as an ordered pair (5, 75). There are some concepts that are prerequisites for understanding the concept of function, which have already been mentioned in the previous example, they are:
Para ordenado.
En general cuando se habla del par ordenado (x,y) se entiende que y es una variable que depende x mediante alguna regla. La definición de regla se da a continuación.
Regla.
Es el conjunto de procedimientos matemáticos que permiten obtener el valor de una variable dependiente y a partir de una variable independiente x.
Ejercicio de aplicación:
Identificar las variables independiente y dependiente y luego graficar cada una de las siguientes expresiones.
a) z= 2w + 4
b) a – 3 =b
c) -5= r – t
d) Y= 2x +1
e) g) x2 + y2= 1
f) h) y= x3
Ordered pair.
In general, when talking about the ordered pair ( x, y ), it is understood that y is a variable that depends x by means of some rule . The definition of rule is given below.
Rule.
It is the set of mathematical procedures that allow obtaining the value of a dependent variable y from an independent variable x.
Application exercise:
Identify the independent and dependent variables and then graph each of the following expressions.
a) z = 2w + 4
b) a - 3 = b
c) -5 = r - t
d) Y = 2x +1
e) x2 + y2 = 1
f) y = x3
Definición de función.
Una función es una regla que asocia a cada variable independiente x, una única variable dependiente y.
Actividad: Cuáles de las reglas del ejemplo anterior cumple con la definición de función?
Prueba de la recta vertical:
Una regla representa a una función, si al trazar sobre su gráfico una recta vertical ésta la toca en un solo punto.
Actividad:
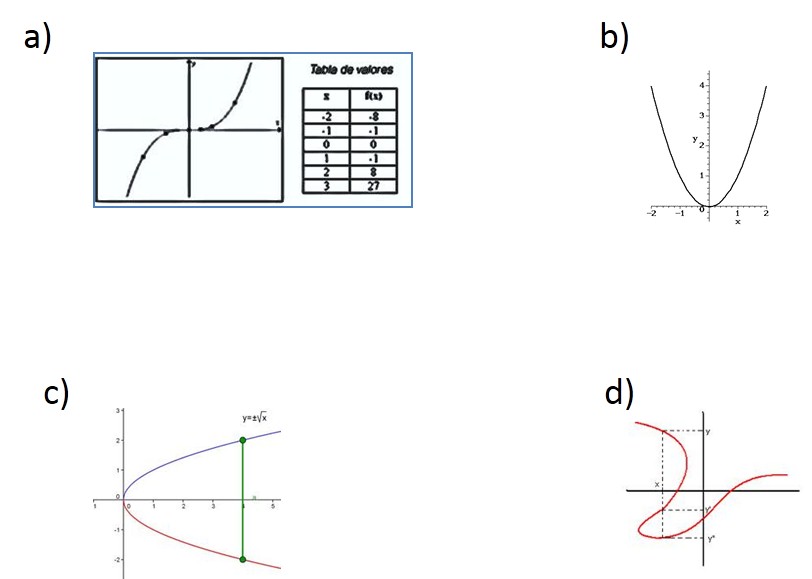
Cuáles de los siguientes gráficos representan a una función:
Definition of function.
A function is a rule that associates to each independent variable x, a single dependent variable y.
Activity:
Which of the rules in the previous example meets the definition of a function?
Test of the vertical line:
A rule represents a function, if when drawing a vertical line on its graph, it touches it at a single point.
Activity:
Which of the following graphs represent a function:
Notación funcional: y= F(x)
Ejemplos:
Sea f la función definida por f(x)= 5x + 6
Halle f(3), f(-3), f(a), f(-a), y f(a+1)
Sea s la función definida por s(t) =2t2/√(t-1)
Halle: s(2), s(a), s(t+1) s(1) y s(t-1)
Sea f(x)=√x
Halle: f(0), f(1), f(4), f(x+1), f(x2 -9)
Functional notation: y = F (x)
Examples:
Let f be the function defined by f (x) = 5x + 6
Find f (3), f (-3), f (a), f (-a), and f (a + 1)
Let s be the function defined by s (t) = 2 2 / √ (t-1)
Find: s (2), s (a), s (t + 1), s(1) and s (t-1)
Let f (x) = √x
Find: f (0), f (1), f (4), f (x + 1), f (x2 -9)
Referencia/Reference
TAN, SOO (2005). MATEMÁTICA PARA ADMINISTRACIÓN Y ECONOMÍA. 3º EDICIÓN. CENGAGE LEARNINGEDITORES.

Su post ha sido valorado por @ramonycajal