Es posible que a causa de la tecnología actual, no seamos tan conscientes de las dificultades que los matemáticos atravesaban hace miles de años. Quizás para ellos representaba simplemente un reto como cualquier otro y no algo tedioso, dado el conocimiento y tecnología disponible para la época.

^{Newton - Pixabay}

Desde hace miles de años, civilizaciones antiguas tenían alguna noción del número "π", desde el antiguo Egipto hasta el Imperio Chino. Este número también hace cierta aparición indirecta en la Biblia.

Pero el cálculo de este número en épocas antiguas o bien era algo impreciso o se llevaba a cabo mediante métodos que hoy en día serían vistos como extremadamente tediosos y complejos. Recordemos que "π" representa la división entre el perímetro y el diámetro de una circunferencia.

^{John Reid, CC BY-SA 3.0, via Wikimedia Commons}

Aproximadamente 250 años antes de Cristo, Arquímedes realizó el cálculo de "π" con un método sumamente largo, pero que al menos brindaba una precisión aceptable incluso hoy día, situando a π entre 3.1408 y 3.1429.

El método de Arquímedes se puede apreciar con mayor detalle en los primeros minutos del siguiente video:

En pocas palabras, antiguamente se intentó primero dividir el perímetro de un hexágono inscrito en un círculo entre el diámetro del círculo. El resultado sería claramente 3. Pero un cuadrado exterior al círculo daría un resultado para π de 4 (3<π<4).

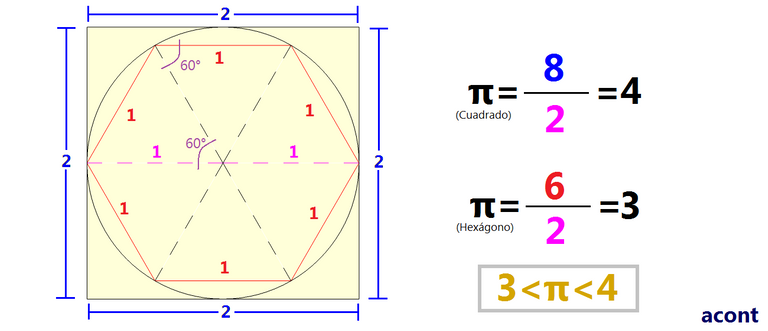
Luego, Arquímedes incrementó los lados del polígono interno al doble, conformando un dodecágono. También realizó un dodecágono externo al círculo. Con los diámetros de estos dos dodecágonos, obtuvo un rango de 3.106<π<3.215.

Arquimedes incrementa el número de lados del polígono hasta llegar a 96. De esta manera, se llega al rango ya mencionado de 3.1408<π<3.1429.

^{Método de Arquímedes. !Original: FredrikVector: Leszek Krupinski, Public domain, via Wikimedia Commons}

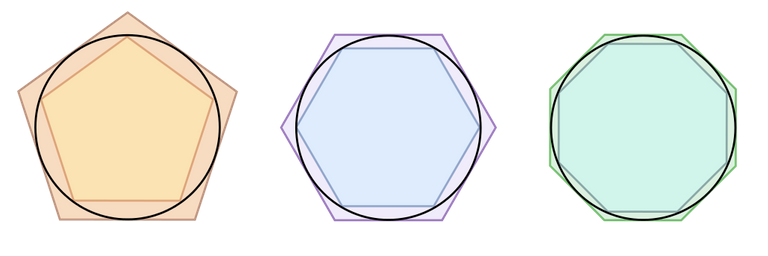
Este número se siguió calculando así por muchos siglos después. En el Siglo XVII el matemático holandés Ludolph van Ceulen realizó este mismo cálculo con un polígono de 2⁶² lados. Esto le llevó a calcular los primeros 35 decimales de π, algo impresionante para aquella época, pero poco práctico el día de hoy.

Imagino que lograr este nivel de precisión para π en el Siglo XVII conllevaría meses o incluso años de cálculos. Algo que solo un matemático haría por el amor al arte y a la ciencia.

Pero nadie más volvería a utilizar este método cuando Isaac Newton calculó π utilizando el cálculo, teoría que el mismo había desarrollado. Esto solo requería unas cuantas líneas escritas en un papel, y quizás algunos días extra si quieres obtener una alta precisión en los decimales de "π".

Método de Newton

Isaac Newton, durante la cuarentena originada por un rebrote de la peste bubónica en el año 1666, empezó a experimentar con el triángulo de Pascal, y la fórmula que nos permite obtener los coeficientes de una expresión desarrollada a partir del Teorema del Binomio. Esta expresión nos dice que podemos encontrar estos coeficientes sin tener que desarrollar el Triángulo de Pascal, con solo saber el número "n", es decir, la potencia del binomio.

Sin embargo, la regla general para aplicar esta ecuación es que "n" debe de ser un número entero. Newton quiso poner a prueba la ecuación, utilizando como "n" números negativos, e incluso números decimales o fracciones.

El principal interés de Newton estaba en n=1/2, tal como veremos más adelante. Sin embargo, tanto para números negativos como para números fraccionarios, la serie se vuelve infinita. Para n=1/2 resulta:

Por otro lado, la ecuación que representa a una circunferencia de radio 1 centrada en un plano de coordenadas (X,Y) es X²+Y²=1, donde si despejamos la variable Y, obtenemos la ecuación Y=(1-X²)^1/2.

Aquí es donde podemos evidenciar que el binomio (1-X²)^1/2 se puede igualar a la serie infinita obtenida mediante n=1/2. La única diferencia es que ahora sustituiremos X por -X²:

Aquí es donde Newton aplica el cálculo infinitesimal, teoría que el mismo acababa de desarrollar. El integraría ambos lados de la igualdad.

La serie infinita, ahora integrada, representa el área bajo la curva en la circunferencia. Pero este integral se definiría de 0 a 1, por lo que el área en cuestión sería una cuarta parte del círculo de radio 1.

Sabemos que un círculo posee un área de πr², pero siendo r=1 el radio de nuestro círculo, su área total es π. Pero al integrar de 0 a 1 estamos tomando en cuenta el área por encima del eje "X" de ese rango, siendo esta área una cuarta parte del área total, es decir, π/4.

La serie infinita integrada de 0 a 1 se iguala a π/4. Luego se despeja π y se evalua el resultado para los límites establecidos. Obtuvimos así un valor cercano a π, teniendo en cuenta que solo tomamos 5 términos de la serie infinita:

La precisión de π dependerá de cuanto nos extendamos en la serie. Pero Newton no se conformó con esto, y vio la posibilidad de llegar más rápido a un resultado más preciso, cambiando los límites de integración.

En vez de integrar de 0 a 1, el límite superior se establece en 1/2. Como resultado, el área de interés ya no será π/4, sino que habrá que emplear algo de geometría para hallarla:

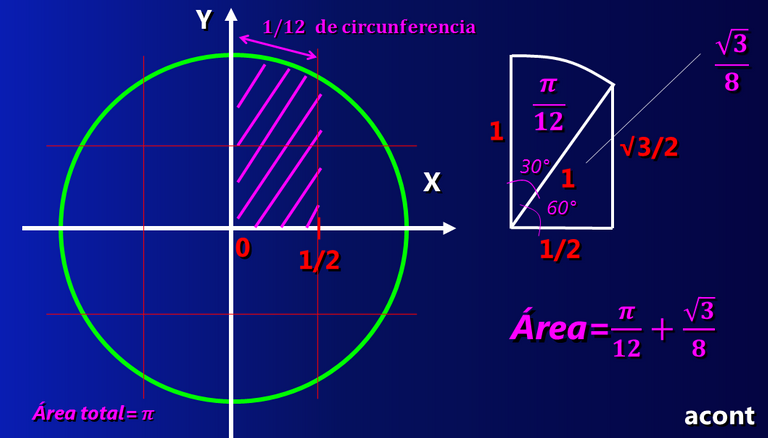
Esta nueva área, se iguala a la nueva integral. Como resultado, el despeje de π nos lleva a una ecuación que converge más rápidamente que la anterior hacia un resultado más preciso, por lo que se requieren menos términos de la serie para una precisión similar a la anterior serie.

Utilizando 6 términos de la serie infinita, hemos obtenido 5 decimales correctos para π.

En conclusión, vemos como pueden surgir nuevas maneras de realizar algo con mucho menor esfuerzo y tiempo, a través de nuevas perspectivas y teorías, como lo fue en este caso el cálculo infinitesimal. La manera en que tradicionalmente se realiza algo, puede ser mejorada a través del conocimiento científico y la experimentación. Esto lo ha demostrado Isaac Newton, quien encontró una manera más eficiente de calcular una constante matemática que sigue siendo objeto de estudio hasta el día de hoy.

Referencias

•Número π — Wikipedia

•La ridícula forma en la que se calculaba Pi... Hasta que... — Veritaseum en Español

---

Imágenes de autoría propia realizadas mediante SketchUp y PowerPoint.

Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.

---

¡Gracias por visitar! — ¡Thanks for visiting! @acont